Метод прогонки для розв’язання слар

Розглянемо систему 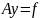, де А – трьох діагональна матриця, тобто в ній відмінними від нуля є елементи тільки головної і двох побічних діагоналей.

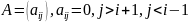
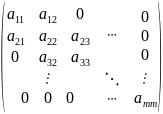
Систему прийнято записувати

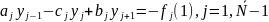
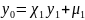
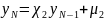(2)

Такі системи з 3-х діагональними матрицями розв’язуються методом прогонки: полягає в послідовнім виключенні невідомих.

Вивід розрахункових формул методом прогонки

Розвязок будемо шукати у виді

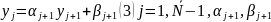– невідомі коефіцієнти.

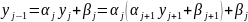
Підставимо 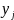і 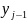у рівняння (1)

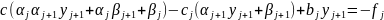
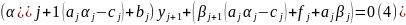
Тоді рівняння (4) буде виконуватись, якщо 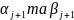будуть виражатися таким чином, щоб вирази в дужках дорівнювали нулю.

(5)

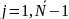
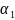
Рівняння (5) представляє собою лінійне різницеве рівняння 1-го порядку, тоді для їх розвязку необхідно задати початкові дані, тобто 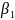. початкові значення 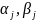вибираємо з еквівалентності умов (2)і (3), тоді 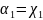, . Визначення за рпрогоночні коефіцієнти івностю (5) і знаходження цих коефіцієнтів називається прямою прогонкою. Коли є знайдені, тоді розвязок системи шукається у виді (3) коли , 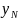- будемо шукати із еквівалентності (2) та із системи (3) при j=1.

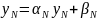
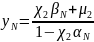(7)

Така процедура називається зворотною (оберненою) прогонкою. Метод прогонки застосовується коли знаменник у (5) , (7) не дорівнюють нулю, тобто коли матриця А є 3-х діагональна з діагональним переважанням.

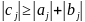
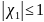
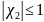
Ітераційні методи розв’язання слар

Ax=f

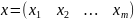
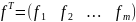
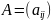
В ітераційних методах розвязок будемол шукати з певною заданою точністю

Ітераційний метод Якобі

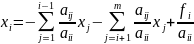(2)

Якщо верхній індекс сумування менший ніж нижній то сума =0.

Ітераційний метод Якобі: 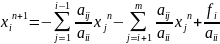(3)

Де 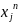- і-ва компонента розвязку на n-вій ітерації

- вектор початкового наближення

Кількість виконаних ітерацій буде визначатись або фіксованим значенням n, яке задається користувачем або ж виконанням певної умови: 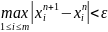- дана умова э умовою завершення ітераційного процесу.

Ітераційний метод Зейделя

Ітераційний метод Зейделя виражається:

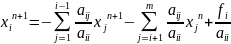(4)

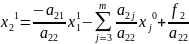
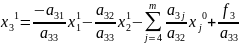
Для знаходження і-вої компоненти на n+1 – ій ітерації ми використовуєм і-1 компоненту поточної ітерації і m-(i-1)=m-i+1 компонент попередньої ітерації.

Для дослідження стійкості методів краще записувати у матричній формі

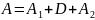
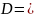
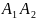- нижня і верхня трикутна матриця з нулями на головній діагоналі. Систему (2) можемо записати у вигляді

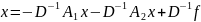
Ітераційний процес у матричній формі може бути записаний і виражатиме метод Якобі:

(5)

Метод Зейделя:

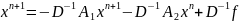(6)

Запишемо ці методи у зручній для користувача формі. Рівність (5) домножимо на D.

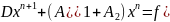
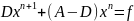
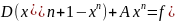(7)

(7) – еквівалентна форма методу Якобі. Показує, що якщо ітераційний метод Якобі є збіжний, то він збігається до розв’язку початкової системи.

Рівність (6) домножимо на D.

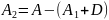
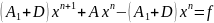
(8)

Якщо метод Зейделя є збіжним, тоді він збігається до розвязку початкової системи.

Для покращення швидкості збіжності в ітераційнім процесі вводять деякі числові параметри, які можуть залежати від номера ітерації:

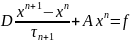
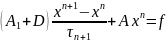
Вибір таких ітераційних параметрів впливає на збіжність методів, і такі ітераційні параметри вибирають за двома умовами:

1. При якому параметрі метод є збіжним

2. При яких значеннях параметра метод збігається якнайшвидше

Методи, в яких використовуються більше ніж одна ітерація називаються багатокроковими.

k – кроковий метод може виражатись через рівність