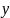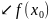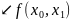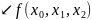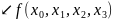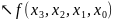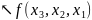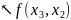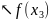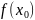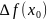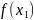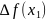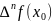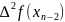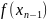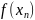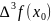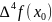Властивості розділених різниць

1. Розділена різниця суми (або різниці) функцій дорівнює сумі розділених (або різниці) розділених різниць

2. Сталий множник можна винести за знак розділеної різниці

3. Розділені різниці є симетричними відносно своїх аргументів

Побудова інтерполяційного многочлена Ньютона

Є деяка функція визначена на [a,b] тоді ми виберемо деяку точку , яка не співпадає з вузлами інтерполяції. Побудуємо першу розділену різницю:

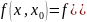
(2)

Запишемо розділену різницю другого порядку

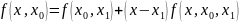
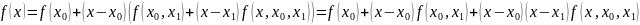
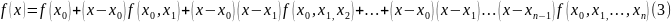
Сукупність правої частини (3) многочлен 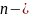го порядку

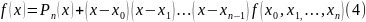
Покладаючи в рівності (4) 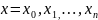одержимо рівняння

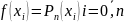
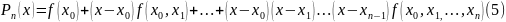
(5) – інтерполяційний многочлен Ньютона

Другий доданок у рівності (4) називається залишковим членом і він представляє собою істинну похибку процесу інтерполяції

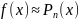
Інтерполяційний многочлен (5) називається інтерполяційний многочлен Ньютона для інтерполяції вперед. Він використовується якщо нам необхідно знайти наближення значень функції в точці яка є близькою до точки . Інтерполяційний многочлен Ньютона може бути одержаний з інтерполяційного многочлена Лагранжа простим перегрупуванням. На відміну від многочлена Лагранжа в якому кожен член залежить від усіх вузлів інтерполяції. Будь-який член многочлена Ньютона залежить тільки від перших вузлів інтерполяції. Таким чином додавання вузлів у (5) не потребує перерахунку попередніх членів.

Якщо вузли впорядковано 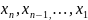то аналогічно ми можемо одержати формулу Ньютона

Даний інтерполяційний многочлен використовується коли необхідно знайти значення функції який знаходиться ближче до правого краю проміжку .

Приклад

	0	1	2	3
	-1	0	2	3
	0	1	21	88

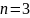
-1	0
		1
0	1		3
		10		4
2	21		19
		67
3	88

Для інтерполяції вперед підставимо в (5)

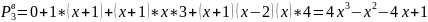
Для інтерполяції назад підставимо в (6)

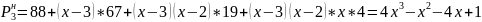
Скінченні різниці

Нехай на проміжку [a,b] задане деяке рівномірне розбиття , тобто введена рівномірна сітка 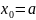; ; 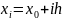; відомі значення функції.

у замалих вузлах , де тоді різниці записані у вигляді

. . . . . . . . . .

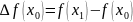
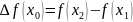
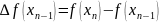
називаються скінчинними різницями 1-го роду.

. . . . . . . . . .

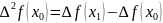
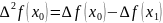
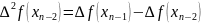
називаються скінченними різницями 2-го роду.

Скінченні різниці n-го порядку:

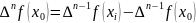
Скінченні різниці зручно зображати у такому трикутному вигляді:

…	…			…
		…
		∆

Скінченні і розділені різниці зв’язані за наступними співвідношеннями:

(1)

Доведення проведемо методом математичної індукції:

; ;

;

.

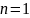
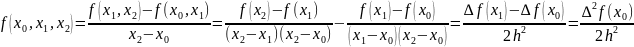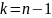
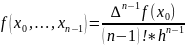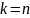
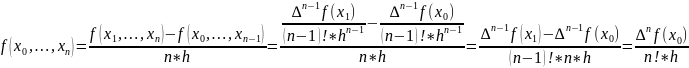Отже, рівність (1) зв’язує розділені і скінченні різниці, тоді підставимо цей зв'язок у 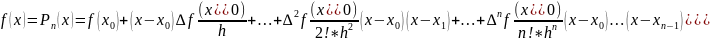(2).

. (2)

(3) інтерполяційний многочлен Ньютона для рівновіддалених вузлів.

Заміна змінної :

;

;

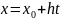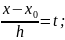
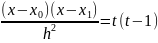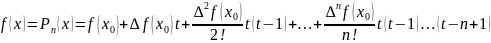. (3)

Так,як при записі многочлена Ньютона порядок вузлів не є важливим, то ми можемо записати інтерполяційний многочлен Ньютона для інтерполяції назад ввівши заміну змінної:

; ;

;

;

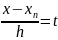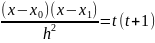; (4)

(4) – формула інтерполяційного многочлена Ньютона у випадку рівномірно віддалених вузлів.

Формулу (4) використовують для знаходження наближеного значення функції, яка є близька до .

		1 3 17 67	2 14 50
-1	0			12 36
0	1
1	4				24
2	21
3	88

;

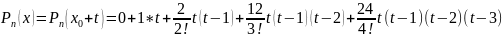Побудова многочлена Ньютона для інтерполяцій назад:

;

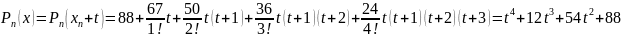Побудова інтерполяційного многочлена Ньютона через розділені різниці для функції:

		1 3 17 67	1 7 25
-1	0			2 6
0	1
1	4				1
2	21
3	88

;
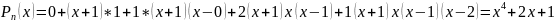