Інтерполяційний многочлен Ерміта

Нехай у вузлах інтерполяції , 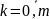де вибирається з деякого проміжку 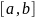і вузли інтерполяції є різними, , .

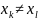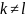Задані значення функції для кожного вузла , та задані значення похідних , порядком .

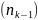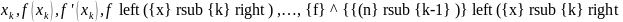
Всіх відомих значень є для вузла інтерполяції.

Тоді потрібно побудувати алгебраїчний многочлен степеня n, де 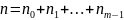, для якого в одночас будуть виконуватись:

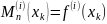, , (1)

Такий многочлен, який задовольняє рівняння (1) називається інтерполяційний многочлен Ерміта.

Він буде мати вигляд:

Для відшукання коеф нам потрібно розв’язати лінійну алгебраїчну систему, яка випливає із рівності (1).

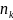̶ назив кратністю вузла .

Число рівнянь системи (1) = .

Збіжність інтерполяційних процесів

При побудові кожного інтерполяційного многочлена виникає питання, чи буде збігатися до 0 похибка інтерполяції, якщо кількість вузлів необмежено збільшувати?

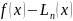, при .

При збільшенні вузлів інтерполяції не завжди похибка 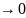, але якщо за вузли інтерполяції взяти корені многочлена Чебешева 1-го роду, то інтерполяційний процес може бути збіжним.

Означення(збіжності інтер. процесу).

Множину вузлів з проміжку , які є впорядкованими

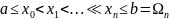
До цих пір ми розглядали скінченні сітки, які складалися з скінченної кількості вузлів. Тепер розглянемо множину точок, у якої кількість вузлів буде зростати:

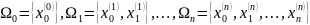
Нехай функція є визначеною і неперервною на проміжку . Тоді можемо задати послідовність інтерполяційних многочленів , побудованих для функцій , по x значення .

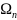Інтерполяційний многочлен є збіжним в точці 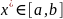, якщо виконується .

Рівномірна збіжність має місце, якщо .

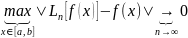Властивість збіжності буде щалежати від двох факторів:

1. Від вибору сіток інтерполяції;

2. Від гладкості функції, яку ми наближаємо.

Теорема.

Якщо функція є нескінченне число разів диференційованою і всі її похідні обмежені на , , , , 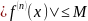тоді 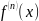– збігається рівномірно до на .

Теорема(Фабера).

Якою б не була послідовність сіток, знайдеться така функція на проміжку , що послідовність інтерполяційних многочленів 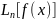не збігається рівномірно до функції на цьому проміжку.

Теорема(Марцікевича).

Якщо функція є неперервна на , то можемо підібрати таку послідовність сіток, для якої інтерполяційний многочлен буде збігатися рівномірно на заданому проміжку.

Як наслідок:

Якщо функція є цілою функцією, тобто її можна представити у виді 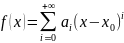то послідовність буде рівномірно збігатися до функції на .

Інтерполяція сплайнами

Означення.

Для того, щоб побудувати на якийсь інтерполяційний многочлен, цей проміжок розбивають на частинні відрізки і функцію на кожномуз відрізків записують многочленом не високого порядку.

Означення.

Сплайном називають кусково поліноміальну функцію, яка визначається на , яка має на цьому проміжку деяке визначене число неперервних похідних.

Означення.

Сплайном 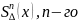порядку з дефектом ладкості 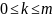на називається функція, яка на кожному із проміжків є многочленом степеня не вищого ніж :

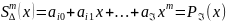(1)

Цей поліном повинен задовольняти умові неперервних похідних до 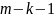порядку:

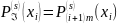(2)

Обов’язкова умова інтерполяційної функції:

, (3)

Побудуємо сплайн 1-го порядку:

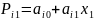(4)

Необхідно, щоб виконувалась умова близькості функції до сплайна

,

Для відшукання невідомих коефіцієнтів на проміжку 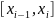розв’язується система:

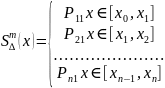
Найбільше вживані є сплакни при .

+
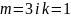