
- •Обчислювальний експеримент. Теорія попиту.
- •Абсолютна і відносна похибки
- •Методи розв’язання системи лінійних рівнянь (слр). Прямі методи слр.
- •Метод Гауса чисельного розв’язку слр.
- •Вивід розрахункових формул
- •Модифікація методу Гауса
- •Умови застосування методу Гауса і його зв'язок з розкладом матриці на множники.
- •Обчислення визначника
- •Обчислення обернених матриць
- •Обумовленість с-ми лінійних рівнянь Стійкість слар
- •Обумовленість слар, число обумовленості
- •Метод прогонки для розв’язання слар
- •Ітераційні методи розв’язання слар
- •Ітераційний метод Якобі
- •Ітераційний метод Зейделя
- •Канонічна форма однокрокових ітераційних методів
- •Приклад розв’язання методом Зейделя та Якобі
- •Метод простої ітерації
- •Дослідження збіжності ітераційних методів
- •Необхідна і достатня умова збіжності у стаціонарних методах
- •Оцінки швидкості збіжності стаціонарних ітераційних методів
- •Многочлени Чебишева 1-го роду і многочлени Чебишева на відрізку [0,1]
- •Многочлен Чебишева на проміжку [a,b]
- •Ітераційні методи Чебишовським набором параметрів
- •Неявний Чебишевський ітераційний метод
- •Інтерполяція функцій
- •Інтерполяційний многочлен Лагранжа
- •Розділені різниці. Інтерполяційний многочлен Ньютона
- •Властивості розділених різниць
- •Побудова інтерполяційного многочлена Ньютона
- •Приклад
- •Скінченні різниці
- •Формула залишкового члена інтерполяційного многочлена Лагранжа
- •Інтерполяції за допомогою раціональних функцій
- •Інтерполювання періодичних функцій
- •Інтерполяційний многочлен Ерміта
- •Збіжність інтерполяційних процесів
- •Інтерполяція сплайнами
Канонічна форма однокрокових ітераційних методів
Доцільно
ввести деякий єдиний запис ітераційного
методу. Канонічною формою одно крокових
ітераційних методів системи (1) будем
називати запис, де
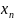 - розвязок на n-
ій ітерації
- розвязок на n-
ій ітерації
 (9)
(9)
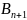 - матриця яка
визначає той чи інший ітераційний метод,
- матриця яка
визначає той чи інший ітераційний метод,
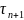 – ітераційний параметр.
– ітераційний параметр.
Припустимо,
що введемо деяке початкове наближення ,
тоді існує матриця
,
тоді існує матриця
 .
Тоді з рівняння (9) у нас можуть бути
визначені послідовно
, тоді для
знаходження
.
Тоді з рівняння (9) у нас можуть бути
визначені послідовно
, тоді для
знаходження
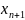 достатньо
розв’язати таку систему рівнянь у
матричній формі
достатньо
розв’язати таку систему рівнянь у
матричній формі

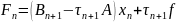
Ітераційний
процес буде називатися нестаціонарним,
якщо параметри будуть вибиратися окремо.
Якщо
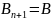 ,
,
 , то такий
проуес називається стаціонарним.
, то такий
проуес називається стаціонарним.
Якщо
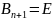 ,
то такий процес називається явним
ітераційним методом.
,
то такий процес називається явним
ітераційним методом.
Приклад розв’язання методом Зейделя та Якобі

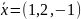 - точний розвязок.
- точний розвязок.
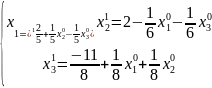
Методом
Якобі: 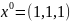 - початкове
наближення
- початкове
наближення



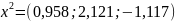
Методом Зейделя: - початкове наближення


Порівнявши виконані операції на обох методах дійшли висновку, що метод Зейделя збігається швидше ніж метод Якобі.
Метод простої ітерації
Метод
простої ітерації – це явний стаціонарний
метод з сталими параметром
 .
.
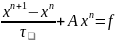 (10)
(10)
Якщо ж параметр буде змінний то одержимо метод Річадсона (11)
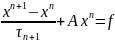 (11)
(11)
Для ітераційних методів (10) і (11) є відомий метод вибору параметрів та в тому випадку коли матриця А є симетрична і додатньовизначена
Узагальненим
метод Зейделя (8) є метод з введеним
парметром
 і може бути записаний
і може бути записаний
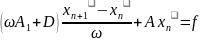 (12)
(12)
Такий
метод (12), де
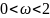 носить назву верхньої релаксації. Введем
розрахункові формули для методу (12)
носить назву верхньої релаксації. Введем
розрахункові формули для методу (12) 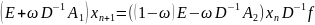
Запишемо метод верхньої релаксації в координатній формі
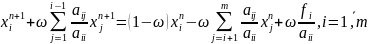
Дослідження збіжності ітераційних методів
Розглянемо
систему Ax=f
(1) із не
виродженою дійсною матрицею А і одно
кроковий стаціонарний метод, процес
може бути записаний у виді (2)
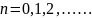 .
.
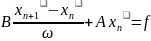 (2) де
(2) де
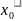 - задане початкове наближення
- задане початкове наближення
Будемо
говорити що ітераційний метод (2) є
збіжним якщо
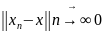 .
Під нормою
вектора будемо розуміти середньоквадратичну
норму
.
Під нормою
вектора будемо розуміти середньоквадратичну
норму
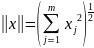 , де
, де
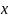 елемент m
–
вимірного векторного простору H
із заданим
скалярним добутком
елемент m
–
вимірного векторного простору H
із заданим
скалярним добутком
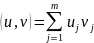 , u,v
, u,v
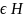
При
дослідженні збіжності будемо
використовувати деякі матричні
нерівності. Для дійсної матрисі С
нерівність
 означає що
означає що
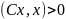 ,
,
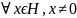 .
Тоді з
випливає
параметр
.
Тоді з
випливає
параметр
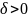 ,
що
,
що
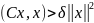 ,
якщо
і С – симетрична матриця, тоді всі її
власні значення є додатніми, і тоді в
якості
,
якщо
і С – симетрична матриця, тоді всі її
власні значення є додатніми, і тоді в
якості
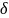 ми можемо вибрати min
з цих власних значень . якщо
і С – не симетрична, тоді
ми можемо вибрати min
з цих власних значень . якщо
і С – не симетрична, тоді
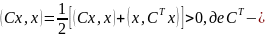 транспонована до С і тоді за
беремо min
власне
значення
транспонована до С і тоді за
беремо min
власне
значення
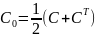 Із оцінки
випливає що
Із оцінки
випливає що
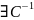 .
Якщо
.
Якщо
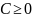 ,
тоді
,
тоді
 ,
то
,
то
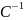 може і не існувати ю
може і не існувати ю
Похибка
розв’язання системи (1) методом (2) на
n-ій
ітерації
може бути записана
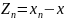 .
Підставивши
похибку у рівняння (2)
.
Підставивши
похибку у рівняння (2)
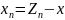
 (3)
(3)
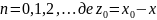
Тоді справедлива теорема
Теорема 1
Нехай
А–симметрична додатньовизначена
матриця
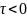 і нехай виконується
і нехай виконується
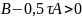 ,(4)
тоді ітераційний метод (2) є збіжним.
,(4)
тоді ітераційний метод (2) є збіжним.
Доведення.
Достатньо показат, що середньоквадратична
норма розвязку
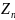 рівння (3)
рівння (3)
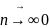 при будь-якому початковому наближенні
при будь-якому початковому наближенні
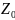 .
Для цього спочатку покажемо, що при
виконанні умови (4) послідовність
.
Для цього спочатку покажемо, що при
виконанні умови (4) послідовність
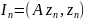 являєтья
не зростаючою, тоді із рівняння (3) можемо
записати
являєтья
не зростаючою, тоді із рівняння (3) можемо
записати

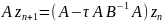

Так
як матриця А за умовами теореми є
симетричною
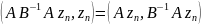 ,
тоді попередню нерівність можемо
переписати
,
тоді попередню нерівність можемо
переписати

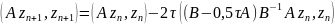 (5)
(5)
Тоді
враховуючи нерівність (4)
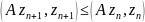 .
Таким чином послідовність
.
Таким чином послідовність
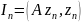 є монотонною і обмеженою знизу нулем і
є монотонною і обмеженою знизу нулем і
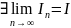 (6). Із додатньої визначеності матриці
(6). Із додатньої визначеності матриці
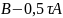 випливає існування константи
випливає існування константи
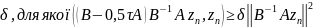 ,
тоді із рівності (5) одержимо нерівність
,
тоді із рівності (5) одержимо нерівність
 ,
перейшовши до границі при і врахувавши
рівність (6) бачимо що
,
перейшовши до границі при і врахувавши
рівність (6) бачимо що
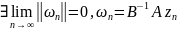 . врахувавши що матриця А є додатньовизначеною
і відповідно оборотною
. врахувавши що матриця А є додатньовизначеною
і відповідно оборотною
 .
З останньої нерівності
.
З останньої нерівності
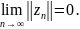 Доведено.
Доведено.
Наслідок 1.
Нехай
матриця А –додатньовизначена і симетрична
з діагональною перевагою, тобто для неї
виконується така нерівність
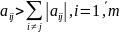 (7) , тоді метод Якобі є збіжним.
(7) , тоді метод Якобі є збіжним.
Доведення.
Умова збіжності (4) у даному випадку
матиме вигляд
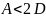 . покажемо,
що така матрична нерівність випливає
із нерівності (7). Запишемо квадратну
форму
. покажемо,
що така матрична нерівність випливає
із нерівності (7). Запишемо квадратну
форму
 .
Скориставшись оцінками для квадратичної
форми
.
Скориставшись оцінками для квадратичної
форми
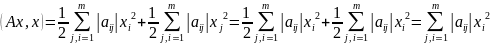
так
як матриця А – симетрична і додатньовизначина,
то

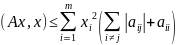 (8), тоді (7) можна
записати
(8), тоді (7) можна
записати
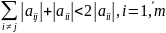 і тоді (8)
запишеться
і тоді (8)
запишеться
 (9)
(9) 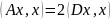
Остання
оцінка еквівалентна умові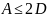 .
Доведено.
.
Доведено.
Наслідок 2
Нехай матриця А і додатньовизначена і симетрична, тоді метод верхньої релаксації
збігається при умові .
Відповідно метод
Зейделя збігається при
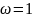 .
.
Доведення .
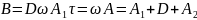
Із
симетричності матриці А
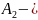 транспонована
для
транспонована
для
 ,
тому
,
тому
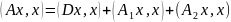 .
Умова (4) прийме вигляд
.
Умова (4) прийме вигляд
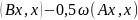 =
враховуючи попередні рівності можемо
записати
=
враховуючи попередні рівності можемо
записати
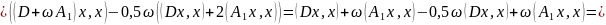
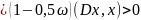
Виконання такої нерівності можливе, якщо
Наслідок. Теорема (необхідна і достатня умова збіжності методу простої ітерації )
 (10)
(10)
Для
того щоб ітераційний процес (10) був
збіжним необхідно і досить, щоб
 (11)
(11)
Доведення
Достатність.
Для того, щоб ітераційний процес був
збіжним достатньо щоб виконувалось (4)
і тоді
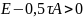 (12), тоді умова (12) еквівалентна тому, що
всі власні значення матриці
(12), тоді умова (12) еквівалентна тому, що
всі власні значення матриці
 повинні бути додатніми. Нехай матриця
A
має власні
значення
повинні бути додатніми. Нехай матриця
A
має власні
значення
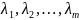 тоді
тоді
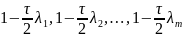 є власними значеннями
. тоді
найменшим серед цих власних значень
є власними значеннями
. тоді
найменшим серед цих власних значень
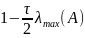 , цього достатньо, щоб вон обуло
, цього достатньо, щоб вон обуло
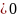 і тоді
звідки
випливає (11)ю
і тоді
звідки
випливає (11)ю
Необхідність.
Покажемо, що нерівність (11) є необхідною
умовою для збіжності (10). Припустимо, що
нерівність (11) порушена, тоді знайдеться
деяке початкове наближення
,для
якого
 при
при
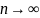 .
Покажемо це, припустимо
.
Покажемо це, припустимо
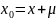 , де
- точний
розвязок системи (1) а
, де
- точний
розвязок системи (1) а
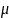 - власний вектор матриці А, що відповідає
- власний вектор матриці А, що відповідає
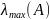 , тобто
, тобто
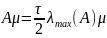 тоді при виборі початкового наближення
похибка
тоді при виборі початкового наближення
похибка
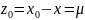 .
Тоді з
формули (10)
.
Тоді з
формули (10)
 .
.
Припустимо,
що
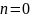 ,
,
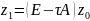
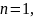
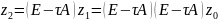
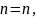
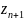 =
=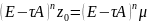
Враховуючи,
що
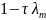 є власними значеннями
є власними значеннями
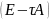 можемо записати
можемо записати
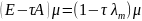 , тоді
, тоді
 .
.
Враховуючи
властивості норми
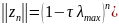
Якщо
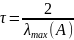 тоді
тоді
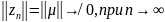
Якщо
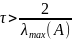 тоді
тоді
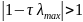 ,
,

Таким чином умова є необхідною умовою для збіжності ітераційного методу (10).
