8.Криволинейный интеграл 2го рода и его выч

Если существует предел (не зависящий от способа составления интегральных сумм)

,

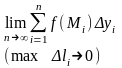то он называется криволинейным интегралом по координате y от функции f(M) по ориентированной кривой АВ(L) (КРИ-2) и обозначается так:

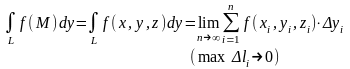
Если вдоль кривой AB(L) на плоскости 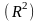определены две функции и 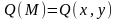и существуют интегралы

,

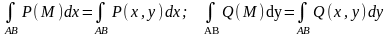то их сумму называют КРИ-2 (общего вида)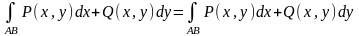 (2) на плоскости .

Криволитнейный интеграл II рода (КРИ-2) (общего вида) в пространстве 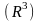называют выражением вида

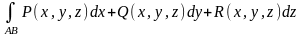(3)

Основные свойства КРИ-2.

1.

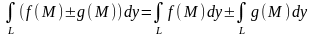
2.

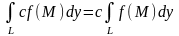
3. 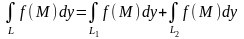, если кривая разбита на две част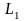и и 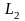и движение по этим частям установлено в том же направлении, как и по всей кривой.

4. Если направление движения по L(AB) изменить на противоположное (двигаясь от В к А), то знаки всех проекций 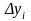в интегральной сумме (1) меняются на противоположные и поэтому .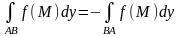

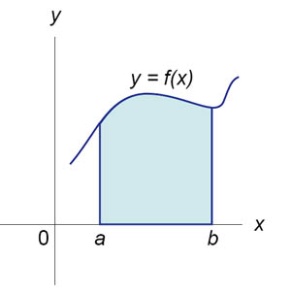
9.Вычисление площади области ограниченной прямой

Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на[a, b], то

Площадь криволинейной трапеции

Площадь фигуры, ограниченной осью 0x, двумя вертикальными прямыми x = a, x = b и графиком функцииf (x) (рисунок 1), определяется по формуле

Рис.1		Рис.2

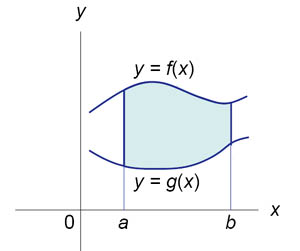
Пусть F (x) и G (x) - первообразные функций f (x) и g (x), соответственно. Если f (x) ≥ g (x) на замкнутом интервале [a, b], то площадь области, ограниченной двумя кривыми y = f (x), y = g (x) и вертикальными линиями x = a, x = b (рисунок 2), определяется формулой

10.Касательная плоскости и нормаль к поверхности

Пусть поверхность   задана уравнением

                                    (1)

в неявном виде. Будем считать, что   и в некоторой окрестности точки   функция   имеет непрерывные частные производные, одновременно не равные нулю. Тогда

                 (2)

Мы пишем   вместо  .

Для определенности предположим, что  . Тогда на основании теоремы о неявной функции  существует окрестность точки  , в которой поверхность   описывается явно непрерывно дифференцируемой функцией  . Уравнение касательной плоскости к   в точке  , как мы знаем, имеет вид ,где

.

В силу этого уравнения касательной плоскости к   в точке   запишется так:

,                (3)

а уравнение нормали к   в точке   - так:

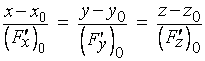.                                   (4)

Те же уравнения (3), (4) мы получим, если предположить, что   или  . В этих случаях в окрестности   поверхность   описывается явно соответственно уравнениями

.

Мы видим, что при условии (2) поверхность   в любой точке   имеет касательную плоскость, непрерывно изменяющуюся при непрерывном передвижении точки  . Такую поверхность называют гладкой поверхностью  .

Другое дело, если  . В этом случае нельзя гарантировать, что в точке   существует касательная плоскость к  . Она может существовать, а может и не существовать.