46.Тригонометрический ряд Фурье

Если f(x) разлагается на отрезке   в равномерно сходящийся тригонометрический ряд:

 (1)

,то это разложение единственное и коэффициенты определяются по формулам:

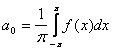
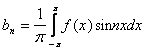 , где n=1,2, . . .

Тригонометрический ряд (1) рассмотренного вида с коэффициентами называется тригонометрическим рядом Фурье, а    коэффициентами ряда Фурье.

47. Разложение в ряд Фурье 2l – периодичных функций

Если   – четная,  -периодическая, то ее ряд Фурье принимает вид:

 

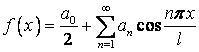;                                (1.37)

 

;

 

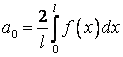;                                  (1.38)

 

 ,  .

Таким образом, четная функция, удовлетворяющая условиям теоремы Дирихле , раскладывается в ряд Фурье только по косинусам.

Если   – нечетная,  -периодическая, то ее ряд Фурье принимает вид:

 

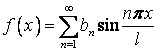;                                       (1.41)

 

;

 

;                                               (1.42)

 

.

Таким образом, нечетная функция, удовлетворяющая условиям теоремы Дирихле, раскладывается в ряд Фурье только по синусам.

48. Ряд Фурье для четных и нечетных функций

Пусть функция   – четная,  -периодическая, удовлетворяет условию теоремы Дирихле 1.1. Тогда ее ряд Фурье в действительной форме (1.21) в точках непрерывности имеет вид

 

,                                    (1.35)

 

так как, согласно формулам (1.33), (1.34), коэффициенты Фурье (1.22) преобразуются к виду:

;

;

;

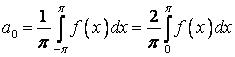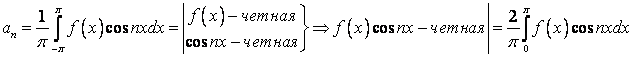т. е.

;

 

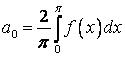;                                     (1.36)

Пусть функция   – нечетная,  -периодическая, удовлетворяет условию теоремы Дирихле 1.1. Тогда ее ряд Фурье в действительной форме (1.21) в точках непрерывности имеет вид

 

,                                      (1.39)

 

так как, согласно формулам (1.33), (1.34), коэффициенты Фурье (1.22) преобразуются к виду:

;

;

;

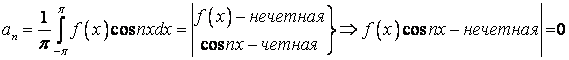т. е.

;

 

;                                               (1.40)

 

49. Разложение в ряд Фурье непериодических функций

Предположим, что функция удовлетворяет условиям Дирихле на каждом отрезке из 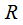и 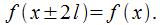Для того, чтобы разложить ее в тригонометричский ряд, необходимо преобразовать этот случай в случай периодической функции с периодом , осуществляя замену , поскольку

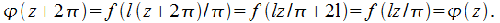
В этом случае 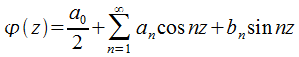, здесь

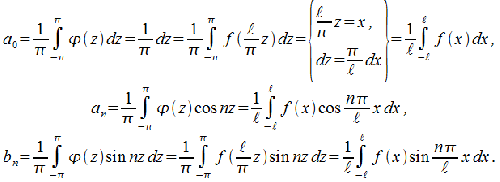
Итак,

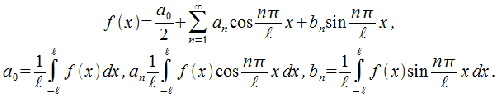
50. Комплексная форма ряда Фурье

Пусть функция f (x) определена в интервале [−π, π]. Применяя формулы Эйлера

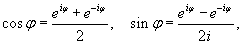
можно записать ряд Фурье данной функции в комплексной форме:

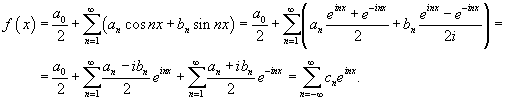
Мы использовали здесь следующие обозначения:

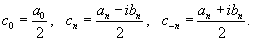
Коэффициенты cn называются комплексными коэффициентами Фурье. Они определяются формулами

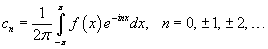
Если нужно построить продолжение функции f (x), имеюшей произвольный период 2L, то соответствующее выражение в комплексной форме имеет вид:

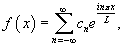
где

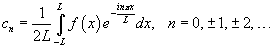
Комплексная форма ряда Фурье алгебраически проще и более симметрична. Поэтому, она часто используется в физике и прикладных расчетах.

51. Преобразование Фурье

Если f(x) – любая абсолютно интегрируемая на всей числовой оси функция, непрерывная или имеющая конечное число точек разрыва первого рода на каждом отрезке, то функция

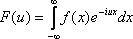
называется преобразованием Фурье функции f(x).

Функция F(u) называется также спектральной характеристикой функции f(x).

Если f(x) – функция, представимая интегралом Фурье, то можно записать:

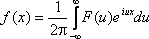
Это равенство называется обратным преобразованием Фурье

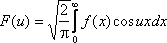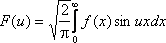Интегралы и называются соответственно косинус - преобразование Фурье и синус – преобразование Фурье.

Косинус – преобразование Фурье будет преобразованием Фурье для четных функций, синус – преобразование – для нечетных.

Преобразование Фурье применяется в функциональном анализе, гармоническом анализе, операционном исчислении, теории линейных систем и др.