38.Формулы для вычисления радиуса сходимости степенного ряда. Свойства степенных рядов.

33.Формулы для вычисления R.

; ;

; ; ;

; , ;

; ; ; ;

; R –не измен. При почленном диффиренцировании

; ;

; имеет место сходи абс (-R;R); то ст. ряд. Сх . прав. На (-r;r)

-сх;

;

; ;

;

;

39.Ряд Тейлора –

это ряд вида

Ряд Маклорена- это частный случай ряда Тейлора, когда а=0:

Будем рассматривать ситуацию когда ряд Тейлора сходиться

Разложения в ряд Маклорена некоторых функций

40. Разложения в ряд Маклорена ех

Как оно получилось? По формуле Маклорена: Рассмотрим функцию  , тогда:

Теперь начинаем находить производные в точке ноль: первую производную, вторую производную, третью производную и т.д.  Это просто, поскольку при дифференцировании экспонента превращается в саму себя:

И так далее….

Совершенно очевидно, что 

Подставляем единицы в формулу Маклорена и получаем наше табличное разложение!

Аналогично можно вывести некоторые другие табличные разложения (но далеко не все выводятся именно так).

41. Разложения в ряд Маклорена некоторых функций

Биномиальный ряд

с интервалом сходимости -1<х<1. При m натуральном ряд превращается в многочлен степени m (разложение бинома Ньютона). При m>0 ряд сходится также на границах интервала сходимости, т. е. при х=±1; при -1<0 ряд сходится на правой границе и расходится на левой; при m<-1 ряд расходится на обеих границах.

Частные случаи биномиального ряда:

(убывающая геометрическая прогрессия);

42. Разложения в ряд Маклорена некоторых функций

Применим интегральную формулу

Разложение  может быть осуществлено в соответствии с (30.13) при В этом случае

 

 

при этом для ряда характерна абсолютная расходимость на промежутке Если , получаем , что представляет собой гармонический расходящийся ряд, при ряд предполагает условную сходимость.

43.Примерение рядов для постр решений ду

Пусть необходимо найти решение у(х) задачи Коши для дифференциального уравнения 2-го порядка:

Ищем у(х) в виде ряда Тейлора:

 (30.14)

Значения известны, поэтому определяется

сразу Для нахождения следующих коэффициентов ряда (30.14) необходимо брать последовательно производные от   и подставлять в них известные уже значения предыдущих производных.

44.Прим рядов для вычисл определ интеграла

С помощью степенных рядов возможно интегрировать дифференциальные уравнения ,Рассмотрим линейное дифференциальное уравнение вида:

Если все коэффициенты и правая часть этого уравнения разлагаются в сходящиеся в некотором интервале степенные ряды, то существует решение этого уравнения в некоторой малой окрестности нулевой точки, удовлетворяющее начальным условиям.

Это решение можно представить степенным рядом:

Для нахождения решения остается определить неизвестные постоянные c_i. Эта задача решается методом сравнения неопределенных коэффициентов. Записанное выражение для искомой функции подставляем в исходное дифференциальное уравнение, выполняя при этом все необходимые действия со степенными рядами (дифференцирование, сложение, вычитание, умножение и пр.)

Затем приравниваем коэффициенты при одинаковых степенях х в левой и правой частях уравнения. В результате с учетом начальных условий получим систему уравнений, из которой последовательно определяем коэффициенты c_i.

45. Ур-е Бесселя. Ф-я Бесселя

уравнение Бесселя(1)

Это линейное дифференциальное уравнение второго порядка с переменными коэффициентами играет большую роль в приложениях математики. Функции, ему удовлетворяющие, называются бесселевыми, или цилиндрическими, функциями.  Будем искать решение уравнения Бесселя (4) в виде ряда:  .  Тогда  ,  ,  ,  .  Следовательно, приходим к требованию  или к бесконечной системе уравнений              ,  которая распадается на две системы:  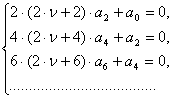                            Первая из них удовлетворится, если взять  … Во второй системе   можно взять произвольно; тогда  … однозначно определяются (если   не является целым отрицательным числом). Взяв   ,  найдем последовательно:  ,  ,  ,  и в качестве решения уравнения (4) получим ряд:  Этот ряд, формально удовлетворяющий уравнению (4), сходится для всех положительных значений   и, следовательно, является решением уравнения (4) в области   (в случае целого   в области ).  Функция                                                                           (5)  называется бесселевой функцией первого рода с индексом  . Она является одним из решений уравнения Бесселя (4). В случае целого неотрицательного индекса   получим: