
- •1.Таблица производных
- •Элементарные функции
- •2.Таблица интегралов
- •3.Тройной интеграл его вычисление
- •4. Замена переменной в тройном интеграле
- •7. Криволинейный интеграл 1го рода и его вычисление
- •8.Криволинейный интеграл 2го рода и его выч
- •9.Вычисление площади области ограниченной прямой
- •10.Касательная плоскости и нормаль к поверхности
- •11. Поверхн. Интеграл 1го рода
- •12.Поверхностный интеграл 2го рода и его выч
- •13.Д,у. Осн понятия. Задача Коши
- •14.Ду с разделяющимися переменными
- •15.Однородные уравнения
- •16.Линейные ду 1го порядка.Метод подстановки Бернули
- •Метод Бернулли
- •17 Метод вариации произвольного постоянного
- •18.Уравнение Бернули
- •19.Ду в полных дифференциалах
- •20.Ду высших порядков. Задача Коши
- •21.Ду допускающее понижение порядков
- •22.Определитель Вронского.Структура решения неоднор ду
- •23.Лин однор ду с пост коэф
- •24.Линейные неоднор ду.Метод Лагранжа
- •25.Лин неоднорДу с пост коэф
- •26. Числовой ряд. Сумма ряда
- •30.Радикальный признак коши
- •33. Знакопеременные
- •36.Теоремы о дифференцировании
- •38.Формулы для вычисления радиуса сходимости степенного ряда. Свойства степенных рядов.
- •40. Разложения в ряд Маклорена ех
- •41. Разложения в ряд Маклорена некоторых функций
- •42. Разложения в ряд Маклорена некоторых функций
- •43.Примерение рядов для постр решений ду
- •44.Прим рядов для вычисл определ интеграла
- •46.Тригонометрический ряд Фурье
- •47. Разложение в ряд Фурье 2l – периодичных функций
- •48. Ряд Фурье для четных и нечетных функций
- •49. Разложение в ряд Фурье непериодических функций
- •50. Комплексная форма ряда Фурье
- •51. Преобразование Фурье
- •52. Ряд Фурье по полной замкнутой системе ортогональной функции
- •53. Понятие о функции комплексной переменной
- •54. Дифференцируема функция комплексного переменного
1.Таблица производных
Пусть
в некоторой окрестности
точки
![]() определена
функция
определена
функция
![]() Производной
функции f
в точке x0
называется предел,
если он существует,
Производной
функции f
в точке x0
называется предел,
если он существует,
![]()
Общепринятые обозначения производной функции y = f(x) в точке x0:
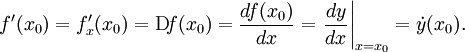
Производная
функции
![]() и
сама является функцией - она определяется
значением
и
сама является функцией - она определяется
значением
![]() в
точке
в
точке
![]() .
Эта функция обозначается символом
.
Эта функция обозначается символом
![]() или
.
или
.
Элементарные функции
1 |
(C)'=0 |
2 |
(xα)'=αxα-1 |
3 |
(1x)'=-1x2 |
4 |
(x)'=12x |
5 |
(logax)'=1xlogae |
6 |
(lnx)'=1x |
7 |
(ax)'=axlna |
8 |
(ex)'=ex |
9 |
(sinx)'=cosx |
10 |
(cosx)'=-sinx |
11 |
(tgx)'=1cos2x |
12 |
(ctgx)'=-1sin2x |
13 |
(arcsinx)'=11-x2 |
14 |
(arccosx)'=-11-x2 |
15 |
(arctgx)'=11+x2 |
16 |
(arcctgx)'=-11+x2 |
Правила вычисление производныx
Производная суммы двух функций:
![]()
Производная произведения постоянной и функции:
![]()
Производная произведения двух функций:
![]()
Производная частного двух функций:
![]()
Производная сложной функции:
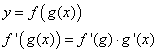
Производная
функции вида
![]() :
:
![]()
2.Таблица интегралов
Функция F(x), определенная в промежутке (а,b), называется первообразной данной функции f(x) в этом промежутке, если для любого значения хЄ(а,Ь) выполняется равенство F'(x) = f(x).
Неопределенным
интегралом от данной функции f(x) называется
множество всех ее первообразных:![]() dx=F(x)+C,где F'(x) = f(x).Знак
dx=F(x)+C,где F'(x) = f(x).Знак ![]() называется знаком неопределенного
интеграла, функция f(x) - подынтегральной
функцией, выражение f(x)dx - подынтегральным
выражением.
называется знаком неопределенного
интеграла, функция f(x) - подынтегральной
функцией, выражение f(x)dx - подынтегральным
выражением.
Операция нахождения первообразной данной функции называется интегрированием.

3.Тройной интеграл его вычисление
Пусть
в некоторой пространственной области
(V)
задана функция f(x,y,z).
Разобьем эту область на конечное число
частей
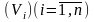 ,
имеющих соответственно объемы
,
имеющих соответственно объемы
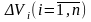 .
В пределах i-го
элемента
.
В пределах i-го
элемента
 выбираем точку
выбираем точку
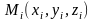 ,
значение функции в этой точке
,
значение функции в этой точке
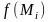 умножим на
умножим на
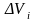 ,
получим интегральную сумму
,
получим интегральную сумму
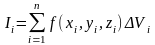 .
.
Если
предел интегральной суммы существует
при неограниченном увеличении n
(т.е.
 ,
то его называют тройным интегралом от
функции f(x,y,z)
по области V
и обозначают
,
то его называют тройным интегралом от
функции f(x,y,z)
по области V
и обозначают
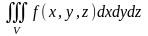 (или
(или
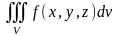 ).
).
Таким образом, по определению имеем
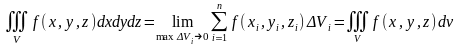 (1)
(1)
Тройной интеграл (1) существует, если:
функция f(x,y,z) ограничена;
функция f(x,y,z) непрерывная;
ограниченная функция f(x,y,z), все разрывы которой лежат на конечном числе поверхностей с объемом 0.
Существование и величина тройного интеграла не зависит от значений, принимаемых функцией вдоль конечного числа поверхностей с объемом 0.
Если
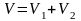 ,
то
,
то
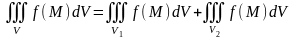 ,причем
из существования интеграла
,причем
из существования интеграла
слева следует существование справа, и обратно.
Если в области V интегрируемы две функции f(M) и g(M), то интегрируема функция
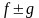 ,
причем
,
причем
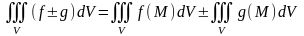
Если интегрируема в (V) функция f удовлетворяет неравенству
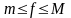 ,
то
,
то
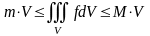
Теорема о среднем. Если f(x,y,z) непрерывна в (V), то
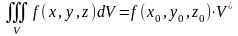 ,
,
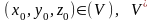 –
объем тела V.
–
объем тела V.
