6) Властивість диференціювання зображення

Якщо оригінал , то , , також оригінал і

7) Властивість інтегрування зображення

Якщо оригінал і інтеграл збігається,

то .

7.2 Зображення згортки

Нехай маємо дві функції і , Згорткою цих функцій називається інтеграл (якщо він існує). Цей інтеграл є функцією від і позначається .

Якщо і є оригіналами, то із означення оригінала випливає, що . Неважко переконатися, що .

Властивість згортки

Якщо оригінали і , то

Таблиця зображень і оригіналів

Використовуючи перетворення Лапласа, а також властивості зображень, складаємо таблицю (7.1)

Таблиця 7.1 – оригінали і відповідні їм зображення

№	Оригінал	Зображення
1	1
2
3

Продовження таблиці 7.1

4
5
6
7
8
9
12
13
14
15
16
17

Продовження таблиці 7.1

18
19
20

7.3 Схема побудови розв’язку диференційного рівняння з частинними похідними

Наведемо схему побудови розв’язку диференційного рів-няння з частинними похідними, де шукана функція за-лежить лише від двох змінних і . Нехай вона задовольняє рівняння:

, (7.2)

де – неперервні функції від , задані на проміжку . Нехай треба знайти розв’язок рівняння (7.2) для напівнескінченної смуги: , , що задово-льняє задані додаткові умови

П.У.

К.У. (7.3)

де – сталі.

Задача (7.2) – (7.3) нестаціонарна, оскільки шуканий роз-в’язок істотно залежить від початкових умов і описує так званий неусталений перехідний режим фізичного процесу.

Застосуємо перетворення Лапласа до функції за змінною . Вважаємо, що функції , і є оригіналами. Позначивши зображення шуканої функції через , запишемо наступні співвідношення:

, , .

Тут розглядається як параметр.

Для знаходження зображень частинних похідних по за-стосуємо теорему про диференціювання оригіналу. Одержимо

,

.

Вважатимемо, що – оригінал, тоді крайові умови у просторі зображень матимуть вигляд

(7.4)

де .

Таким чином, вважаючи, що є оригіналом, операційний метод приводить розв’язання поставленої неста-ціонарної задачі (7.2)–(7.3) до розв’язання звичайного дифе-ренціального рівняння другого порядку

(7.5)

з крайовими умовами (7.4), де , , , – ком-плексний параметр.

Приклад 7.1 Кінці струни і закріплені жорстко. Початкове відхилення задано рівністю , початкова швидкість рівна нулю. Знайти відхилення при .

• Задача зводиться до розв’язання диференційного рівняння

,

яке задовольняє задані додаткові умови

П.У. К.У.

Застосуємо перетворення Лапласа до функції за змінною . Позначивши зображення шуканої функції через , запишемо наступні співвідношення:

, , ,

,

.

Тоді на основі цих співвідношень та сформульованої зада-чі з додатковими умовами, одержимо у просторі зображень наступну задачу

, (7.6)

К.У.

Розв’язок лінійного неоднорідного диференціального рівняння другого порядку шукаємо у вигляді:

,

де – загальний розв’язок відповідного однорідного рівняння .

Характеристичне рівняння . Звідси

.

Тоді загальний розв’язок однорідного рівняння буде

.

Частинний розв’язок неоднорідного рівняння знайдемо у вигляді .

Для знаходження невідомої сталої підставимо частин-ний розв’язок у (7.6) та отримаємо рівняння

.

Звідси

.

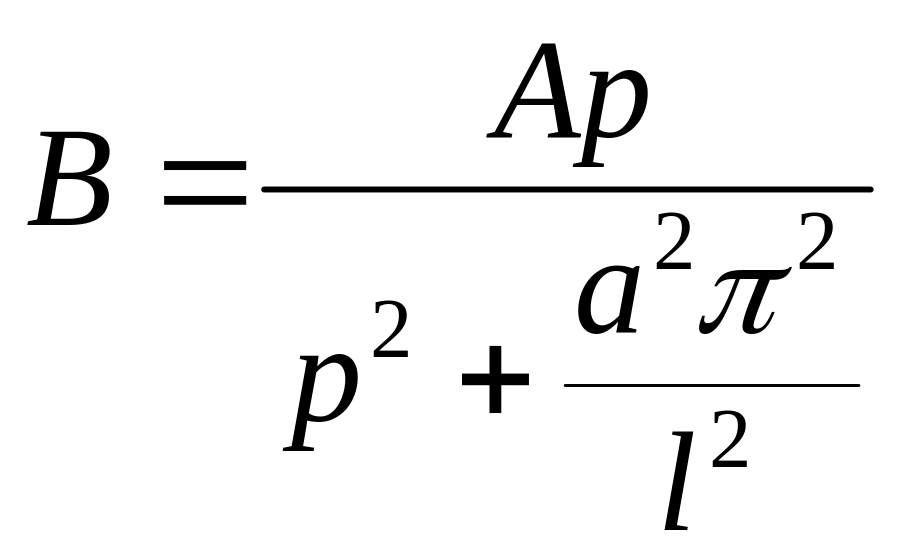Тоді

Загальний розв’язок рівняння буде мати вигляд:

.

Підставляючи розв’язок у крайові умови, знайдемо невідомі константи

Отже, оригіналом для з врахуванням формули оберненого перетворення

буде функція

,

яка є розв’язком поставленої задачі.

Приклад 7.2 Знайти розв’язок рівняння теплопровідності , який задовольняє початковим і граничним умовам ( ), .

Задача зводиться до розв’язання диференційного рівняння

, яке задовольняє задані додаткові умови

П.У. , К.У.

Застосуємо перетворення Лапласа до функції за змінною . Позначивши зображення шуканої функції через , запишемо наступні співвідношення:

, , ,

.

Вихідне рівняння після підстановки отриманих формул та крайові умови у просторі зображень набудуть вигляду

,

К.У.

Розв’язок отриманого лінійного неоднорідного диференціального рівняння другого порядку шукатимемо у вигляді:

,

де – загальний розв’язок відповідного однорідного рівняння:

,

характеристичне рівняння:

.

Звідси

.

Тоді загальний розв’язок однорідного рівняння буде

.

Частинний розв’язок неоднорідного рівняння знайдемо у вигляді

.

Для знаходження невідомої сталої підставимо частин-ний розв’язок у (7.6) та отримаємо рівняння

.

Звідси

.

Тоді,

.

Загальний розв’язок рівняння буде мати вигляд:

.

Підставляючи розв’язок у крайові умови, знайдемо невідомі константи

Отже, оригіналом для з врахуванням формули оберненого перетворення

буде функція

,

яка і буде розв’язком поставленої задачі.