4. Очевидно, что для плотности распределения спораведливо соотношение:

Функция распределения F(x) может быть задана как единая или составная функция, а так же может задаваться графически. Для непрерывной случайной величины график функции распределения всегда непрерывная линия, тогда как график плотности распределения может иметь одну или несколько точек разрыва первого рода.

Пример. Функция распределения непрерывной случайной величины Х задана выражением:

Найти плотность распределения. Построить график плотности распределения и вычислить вероятность попадания случайной точки в промежуток .

Решение.

График функции распределения задан составной функцией. Её вид приведен на рис. 6. Плотность распределения получаем дифференцированием функции распределения для каждого из указаных в условии задачи промежутков временни. Аналитическое выражение плотности распределения имеет вид:

Графики функции распределения F(X) и плотности распределения F(x) приведены ниже (см. рис. 6). Геометрически график функции распределения выражает закон нарастания площади под графиком плотности распределения при увеличении текущего значения аргумента х. в пределе, при , эта площадь всегда становится равной 1. в данном примере график плотности распределения имеет одну точку разрыва первого рода при х = 3. Заштрихованная на нём площадь численно равна вероятности попадания случайной точки на указанный промежуток.

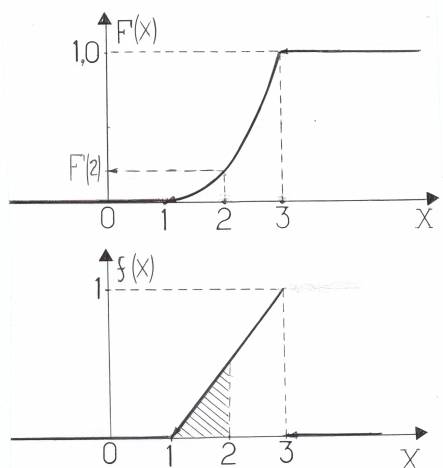
Рис. 6.

Вероятность попадания случайной точки на участок можно подсчитать двумя способами:

Лекция №5.

Числовые характеристики случайной величины.

Решение многих практических задач не требует знания исчерпывающих характеристик случайной величины, каковыми являются законы распределения, а достаточно знания их основных числовых характеристик. Таких характеристик две. Первая характеристика указывает положение случайной величины на числовой оси и называется «математическим ожиданием». Её механическим аналогом для дискретной случайной величины служит центр тяжести системы из конечного числа материальных точек известных масс, распределённых определённым образом на числовой оси. При этом суммарная масса всех точек должна быть равна единице.

Пусть дискретная случайная величина задана своим рядом распределения:

Х	Х1	Х2	…….	хn
Р(х)	Р1	Р2	…….	Рn

Тогда математическое ожидание определится формулой:

Если с. в. принимает бесконечное, но счётное число значений, то формула примет вид:

Определение. Математическим ожиданием дискретной случайной величины наз. сумма парных произведений всех возможных значений случайной величины на вероятности этих значений.

Механическим аналогом математического ожидания для непрерывной случайной величины служит центр тяжести тонкого прямого стержня конечной длины, размещённого определённым образом на числовой оси, закон изменения линейной плотности которого известен и масса которого равна единице.

Пусть непрерывная с.в. принимает свои значения из промежутка числовой оси, плотность распределения которой на этом промежутке задана функцией f(x). Тогда её математическое ожидание выразится формулой:

Отметим свойства математического ожидания с. в. Х.

1. М(С)=С, если С – константа;

2. M(CX)=CM(X);

3. M(X 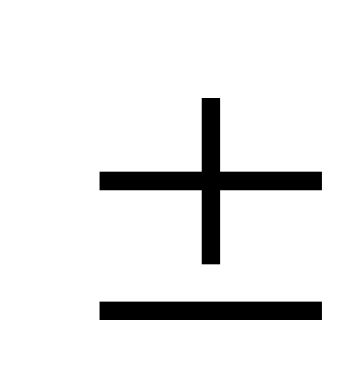Y)=M(X) M(Y), Х и У – случайные величины;

4. M(XY)=M(X)M(Y);

5. M(aX+b)=aM(X)+b, здесь: а и в – константы;

6. М(Х-М(Х)) = 0.

Пример. Производится 5 выстрелов из орудия. Вероятность попадания при каждом выстреле равна р=0,6. Найти математическое ожидание числа попаданий (среднее число попаданий).

Решение.

Возможные значения с. в. Х: 0; 1; 2; 3; 4; 5 –попаданий при пяти выстрелах. Условия задачи соответствуют требованиям, при которых справедлива формула Бернулли. Если вероятность попадания при каждом выстреле равна р = 0,6, то вероятность противоположного события – промаха, равна q = 0,4. Посчитаем вероятности возможных значений:

И т. д. Ряд распределения случайной величины Х будет иметь вид:

xi	0	1	2	3	4	5
pi	0,01024	0,0768	0,2304	0,3456	0,2592	0,0777

Математическое ожидание:

Пример. непрерывная с. в. Х задана плотностью распределения:

Найти математическое ожидание М(Х).

Решение.

В формуле, задающей плотность распределения, содержится неизвестный параметр а. Для его определения используем свойство 4 плотности распределения.

Размерность математического ожидания совпадает с размерностью случайной величины.

Второй числовой характеристикой случайной величины является характеристика, показывающая, как сильно её возможные значения разбрасываются вокруг математического ожидания (среднего значения).

Механическим аналогом характеристики рассеивания для дискретной случайной величины является момент инерции материальных точек, размещённых определённым образом на числовой оси, относително своего центра тяжести, при этом суммарная масса точек равна единице.

В теории вероятности эта характеристика получила название «дисперсия» D(X).

Пусть дискретная с. в. задана своим рядом распределения (см. табл. выше). Тогда её дисперсия (по аналогии с моментом инерции) будет иметь вид:

Механическим аналогом дисперсии для непрерывной случайной величины служит момент инерции тонкого прямого стержня, размещённого определённым образом на числовой оси, относительно его центра тяжести, причём масса стержня равна единице и известен закон распределения его линейной плонности.

Пусть возможные значения непрерывной случайной величины заполняют промежуток числовой оси , а его плотность распределения задана функцией f(x). Тогда её дисперсия будет иметь вид:

При вычислении дисперсии удобно пользоваться другими формулами, которые получим из вышеприведенных:

Определение. Дисперсия равна математическому ожиданию квадрата случайной величины без квадрата её математического ожидания.

Если возможных значений дискретной случайной величины - бесконечное, но счётное множество, или если непрерывная случайная величина принимает свои значения на всей числовой оси, то формулы для дисперсии принимают вид:

Свойства дисперсии.

1. D(C) =0, если С- константа;

2. D(CX)=C²D(X);

3. D(X+Y)=D(X)+D(Y), здесь Х и У – случайные величины;

4. D(aX+b)=a²D(X), здесь а и в - константы.

Размерность дисперсии равна квадрату размерности самой слчайной величины.

Наряду с дисперсией широкое применение находит ещё одна характеристика рассеивания, называемая средним квадратическим отклонением (с.к.о.), которое обозначается символом . Вычисляется с.к.о. через дисперсию по формуле: Размерность с.к.о. совподает с размерностью самой случайной величины.

Свойства с.к.о.

1. если с – константа;

2.

3. если Z = Х У, где Х и У – случайные величины;

4. , здесь а и в – константы.

Вспомогательные числовые характеристики случайных величин.

К вспомагательным характеристикам с.в. относятся мода и медиана.

Определение. Модой М₀ дискретной с. в. называется её наиболее вероятное значение.

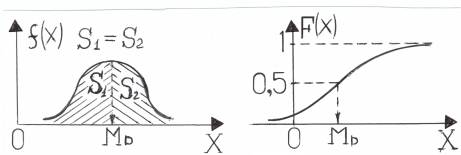
Определение. Модой М₀ непрерывной с. в. называетсятакое её значение, при котором плотность распределения f(х) имеет максимум.

На приведенных ниже рисунках показаны случаи одномодального распределения, хотя возможны и двухмодальные распределения.

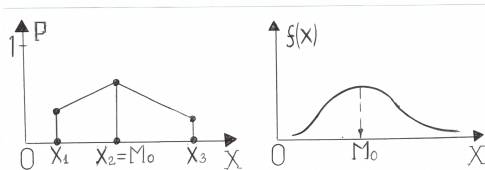
Определение. Медианой М_D непрерывной с. в. Х называется такое её значение, относительно которого равновероятно получение большего или меньшего значения: Р(Х<M_D)=P(X>M_D).

Геометрически – это точка оси ОХ, ордината в которой делит площадь под кривой распределения плотности f(x) пополам, или точка оси ОХ, в которой функция распределения F(x) = 0,5.

Медианой как числовой характеристикой случайной величины обычно пользуются применительно к непрерывным случайным величинам, хотя формально её можно определить и по отношению к дискретным случайным величинам.

Арифметические операции над случайными величинами.

Пусть две дискретные случайные величины Х и У заданы своим рядом распределения.

Х	х1	х2	х3
р	р1	р2	р3	1

У	у1	у2
s	s1	s2	1

Закон распределения суммы Х + У двух случайных величин имеет вид:

							1

Закон распределения произведения ХУ двух случайных величин имеет вид:

		s2					1

Примеры.

1. Случайная величина Х задана своим рядом распределения. Построить функцию и многоугольник рсспределения, найти числовые характеристики распределения – математическое ожидание, дисперсию, среднее квадратическое отклонение и наиболее вероятное значение – моду.

xi	-5	2	3	4
pi	0,3	0,4	0,2	0,1

Решение.

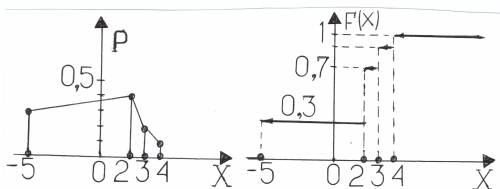
Многоугольник распределения и функция распределения F(х) приведены

на рисунках, расположенных ниже. Наиболее вероятное значение заданной случайной величины М₀ = 2.

Математическое ожидание: М(Х) = ед. с.в.

Дисперсия: D(X) = ед² с.в.

Среднее квадратическое отклонение: ед. с.в.

Мода распределения равна: M_D =2 ед. с.в.

2. Случайная величина Х задана плотностью распределения f(x).

Найти функцию распределения F(x), построить графики функции распределения и плотности распределения, определить числовые характеристики случайной величины.

Решение.

Функцию распределения находим по формуле:

Графики функции распределения и плотности распределения приведены ниже.

Математическое ожидание: ед. с. в.

Дмсперсия: ед² с. в.

С.к.о.: ед. с. в.

Для нахождения моды найдём экстремум графика плотности:

M₀= 4 ед. с. в.

Медиану найдём, используя плотность распределения:

ед. с. в.