Математическая статистика.

Лекция №8.

Введение.

Наука, занимающаяся разработкой методов получения, описания и обработки опытных данных с целью изучения закономерностей случайных массовых явлений, называется математической статистикой.

При помощи мат. статистики осуществляется рациональная обработка результатов испытаний теоретико – вероятностными методами. Все задачи мат. статистики касаются вопросов обработки наблюдений над массовыми случайными явлениями. Наиболее важными по своим практическим применениям являются следующие задачи:

а) Оценка на основании результатов измерений неизвестной функции распределения F*(x);

б) Оценка на основании результатов измерений неизвестных числовых характеристик распределения;

в) Статистическая проверка гипотез, заключающаяся в проверке предположения о наличии того или иного вида закона распределения.

В настоящем курсе лекций не ставится задача строгого изложения математической статистики, поэтому некоторые вопросы теории изложены кратко, без сложных доказательств. Назначение приведенного материала состоит в изложении практических методов обработки статистических данных при большом и малом объёмах выборки.

Обработка статистических данных при большом

объёме выборки ( n > 30 ).

Изложение методов обработки статистияческих данных при большом объёме выборки осуществим на примере обработки данных хронометрических карт затраты времени студентами при выполнении ими контрольной работы по высшей математике.

Введём в обращение некоторые понятия, используемые в математической статистике.

Генеральной совокупностью называют случайную величину Т, функция распределения F(t) которой неизвестна.

Выборкой объёма n из генеральной совокупности Т называют n реализаций случайной величины Т в n независимых испытаниях.

Ниже приводится выборка объёма n =79 – результаты оценки времени в минутах, затраченного 79 студентами при выполнении ими контрольной работы по математическому анализу. Таблица 1.

10. 58 25 16 18 16 14 16 19 13 24 10 26 11 17 17 14 34 28 18 7 25

13. 8 17 23 13 14 16 19 22 16 25 12 13 28 23 16 18 40 26 21 24 43

17. 20 15 17 19 53 6 32 45 40 15 18 23 16 19 12 22 26 14 43 15 28

20 15 34 21 21 24 32 15 11 18 8 20 22 n = 79.

Если приведенные варианты расположить в убывающем или возрастающем

порядке, то они образуют вариационный ряд. Если при этом осуществляется группировка повторяющихся вариант, то такая таблица образует дискретный вариационный ряд. Для его построения в первой колонке, обычно в порядке возрастания, выписываются сверху вниз все несовпадающие значения вариант. Во второй колонке ставятся пометки в виде чёрточек, каждая из которых соответствует числу повторений варианты. В третью колонку записывают результат подсчёта чёрточек (разрядные частоты). Дискретный вариационный ряд, построенный по выборке объёмом n = 79 (см. таблица 1), приведен ниже (таблица 2).

Таблица 2.

ti мин.	Пометки	ni	ti мин.	Пометки	ni
6	/	1	21	///	3
7	/	1	22	///	3
8	//	2	23	///	3
10	//	2	24	///	3
11	//	2	25	///	3
12	//	2	26	///	3
13	////	4	28	///	3
14	////	4	32	//	2
15	/////	5	34	//	2
16	///// //	7	40	//	2
17	/////	5	43	//	2
18	/////	5	45	/	1
19	////	4	53	/	1
20	///	3	58	/	1

Полученная сводка данных ещё не является удобной для последующих исследований. Поэтому, если объём выборки велик (как в нашем случае), необходимо составить интервальный вариационный ряд. Для этого всю выборку распределяют по непересекающимся интервалам, совокупность которых перекрывает весь диапазон значений полученных t_i.

Чтобы характерные особенности распределения не были завуалированны, а нехарактерные были бы сглажены, желательно иметь число интервалов нечётным, а в каждом частичном интервале содержалось бы не менее 8 – 10 вариант.

На практике для определения числа интервалов часто используют формулу:

интервала. Для определения ширины интервалов на практике поступают так: разность между наибольшим и наименьшим значениями вариант (см. таблицу 1 – выделено жирным шрифтом) делят на принятое число интервалов.

Если принять число интервалов, равным 9, то минут. Округление до целых единиц необходимо всегда производить в сторону увеличения, ибо в противном случае крайние значения вариант не попадут в общую ширину интервала. При таком округлении весь интервал несколько расширяется, причём расширение можно производить как в сторону меньших, так и в сторону больших значений вариант. Такое расширение всего интервала не отражается на значениях параметров распределения. Итак, количество частичных интервалов к=9, а ширина каждого интервала минут.

Условимся расширение всего интервала вариант производить в сторону больших значений вариант. Чтобы ни одно из имеющихся значений вариант не попало на границу интервала, сдвинем границы интервала на 0,5 минуты. Составляем интервальный вариационный ряд (см. таблицу 3) и одновременно для последующих вычислений запишем серидины интервалов с указанием частот попавших в интервал наблюдений и относительных частот.

Таблица 3.

№ п.п.	Интерв. ряд	Середины инт.	Частоты	Относит. част.
1	5,5 – 11,5	8,5	8	8/79 = 0,1012
2	11,5 – 17,5	14,5	27	27/79 = 0,3418
3	17,5 – 23,5	20,5	21	21/79 = 0,2658
4	23,5 – 29,5	26,5	12	12/79 = 0,1519
5	29,5 -35,5	32,5	4	4/79 = 0,0506
6	35,5 – 41,5	38,5	2	2/79 = 0,0253
7	41.5 – 47,5	44,5	3	3/79 = 0,0379
8	47,5 – 53,5	50,5	1	1/79 = 0,0127
9	53,5 - 59,5	56,5	1	1/79 = 0,0127

Точечные оценки числовых характеристик распределения.

Числовые характеристики распределения можно вычислить по формулам, аналогичным формулам теории вероятности:

а) среднее выборочное время (аналог математического ожидания).

, где N = – объём выборки (число наблюдений) (см. таблица 2); n_i – частоты; t_i – варианта.

б) выборочная дисперсия

в) стандарт (аналог с. к. о.)

Однако, вычисления среднего выборочного и выборочной дисперсии по приведенным формулам представляет собой весьма трудоёмкую задачу. Поэтому на практике при вычислении упомянутых параметров целесообразно использовать условные варианты. С этой целью используют интервальный вариационный ряд (см. таблица 3), принимая середины интервалов в качестве представителей значений вариант данного интервала. Тогда суммирование в вышеприведенных формулах надо проводить не от 1 до N, а от 1 до к, где к – количество интервалов.

Итак:

а) среднее выборочное время: где

Здесь: С – ложный нуль (берётся варианта с наибольшей частотой повторения);

n – объём вфыборки;

h – ширина интервалов;

где t_i – cередины интервалов;

б) выборочная дисперсия: где

Для вычисления точечных оценок числовых характеристик составляем таблицу 4.

Таблица 4.

№ Интер.	Интервал	Середина инт. ti	Частота ni
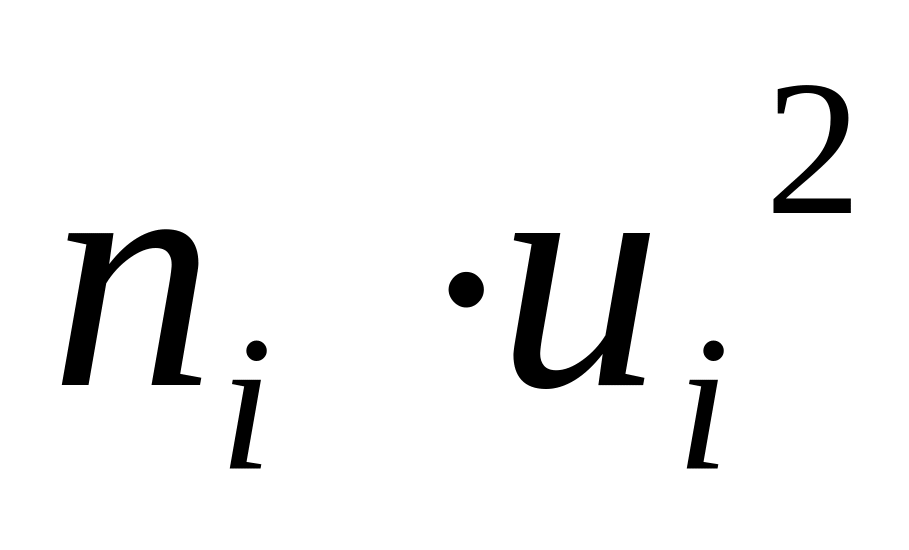
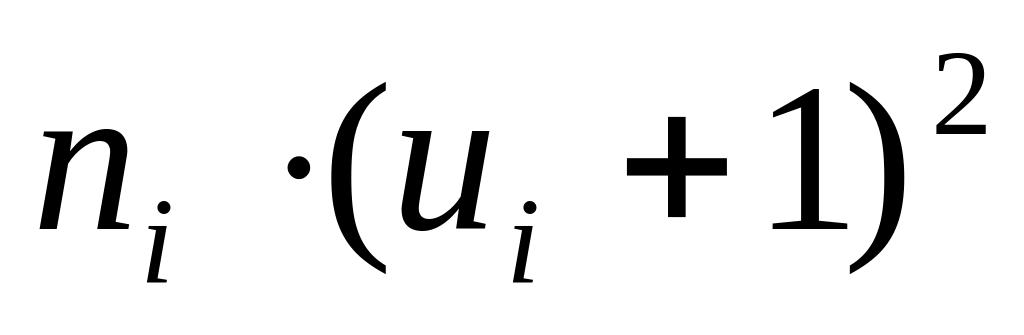
1	5,5 – 11,5	8,5	8	- 1	- 8	8	0
2	11,5-17,5	14,5	27	0	0	0	27
3	17,5-23,5	20,5	21	1	21	21	84
4	23,5-29,5	26,5	12	2	24	48	108
5	29,5-35,5	32,5	4	3	12	36	64
6	35,5-41,5	38,5	2	4	8	32	50
7	41,5-47.5	44,5	3	5	15	75	108
8	47,5-53,5	50,5	1	6	6	36	49
9	53,5-59,5	56,5	1	7	7	49	64
			=79		85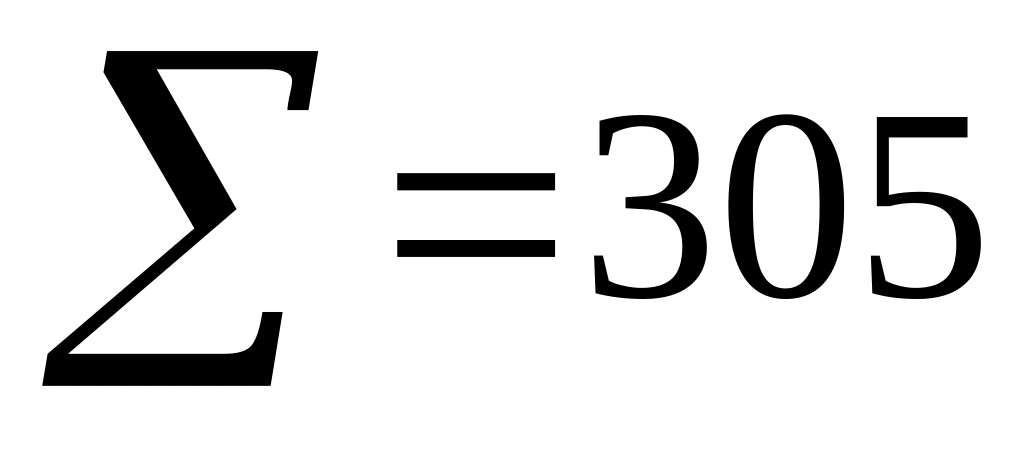

Так как варианта t₂ = 14,5 мин. имеет наибольшую частоту n₂ = 27, то её мы и принимаем за ложный нуль, т. е. С = 14,5. Протяжённость всех временных интервалов одинакова и равна h = 6 минут. Последняя колонка таблицы 4 необходима для контроля правильности вычислений:

Проверка. , расчёт выполнен правильно.

Последовательно определяем:

Построение статистических законов распределения по данным выборки.

Статистической функцией распределения случайной величины Х называется закон изменения относительной частоты события Х < х, построенный по статистическому дискретному ряду выборки: , или, в обозначениях рассматриваемого примера, это выглядит так:

Для построения статистической функции распределения используем таблицу 5.

Таблица 5.

Середина интервала ti	Частота ni	Относит. частота		Кумул. распр.
t1 = 8,5	n1 = 8	r1 = 0,1012		0,0506
14,5	27	0,3418	0,1012	0,2721
20,5	21	0,2658	0,4430	0,5759
26,5	12	0,1519	0,7088	0,78475
32,5	4	0,0506	0,8607	0,886
38,5	2	0,0253	0,9113	0,92395
44,5	3	0,0379	0,9366	0,95555
50,5	1	0,0127	0,9745	0,9808
56,5	1	0,0127	0,9872	0,9935
			0,9999

На странице 60 приведен график статистической функции распределения , построенный с использованием первой и четвёртой колонки таблицы 5 (ступенчатая линия). Кумулятивный график построен с использованием первой и пятой колонки таблицы 5 (непрерывная кривая, проходящая через средние точки «ступеней»). Этот график даёт представление о неизвестной функции распределения случайной величины Т. Для дальнейшего анализа выборки сравним данные расчёта с выводами по нормальному закону. Используя кумулятивный график, вычислим относительные частоты попадания случайной точки в интервалы, определяемые правилом одного, двух и трёх «сигм», и сравним полученные числа с вероятностями попадания нормально распределённой случайной величины в те же интервалы. Такой методикой можно пользоваться при выдвижении предварительной гипотезы о наличии в исследуемой выборке нормального закона распределения вероятности. При этом следует иметь ввиду, что кумулятивный график должен быть построен достаточно точно, с использованием, например, миллиметровой бумаги для получения достоверной информации.

а) По правилу одного «сигма» для выборки имеем:

По правилу одного «сигма» для нормального закона должно быть 0,68.

б) По правилу «двух сигм» числа соответственно равны:

должно быть 0.95.

в) По правилу «трёх сигм» получаем:

должно быть 0,997.

Сравнение цифр показывает, что максимальное расхождение не превышает 5%, что позволяет выдвинуть гипотезу о наличии в нашей выборке закона распределения, близкого к нормальному (в дальнейшем эту гипотезу проверим, используя критерии согласия).