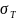7. Розкрити сутність моделювання напруження течії металу  на основі методу термомеханічних коефіцієнтів. Принципи побудови графічних залеж-ностей для термомеханічних коефіцієнтів

σ прямо пропорционально зависит от степени и скорости деформации (т.к. чем они выше тем более выражено наблюдается явление упрочнения) и обратно пропорционально температуре деформации (т.к. чем больше температура тем меньше усилия необходимо приложить для начала пластической деформации).

Профессор Зюзин предложил следующую зависимость для определения напряжения течения металла

, где 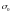-базисное значение напряжения течения металла, при =0.1, = 10с^-1, T= 1000 С

-термомеханические коэффициенты

Термомеханический коэффициент Зависимость для аппроксимации точек

k_ε=σ_ε/σ₀ K_ε=A₁εⁿ¹

k_u=σ_u/σ₀ K_u=A₂uⁿ²

k_Т=σ_Т/σ₀ K_Т=A₃e^(-n3*T)

σ_ε - значение напряжения течения металла при заданном текущем и фиксированных базових значениях U и T

σ_u - значение напряжения течения металла при заданном текущем U и фиксированных базових значениях и T

σ_T - значение напряжения течения металла при заданном текущем T и фиксированных базових значениях и U

Темомеханические коэффициенты находятся на основе имеющейся пластометрической экспериментальной информации.

Алгоритм нахождения k_ε

Назначается диапазон изменения min< < max по имеющейся экспериментальной информации. Изменяя находят k_ε=σ_ε/σ₀ при

фиксированных базовых значениях U и T.

Далее, при помощи метода наименьших квадратов находятся константы A₁,n₁

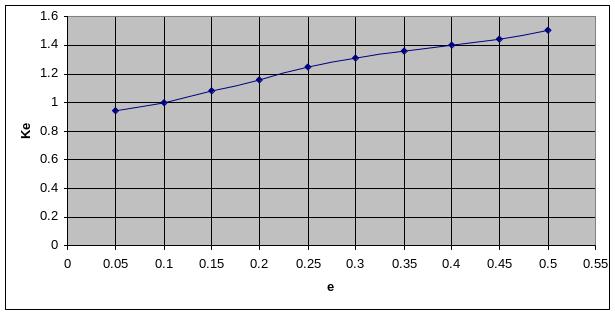
8. Раскрыть сущность метода получения формулы . Раскрыть сущность метода расчета констант в данной формуле.

Профессор В.И. Зюзин предложил следующую зависимость:

,

где σ₀ - базисное значение напряжения течения металла, установленное при степени деформации ε=0,1, скорости деформации и=10 с^-1 и температуре Т=1000 ⁰С;

- термомеханические коэффициенты.

Для нахождения термомеханических коэффициентов были построены графики.

При и=10 с^-1 и Т=1000 ⁰С

k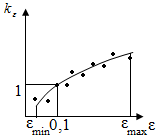 _ε в точках определены по формуле _{на основе экспериментальной информации. Эти точки аппроксимируются уравнением: .}

Коэффициенты А₂, т₂ находим по методу наименьших квадратов. Согласно методу, наилучшими параметрами будут те, для которых сумма квадратов отклонений будет минимальна.

График k_u строится аналогично при ε=0,1 и Т=1000 ⁰С.

При ε=0,1 и и=10 с^-1

k _T в точках определены по формуле

Точки аппроксимируются по формуле

, где

9. Раскрыть сущность моделирования течения металла на основе метода планируемого эксперимента.

Напряжение течения металла зависит от марки стали, скорости и степени деформации. Это значит, что у нас 3 фактора : Известны также пределы изменения этих факторов. Планирование на основе многофакторного эксперимента позволяет уменьшить число опытов и повысить точность коэффициентов получаемых уравнений регрессии. Для трехфакторного эксперимента число опытов равно 15, а звездное плечо равно 1,215.

Для начала необходимо определить кодовые значения факторов и соответствующие им натуральные значения. Например:

Где б- шаг варьирования.

Связь между натуральными значениями и кодовыми определяют по формуле:

где Х_і – натуральное значение фактора;

Х_і0 – натуральное значение фактора на среднем уровне;

х_і – кодовое значение фактора.

После проведения всех 15 опытов, получим план-матрицу эксперимента:

	X1	X2	X3	ε	U (1/с)	T (0С)	σэксп (МПа)
1	-1	-1	-1
2	+1	-1	-1
∙ ∙ ∙
15	0	0	0

При помощи программы Statistica, которая основана на методе наименьших квадратов (т.е. сумма квадратов отклонений расчётных точек от исходных точек должна быть минимальной), получим коэффициенты, входящие в уравнение расчёта напряжения течения металла по формуле профессора В.И Зюзина: А_, п₁, п₂, п_3. Подставим их в уравнение и получим окончательную формулу для расчета