20.Плоской фигурой q называется часть плоскости, ограниченная простой замкнутой кривой l. При этом кривую l будем называть границей фигуры q.

Пусть - числовое множество площадей вписанных в плоскую фигуру Q многоугольников, а - множество площадей описанных вокруг фигуры Q многоугольников. Очевидно, эти множ-ва ограничены: - сверху (площадью описанного вокруг фигуры Q многоугольника), - снизу (напр. нулем). Обозначим , . Эти числа называются соответственно нижней и верхней площадью фигуры Q.

Плоская фигура Q называется квадратируемой, если верхняя площадь этой фигуры совпадает с ее нижней площадью . При этом число называется площадью фигуры Q.

Теорема. Для того чтобы плоская фигура Q была квадратируемой, необходимо и достаточно, чтобы для любого положительного числа ε можно было указать такой описанный вокруг фигуры Q многоугольник и такой вписанный в фигуру многоугольник, что <ε.

Плоская фигура в ПДСК представляет собой квадратируемую фигуру, площадь P которой может быть вычислена по формуле .

y Рисунок к билету №23 часть1.

a b

0 x0 x1 x2 xn-1 xn x

Док-во. Т.к. непрерывная на функция интегрируема, то для любого ε>0 можно указать такое разбиение Р отрезка , что разность S-s<ε, где S и s – соотв. верхняя и нижняя границы разбиения. Но S и s равны соответственно и - площади многоугольников, первая из которых содержит пл. фигуру, а вторая содержится в ней. Т.к. <ε, то в силу теоремы (выше) пл. фигура квадратируема. Поскольку предел при (в суммах Дарбу) верхних и нижних сумм равен и , то площадь Р пл. фигуры может быть найдена по данной формуле.

Пусть кривая L задана в полярной системе координат уравнением , , причем функция непрерывна и неотрицательна на отрезке . Плоскую фигуру. Ограниченную лучами, составляющими с полярной осью углы α и β, мы будем называть криволинейным сектором.

Криволинейный сектор представляет собой квадратируемую фигуру, площадь Р которой может быть вычислена по формуле .

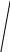
Рисунок к билету №23 часть2.

L

Α β

Док-во. Рассм. Разбиение Т отрезка точками и для каждого отрезка разбиения построим круговые секторы, радиусы которых равны минимальному и максимальному значениям функции на отрезке. В результате получим две веерообразные фигуры, первая из которых содержится в секторе, а вторая содержит сектор. Площади и этих фигур равны соответственно и . Первая из этих сумм является нижней суммой s для , а вторая – верхней. Т.к. ф-я интегрируема, то разность может быть сколь угодно малой (т.е. меньше ε). Т.к. справедливы неравенства , то, очевидно, <ε. Отсюда вытекает квадратируемость сектора, а из неравенств – справедливость формулы.

Пусть линия задана параметрически. заданы две непрерывные функции, кусочно-гладкие, т.е. имеющие непрерывные производные.

Рассмотрим их на интервале . Если отображение взаимно однозначное, то кривая простая.

Если , то кривая замкнутая.

Найдем площадь простой замкнутой кривой.

Y t3 Рисунок к билету №23 часть 3.

d

t 0=T t2

c

a t1 b x

Площадь плоской фигуры, ограниченной двумя кривыми в ПДСК вычисляется по формуле (по свойству интегрируемых функций). В нашем случае формула выглядит:

Если рассматривать ось ОУ, получим