51. Правила диференціювання сталої, суми, добутку, частки функцій та наслідки з них

Основні правила диференціювання

Теорема 1. Похідна сталої дорівнює нулю, тобто якщо у = с, де с = const, то .

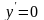Теорема 2. Похідна алгебраїчної суми скінченної кількості диференційовних функцій дорівнює алгебраїчній сумі похідних цих функцій: .

Теорема 3. Похідна добутку двох диференційовних функцій дорівнює добутку першого множника на похідну другого плюс добуток другого множника на похідну першого:

.

Теорема 4. Сталий множник можна виносити за знак похідної:

, де .

Теорема 5. Якщо чисельник і знаменник дробу диференційовні функції (знаменник не перетворюється в нуль), то похідна дробу також дорівнює дробу, чисельник якого є різницею добутків знаменника на похідну чисельника і чисельника на похідну знаменника, а знаменник є квадратом знаменника початкового дробу .

Зауваження. Похідну від функції , де , зручно обчислювати як похідну від добутку сталої величини на функцію u (x):

.

52.Похідна сталої та функції у=х. Таблиця похідних.

1) Похідна постійної величини C дорівнює нулю,тобто C0

2) Якщо кожна з функцій u(x) та v(x) диференційована в точці x , то добуток цих функцій також має похідну в точці x , причому цю похідну знаходять за формулою

u(x)v(x)u(x)v(x)u(x)v(x)

3) Якщо u(x) та v(x) мають похідні в точці x і v(x)0, то частка цих функцій також має похідну в точці x , яку знаходять за формулою

4)Якщо кожна із функцій f1 (x), f 2 (x),...,f n (x)

(n – скінченне число) диференційована в деякі точці x , то їх алгебраїчна сума також є диференційованою в цій точці, причому похідна алгебраїчної суми цих функцій дорівнює такій самій алгебраїчній сумі їх похідних.

53. Геометричний зміст похідної. Рівняння дотичної. Поняття нормалі до графіка функції та її рівняння. Економічний зміст похідної

4.1.2. Геометричний зміст похідної

Означення. Дотичною до кривої L у точці М називається граничне положення МN січної ММ₁ при прямуванні точки М₁ по кривій L до точки М (рис. 4.1).

Нехай крива, задана рівнянням , має дотичну в точці М (х, у). Позначимо (рис. 4.2) кутовий коефіцієнт дотичної МN: . Надамо в точці х приросту , тоді ордината у набуде приросту .

З 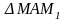випливає, що . Коли , то 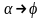і січна прямує до положення дотичної МN.

Таким чином, .

Рис. 4.1 Рис. 4.2

Оскільки , то тобто похідна чисельно дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою х. У цьому полягає геометричний зміст похідної.

Нехай рівняння прямої, що проходить через задану точку М₀ (х₀; у₀) у даному напрямі (рис. 4.4):

, Оскільки , то з виразу (4.2) ді- станемо рівняння дотичної у вигляді

.

Нормаллю до графіка функції в точці М₀ називається перпендикуляр, проведений до дотичної в цій точці:

Для пояснення економічного змісту похідної розглянемо задачу про продуктивність праці. Нехай функція відображає кількість виробленої продукції u за час t і необхідно знайти продуктивність праці в момент t₀.

За період часу від t₀ до кількість виробленої продукції зміниться від значення 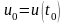до значення 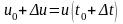; тоді середня продуктивність праці за цей період часу . Очевидно, що продуктивність праці в момент t₀ можна визначити як граничне значення середньої продуктивності за період часу від t₀ до при , тобто

.

Таким чином, продуктивність праці є похідна від обсягу вироб­леної продукції по часу.

Застосування диференціального числення для дослідження економічних об’єктів та процесів на основі аналізу цих граничних величин дістало назву граничного аналізу. Граничні величини характеризують не стан (як сумарна чи середня величини), а процес зміни економічного об’єкта. Таким чином, похідна виступає як швидкість зміни деякого економічного об’єкта (процесу) за часом або відносно іншого об’єкта дослідження. Але необхідно врахувати, що економіка не завжди має змогу використовувати граничні величини у зв’язку з неподільністю багатьох об’єктів економічних розрахунків та перервністю (дискретністю) економічних показників у часі (наприклад, річних, квартальних, мі- сячних та ін.). Водночас у деяких випадках можна знехтувати дискретністю показників і ефективно використовувати граничні величини.