
- •2.4. Основное уравнение молекулярно-кинетической теории газов
- •2.5. Постоянная Больцмана
- •3.1. Длина свободного пробега молекул
- •3.2. Скорость газовых молекул
- •3.3. Распределение Максвелла
- •4.1. Предмет термодинамики. Постулаты термодинамики
- •4.2. Температурные шкалы. Абсолютная температура
- •4.3. Температура в молекулярно-кинетической теории
- •4.4. Внутренняя энергия. Работа. Теплота
- •4.5. Первое начало термодинамики.Понятие теплоемкости
- •4.6. Применение первого начала термодинамики к описанию изопроцессов в идеальном газе
- •4.7. Первое начало термодинамики как принцип эквивалентности теплоты и работы
- •Экспериментальная установка Джоуля
- •4.8. Невозможность вечного двигателя первого рода
- •4.9. Принципы работы тепловых машин
- •4.10. Цикл карно. Кпд тепловых двигателей
- •Циклы тепловых двигателей
- •4.11. Обратимые и необратимые процессы
- •4.12. Второй закон термодинамики
- •4.13. Теорема карно
- •4.14. Энтропия. Неравенство клаузиуса. Математическое выражение второго начала термодинамики
- •4.14. Энтропия. Неравенство клаузиуса. Математическое выражение второго начала термодинамики
- •4.15. Статистический смысл второго начала термодинамики
- •4.16. Энтропия и термодинамическая вероятность. Формула больцмана
- •4.16. Энтропия и термодинамическая вероятность. Формула больцмана
- •4.17. Энтропия и беспорядок
2.4. Основное уравнение молекулярно-кинетической теории газов
Идеальный газ можно рассматривать как собрание свободно двигающихся молекул, между которыми отсутствуют силы взаимного притяжения. Сами молекулы при соударениях между собой и со стенками сосуда ведут себя как абсолютно упругие шарики конечных, но весьма малых размеров.
Реальные газы при не очень низких температурах и не сверхвысоких давлениях близки по своим свойствам и идеальному газу. Давление газа определяется ударами молекул о стенки сосуда. Попробуем вычислить его.
|
При ударе о стенку молекула упруго отскакивает, и ее импульс mv изменяется на величину
|
|
Это изменение импульса определит импульс силы, действующий на молекулу со стороны стенки. Обозначим через ΔF силу удара и через δt – время удара. Очевидно, что
|
|
По III закону Ньютона сила, численно равная ΔF, будет действовать на стенку. Молекула, отскочив от стенки, долетит до противоположной, отскочит от нее и вернется к первой стенке через время
|
|
Средняя сила
![]() ,
действующая на стенку за время между
двумя последовательными ударами,
найдется из условия, что ее импульс
,
действующая на стенку за время между
двумя последовательными ударами,
найдется из условия, что ее импульс
![]() должен
быть численно равен импульсу, действующему
во время удара, т.е.
должен
быть численно равен импульсу, действующему
во время удара, т.е.
|
|
Учитывая это, можно записать:
|
|
Это среднее
значение силы ударов одной молекулы.
Но число молекул, движущихся между
противоположными стенками, n', и
каждая имеет свою скорость. Учтя это,
запишем для средней силы
![]() ,
действующей на стенку:
,
действующей на стенку:
|
|
Умножим и поделим полученное выражение на n'. Тогда
|
|
Обозначая
|
|
назовем полученную величину средней квадратичной скоростью. Учитывая, что , запишем:
|
|
Поделим левую
и правую части на l2, тогда
слева будет давление
![]() :
:
|
|
Дробь
![]() определяет
число молекул в единице объема, т.е.
концентрацию:
определяет
число молекул в единице объема, т.е.
концентрацию:
|
|
И для давления получаем выражение:
|
|
Это и есть основное уравнение молекулярно-кинетической теории газов. Ему можно придать другой вид, умножив и поделив правую часть на 2:
|
|
Здесь
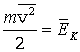 –
средняя кинетическая энергия одной
молекулы.
–
средняя кинетическая энергия одной
молекулы.
|
(2.5) |
Из последней формулы видно, что давление определяется количеством молекул в единице объема и их средней энергией поступательного движения.

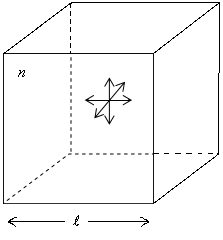 Рис.
2.5
Рис.
2.5