8.4. Повнота і замкненість

Ми розглянули два способи задання булевих функцій - таблич­ний і аналітичний. Таблиця задає функцію безпосередньо як відпо­відність між двійковими наборами і значеннями функції на цих набо­рах. Недолік табличного способу задания булевих функцій - громіздкість.

Формула - компактніший спосіб задания функції, проте вона задає функцію через інші функції. Тому для довільної системи функцій Qвиникає запитання: чи кожну булеву функцію можна зобразити формулою над Q? У попередньому параграфі отримана позитивнавідповідь на це запитання для системи. Справді, будь-яку булеву функцію можна зобразити досконалою ДНФ. Для функціїf, тотожно рівної нулю, маємо таке зображення: .

Покажемо, як розв'язати проблему для довільної системи буле­вих функцій Q.

8.4.1. Функціонально повні системи

Систему булевих функцій Qназивають функціонально повною, якщо довільну булеву функцію можна зобразити формулою надQ

Приклад 8.21.Розглянемо деякі повні системи.

1. Як уже було зазначено, система - повна.

2. Система {xу, х⊕у,1} - повна. Справді, якщо функція f≠0, то зобразимо її поліномом Жегалкіна; якщо f=0, то0=х⊕х.▲

Очевидно, що не кожна система булевих функцій є повною.Наприклад, система - неповна: через неї не можна зобрази­ти функцію двох змінних.

Дослідження повноти одних систем можна звести до дослід­ження повноти інших систем.

Теорема 8.7. Нехай задано дві системи булевих функцій Q_] та Q₂, причому система Q₁, функціонально повна і кожну її функцію можна виразити у вигляді формули через функції системи Q₂ . Тоді системаQ₂ також функціонально повна.

Доведення. Нехайf- довільна булева функція. Оскільки система Q₁повна, то функціюfможна виразити формулоюF₁, яка містить скінченну кількість функцій системи Q₂.Нехай це будуть функціїg₁, g₂, …, g_k. За умовою теореми кожна з цих функцій виражається формулою через скінченну кількість функцій системи Q₂ ,нехай це будуть функції h₁, h₂, …, h_l. Тому у формуліF можна усунути входження функційg₁, g₂, .., g_k, замінюючи їх формулами, які містять функції h₁, h₂, …, h_l. Тоді одержимо формулу F₂. Отже, функціюfвиразили у вигляді формули F₂ через функції h₁, h₂, …, h_l системи Q. Оскільки функціяfдовільна, то система Q₂ функціонально повна. ▲

Приклад 8.22.Продовжимо розгляд функціонально повних систем.

3. Система {х, ху} - повна, бо повною є система 1 іх∨у= .

4. Система 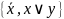- повна, тому що повною є система 1 і .

5. Система{х|у} є повною, тому що повною є система 3 і

8.4.2. Замкнені класи

Множину К булевих функцій називають замкненим класом, якщо довільна суперпозиція функцій із К знову належить К. Будь-яка системаQбулевих функцій породжує деякий замкнений клас. Цей клас складається з усіх функцій, які можна отримати суперпозиціями функцій ізQ,його називають замиканням Q.ЗамиканняQпозна­чають[Q].Очевидно, що якщо К - замкнений клас, то[К]=К, а якщоQ - функціонально повна система, то[Q]-P_r Існує п'ять найважливіших замкнених класів:

1. клас Т₀ функцій, що зберігають 0;

2. клас Т₁ функцій, що зберігають 1;

3. класSсамодвоїстих функцій;

4. клас М монотонних функцій;

5. класLлінійних функцій. Переходимо до вивчення цих класів.

Клас T₀ функцій, що зберігають 0. Булеву функціюf(x₁, …, x_n)називають функцією, яка зберігає 0, якщоf(0,..., 0)=0.

Наприклад, функції 0,x₁, x₁x₂, x₁∨x₂, x₁⊕x₂ зберігають 0, тобто належать класу Т₀, а функції 1, не зберігають 0, тобто не

належать класуT₀.Таблиця значень функції ізT₀у першому рядку

завжди має 0. Отже, в Т₀ є булевих функцій, якізалежать від змінних x₁, …x_n.

Теорема 8.8. Т₀ - замкнений клас. Іншими словами, із функцій, що зберігають 0, суперпозицією можна одержати лише функції, що зберігають 0.

Доведення. Клас Т₀ містить тотожну функцію. Отже, досить довести, що функція

зберігає 0, якщо функціїf, f₁, f₂, …, f_m зберігають 0. Справді, ▲

Наслідок. Повна система функцій повинна містити хоча б одну функцію, яка не зберігає 0. Іншими словами, повна система функцій не повинна цілком міститись у замкненому класі Т₀. ▲

КласТ₁ функцій, що зберігають1. Булеву функцію називають функцією, яка зберігає 1, якщоf(1,..., 1 )=1.

Наприклад, функції 1,x₁, x₁x₂, x₁∨x₂, x₁⊕x₂належить класуТ₁, а функції 0, не належать Т₁.

Теорема 8.9. Т₁ - замкнений клас.

Доведення. Т₁ містить тотожну функцію. Отже, достатньо довести, що функція

зберігає 1, якщофункціїf, f₁, f₂, …, f_m зберігають 1. Справді,

Наслідок. Повна система функцій повинна містити хоча б одну функцію, яка не зберігає 1. Іншими словами, повна система функцій не повинна цілком міститись у замкненому класі Т₁▲

Легко показати, що клас Т₁ має функцій, які залежать відn змінних х₁, …х_п. Зазначимо, що існують булеві функції, які збері­гають і 0, і 1, водночас є функції, які не зберігають ні 0, ні 1. Наприк­лад,

x₁x₂, x₁∨x₂, x₁⊕x₂⊕x₃ ∈T₀∩T₁, ax₁|x₂, x₁↓x₂∉T₀∪T₁.

Клас S самодвоїстих функцій.Нагадаємо означення самодвоїстої функції: функцію називають самодвоїстпою, якщо вона двоїста до самої себе: f *= f . Наприклад, функції x1, , x1⊕x2⊕x3- самодвоїсті, а функції x1x2, x1∨x2, 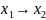несамодвоїсті. Використовуючи означення двоїстої функції, можна дати інше означення самодвоїстої функції, еквівалентне до попереднього означення.

Булевуфункцію називають самодвоїстою, якщо на протилежних наборах значень змінних вона приймає протилежнізначення: .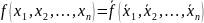

Звідси, зокрема, випливає, що самодвоїста функція повністю визначена своїми значеннями на першій половині наборів. Отже, кількість самодвоїстих функцій від п змінних дорівнює кількостідвійкових наборів довжини тобто .

Теорема 8.10. Клас S самодвоїстих функцій замкнений.

Доведення. Оскільки тотожна функція належить класу S, достат­ньо довести, що функція

самодвоїста, якщо функціїf, f₁, f₂, …, f_mсамодвоїсті. Використовуючи принцип двоїстості, отримаємо:

.▲

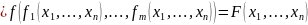Наслідок. Повна система булевих функцій повинна містити хоча б одну несамодвоїсту функцію. ▲

Теорема 8.11 (лема про несамодвоїсту функцію). Із несамодвоїстої функції f(x₁, …, x_n)підстановкою функцій xта можна отримати несамодвоїсту функцію однієї змінної, тобто константу.

Доведення. Нехайf(x₁, …, x_n) ∉S. Отже, існує принаймні один такий набір значень змінних, що

За набором визначимо допоміжні функції i=1, 2, …,n:

Легко переконатись, що ці функції мають властивість , (i=1, 2, …, n).

Розглянемо функцію Ф(x)= . Ця функція отримана з функціїf(x₁, …, x_n) підстановкою xта . Функція Ф(х) - конс­танта, оскільки

Клас М монотонних функцій. На множині всіх n-місних двійкових наборів уведемо відношення часткового порядку. Нехай , - двійкові набори; набір ,якщо a_n≤b_n для всіх i=1,2, ...,n. Наприклад, (010)≤( 110), а набори (010) і (100) порівняти не можна.

Функцію f(x₁, …, x_n) називають монотонною, якщо для будь-яких двійкових наборів із того, що випливає, що . Наприклад, 0, 1, х₁, х₁х₂, х₁∨х₂ – монотонніфункції, а - немонотонні.

Перевірка монотонності функцій безпосередньо за означенням вимагає аналізу таблиці функції і може виявитись досить громізд­кою. У багатьох випадках досить легко з'ясувати, що функція немонотонна.

Теорема 8.12.Нехай - монотонна функція. Якщо не зберігає 0, то вона тотожно дорівнює 1. Якщо не зберігає 1, то вона тотожно дорівнює 0.

Доведення. Для будь-якого набору виконується . Далі, 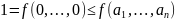Отже, для довільного набору , тобтоfє константою 1. Друге твердження теореми доводять аналогічно. ▲

Наслідок. Якщо функція f∈T₀∩T₁ і не є константою, то вона немонотонна.▲

Отже, всі монотонні функції, окрім констант 0 та 1, належать T₀∩T₁.Зауважимо, що існують функції, які належатьT₀∩T₁, але не є монотонними, наприклад,x₁⊕x₂⊕x₃.

Теорема 8.13.Клас М монотонних функцій замкнений.

Доведення. Оскільки тотожна функція належить класуМ, то для доведення замкненості Мдосить показати, що функція

монотонна, якщо функціїf, f₁, f₂, …, f_mмонотонні. Нехай ,тоді для всіх i=1,2,...,п. Звідси

Отже, ,

Наслідок. Повна система булевих функцій повинна містити хоча б одну немонотонну функцію. ▲

Теорема 8.14(лема про немонотонну функцію). Ізнемонотонної функції підстановкою констант 0, 1 та функції х можна отримати функцію .

Доведення.Нехайf(x₁,...,х_n)∉М,отже, існує два набори , значень зміннихх₁, ..., х_nтакі, що ,але ,тобто , .

Якщо та відрізняються у kкомпонентах, то в цих компо­нентах у наборі є нулі, а в наборі -одиниці (оскільки ).

Підставимо у функцій)/^,... ,xjзамість змінних, яким у наборах а" та В" відповідають однакові значення, просто ці значення, а на місце решти £ змінних - функціюх. Тоді отримаємо функцію однієї

змінноїg(x).Враховуючи, що , , одержимоg(0) = , . Отже,g(x)= . ▲

Клас Lлінійних функцій.Булеву функціюf(x₁, …, x_n)називають лінійною, якщо їїполіном Жегалкіна має вигляд

Це поліном першого степеня, або лінійний поліном. Він не має багатомісних кон'юнкцій вигляду х_i.х_j, х_iх_jх_k тощо.

Коефіцієнтиc₀, с₁,...,с_плінійного полінома утворюють довіль­ний набір значень із n+1 нулів та одиниць. Через єдиність полінома Жегалкіна різним наборам коефіцієнтів відповідають різні булеві функції. Отже, є точно 2ⁿ⁺¹ лінійних булевих функцій від n змінних. Прикладами лінійних булевих функцій є 0, 1,х, , х₁~х_2> а функції x₁→x₂, x₁∨x₂ - нелінійні.

Неважко переконатись, що серед лінійних функцій самодвоїсгими є ті, у яких поліном Жегалкіна містить непарну кількість змінних, а несамодвоїстими ті, у яких поліном Жегалкіна містить парну кількість змінних. Наприклад, функціїx, x⊕1, x₁⊕x₂⊕x₃- самодвоїсті, а функції x₁⊕x₂, x₁⊕x₂⊕1 -- несамодвоїсті.

Серед лінійних функцій монотонними є лише 0,1, x.

Теорема 8.15.КласіL лінійних функцій замкнений.

Доведення. МножинаLусіх лінійних функцій є замкненим класом, оскільки підстановка формул вигляду у формулу такого ж вигляду знову дає формулу того самого вигляду. ▲

Наслідок. Повна система булевих функцій повинна містити хоча б одну нелінійну функцію. ▲

Теорема 8.16(лема про нелінійну функцію). Якщо функція нелінійна, то існує зображення кон'юнкції двох змінних у вигляді суперпозиції констант 0 il,заперечення та функції

Доведення. Нехайf∉L.Тоді її поліном Жегалкіна містить кон'юнкції змінних. Виберемо серед них кон'юнкцію найменшого рангу, нехай це буде

Надамо значення , а для всіх x_j, які не входять в k, надамо значення x_j=0. Підстановка цих констант у поліном перетво­рить.решту кон'юнкцій - в 0. При цьому функція/набере вигляду , , деα, β, γ- коефіцієнти, що дорівнюють 0 або 1 і залежать від конкретної функції f(x₁,...,х_n).

Розглянемо функцію

Отже, .

Цю функцію отримано суперпозицією констант 0 il,заперечен­ня та функціїf(x₁,...,х_n)∉L.Якщо , то . Якщо , то .▲

8.4.3. Критерій функціональної повноти системи булевих функцій

Перейдемо безпосередньо до критерію функціональної повноти, який дає теорема про функціональну повноту, доведена Е. Постом (Е. Post) 1921 p.

Теорема 8.17. Для того, щоб система булевих функційQбула функціонально повною, необхідно й достатньо, щоб вона містила 1) функцію, яка не зберігає 0; 2) функцію, яка не зберігає 1; 3) несамодвоїсту функцію; 4) немонотонну функцію; 5) нелінійну функцію.

Іншими словами, для повноти системиQнеобхідно й достатньо, щоб для можного з п'яти замкнених класівT₀, T₁S, М, Lвона містила функцію, яка цьому класу не належить..

Доведення. Необхідність. Вона випливає із замкненості кож­ного з п'яти розглянутих класів (наслідки з теорем 8.8, 8.9, 8.10, 8.13,8.15).

Достатність. Уведемо позначення для функцій із системиQ:

f_i- функція, яка не зберігає 0;

f_j-функція, яка не зберігає 1;

f_k- несамодвоїста функція;

f_m - немонотонна функція;

f_l- нелінійна функція.

Доведення виконаємо в 2 етапи.

Перший етап. На цьому етапі одержимо константи 0 та 1. Роз­глянемо функціюf_i (не зберігає 0):f_i(0, ...,0)=1. Можливі два випадки.

1. f_i(1, ...,1)=1, тоді функція тотожно дорівнює 1, бо =1, .

Із функціїf_i(не зберігає 1) у цьому випадку можна одержати константу 0, тому що .

2. . Тоді функція є запереченням: , оскільки .

Із несамодвоїстої функціїf_k і побудованої функції за лемою про несамодвоїсту функцію (теорема 8.11) одержимо константу. Другу константу одержимо, використовуючи , оскільки , . Отже, у випадках 1) та 2) одержимо функції 0 та 1.

Другий етап. Використовуючи константи 0, 1 і немонотонну функцію f_m за лемою про немонотонну функцію (теорема 8.14) одержимо. Далі, використовуючи константи 0,1 і функції та f_l∉Lза лемою про нелінійну функцію (теорема 8.16) одержимо кон'юнкцію двох зміннихху.

Отже, через функції системи Qвиразили таху. Але система { ,ху} - повна. Отже, за теоремою 8.7 і система Q повна. ▲

Для перевірки виконання для деякої скінченної системи функцій {f₁, …, f_q} умов теореми Поста складають таблицю, яку називають таблицею Поста. Рядки цієї таблиці позначено функціями системи, а стовпці - назвами п'яти основних замкнених класів.

У клітках таблиці Поста ставлять знак "+" або "-" залежно від того, належить чи не належить функція замкненому класу. Для повноти системи функцій необхідно й достатньо, щоб у кожному стовпчику таблиці Поста був хоча б один "-"(мінус).

Приклад 8,23.Дослідимо, чи є функціонально повною система {х→у,0}. Побудувавши таблицю Поста (табл. 8.6), переконуємося, що ця система є функціонально повною. ▲

Таблиця 8.6

	T0	T1	S	M	L
x→y	-	+	-	-	-
0	+	-	-	+	+

Мінімальну повну систему функцій (тобто таку повну систему функцій, вилучення із якої довільної функції робить систему непов­ною) називають базисом. Із теореми Поста випливає, що базис не може містити більше п'яти функцій. Насправді, відомий точніший результат.

Теорема 8.18.Максимальна кількість функцій базису дорівнює 4.

Доведення. Функціяf_i∉Т₀або несамодвоїста:f_i(0, ..., 0)=f_i(1,..1)=1 (випадок 1 доведення теореми 8.17), або не зберігає 1 і немонотонна (випадок 2 доведення теореми 8.17).

Отже, повною буде або система {f_i, f_j, f_m, f_l}, або система {f_i, f_k, f_l}. Константу 4 у цій теоремі не можна понизити. Система з чотирьох функ­цій {f₁, f₂, f₃, f₄}, де f₁=0, f₂=2, f₃ =x₁x₂ , повна. Із цієї системи не можна вилучити жодної функції без порушення повноти. Справді, функціяf₁ є єдиною із функцій цієї системи, що не зберігає 1,f₂- єдиною функцією, що не зберігає 0,f₃- єдиною нелінійною функцією, f₄- єдиною немонотонною функцією. Несамодвоїстих тут три функції:f₁, f₂, f₃.▲