
- •Розділ 7 Основи теорії кодування План викладення матеріалу
- •7.1. Алфавітне й рівномірне кодування
- •7.2. Достатні умови однозначності декодування. Властивості роздільних кодів
- •7.3. Оптимальне кодування
- •7.4. Коди, стійкі до перешкод. Коди Хемінга
- •8.2. Алгебри булевих функцій
- •8.3. Спеціальні форми зображення булевих функцій в алгебрах Буля і Жегалкіна
- •8.3.1. Диз'юнктивні нормальні форми
- •8.3.2. Кон'юнктивні нормальні форми
- •8.3.3. Поліном Жегалкіна
- •8.4. Повнота і замкненість
- •8.4.1. Функціонально повні системи
- •8.4.2. Замкнені класи
- •8.4.4. Послаблена функціональна повнота
- •8.4.5. Передповні класи
- •8.5. Мінімізація булевих функцій
- •8.5.1. Основні результати
- •8.5.2. Методи побудови скороченої днф
- •8.5.3. Побудова тупикових днф
- •8.5.4. Властивості скороченої днф
- •8.5.5.Метод карт Карно побудови мінімальних днф
- •8.6. Реалізація булевих функцій схемами з функціональних елементів
- •Комп'ютерні проекти
- •Література
- •9.2. Формальні породжувальні граматики
- •9.3. Типи граматик (ієрархія Хомські)
- •9.4. Дерева виведення
- •9.5. Форми Бекуса-Наура
- •9.6. Скінченні автомати з виходом
- •9.7. Скінченні автомати без виходу
- •9.8. Подання мов
- •Комп'ютерні проекти
- •Література
- •Розділ 10
- •План викладення матеріалу
- •10.1. Основні вимоги до алгоритмів
- •10.2. Машини Тьюрінга
- •10.3. Обчислення числових функцій на машинах Тьюрінга
7.4. Коди, стійкі до перешкод. Коди Хемінга
У цьому параграфі розглянемо один
частковий випадок рівномірного двійкового
кодування, а саме, уважатимемо, що не
лише алфавіт В={0,1},
алейалфавітА={0,1}.
Розглянемосхему
рівномірного кодування
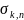 із параметрами k,
n:
із параметрами k,
n:

де
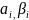 – слова
довжини,
відповідно,
n
та
k
(n
– слова
довжини,
відповідно,
n
та
k
(n ).
Кажуть,
щосхема
визначена кодом
).
Кажуть,
щосхема
визначена кодом
 .
.
Нормою двійкового
вектора α=
двійкового
вектора α= компонент. Отже,
компонент. Отже,

Операцію над двійковими розрядами (бітами)-
додавання
за модулем 2
(mod2)
– означуютьтак:
0
над двійковими розрядами (бітами)-
додавання
за модулем 2
(mod2)
– означуютьтак:
0 0=0
0=0
 .
Якщо α
та β–
двійкові вектори,то α
.
Якщо α
та β–
двійкові вектори,то α - порозрядне
додавання за модулем
2.
- порозрядне
додавання за модулем
2.
Припустимо,що
в каналі зв’язкудієджерелоадитивнихперешкод,
яке описуютьмножиноюP(n,t).
Елементи цієї множини – двійкові
вектори –помилки у яких норма будь-якого фрагмента,
у яких норма будь-якого фрагмента,
 не
більша,
ніжt,
якщодловжина фрагмента Ɩ≤n
(тобто на n переданих поспіль двійкових
символів припадає не більше, ніж
tпомилок).
Цеозначає,щоякщо
на вході
каналу зв’язку
передано повідомлення|α,
то на виходіможе бути отримано будь-яке
слово ізмножини
{α
не
більша,
ніжt,
якщодловжина фрагмента Ɩ≤n
(тобто на n переданих поспіль двійкових
символів припадає не більше, ніж
tпомилок).
Цеозначає,щоякщо
на вході
каналу зв’язку
передано повідомлення|α,
то на виходіможе бути отримано будь-яке
слово ізмножини
{α
Припустимо,
що в каналі зв'язку діє
джерело адитивних перешкод,
яке описують множиною
Р(п,і).
Елементи цієї множини - двійкові
вектори-помилки x1x2...xs,
у яких норма будь-якого фрагмента
xixi+1…xi+l-1
не більша, ніж t,
якщо довжина фрагмента l≤n
(тобто на n
переданих поспіль двійкових символів
припадає не більше, ніжt
помилок). Це означає, що якщо на вході
каналу зв'язку передано повідомлення
а, то на виході може бути отримано
будь-яке слово із множини {α .
.
Оскільки проблема локалізації інформації (розділення закодованого повідомлення на елементарні коди) у моделі рівномірного кодування тривіальна, то виявлення помилок полягає в знаходженні незбігу локалізованої групи п символів з жодним елементарним кодом. Якщо внаслідок помилки елементарний код перейде в інший елементарний код, то помилку не буде виявлено. Іноді можливе виправлення помилки. Якщо групу символів локалізовано правильно, то для цього необхідно й достатньо, щоб помилкова група була "синонімом" єдиного елементарного коду.
Канал зв'язку називають надійним, якщо будь-які помилки виявляються або виправляються відповідно до заданої мети декодування. Далі наведені головні положення побудови кодів, які забезпечують надійність найпростіших каналів зв'язку.
З методичних міркувань у цьому параграфі зручно використовувати такі позначення. Елементи множини - двійкові вектори довжини п ~ позначатимемо великими латинськими буквами X,Y,Z, а їхні компоненти - відповідними малими буквами з індексами. Зокрема, елементарні коди будемо позначати як традиційно β1, β2, β3,…, так і X,Y,Z, залежно від контексту.
Віддаллю Хемінга називають функціюр(Х,Y) двох змінних, визначену на множині Е
: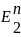 :
ρ(X,Y)=
:
ρ(X,Y)= (дорівнює кількості розрядів, у яких
вектори Xта
У не збігаються).
Скалярний добутоквекторів
Х,Y∈
Е
(дорівнює кількості розрядів, у яких
вектори Xта
У не збігаються).
Скалярний добутоквекторів
Х,Y∈
Е визначають так:
визначають так: .
Він дорівнюєкількості розрядів, у яких
X
та Y
збігаються й дорівнюють 1.
.
Він дорівнюєкількості розрядів, у яких
X
та Y
збігаються й дорівнюють 1.
Легко перевірити такі співвідношення:

де 0 (виділено напівжирним шрифтом) - n-вимірний вектор із нульовими компонентами,
 ,
(7.2)
,
(7.2)
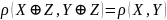 (7.3)
(7.3)
 (7.4)
(7.4)
Для віддалі Хемінга виконуються аксіоми метрики:
 ,
причому
,
причому в тому й лише в тому випадку, якщо
Х = У;
в тому й лише в тому випадку, якщо
Х = У;

та
нерівність трикутника
Метрика
Хемінга є зручним математичним поняттям
для формулювання умов надійності
кодування в разі адитивних помилок.
Нехай схемаσk,п
визначена кодом .Кодовоювіддаллю
для коду
V
називають величину
.Кодовоювіддаллю
для коду
V
називають величину

Теорема 7.7. Якщо в каналі зв'язку діє джерело адитивних перешкодP(n,t)то
для виявлення будь-яких помилок необхідно й достатньо p(V)>t;
для виправлення будь-яких помилок необхідно й достатньо p(V)>2t.
Зауваження. Іншими словами, код здатний виявляти будь-які комбінації зt і меншої кількості помилок тоді й лише тоді, коли його кодова віддаль більша ніжt; код здатний виправляти будь-які комбінації зt і меншої кількості помилок тоді й лише тоді, коли його кодова віддаль більша ніж 2t.
Доведення.
1. Нехай ρ(V)>t.
Якщо
Х∈
V, Z∈P(n,t),
Z≠0,то,
використовуючи спочатку (7.3), а потім
(7.1), можемо записати
 .
Отже, X⊕Z∈
Vi
помилку виявлено. Навпаки, нехай𝜌(Х,
Y)≤t
таX,Y∈V,X≠Y.
Тоді, використовуючи (7.2), маємо
.
Отже, X⊕Z∈
Vi
помилку виявлено. Навпаки, нехай𝜌(Х,
Y)≤t
таX,Y∈V,X≠Y.
Тоді, використовуючи (7.2), маємо
 ,
отже,
Z=X⊕Y∈P(n,t).
Звідси випливає, щоX⊕Z=Y,тобто
помилку в елементарному кодіYне
можна виявити.
,
отже,
Z=X⊕Y∈P(n,t).
Звідси випливає, щоX⊕Z=Y,тобто
помилку в елементарному кодіYне
можна виявити.
2. Нехай ρ(V)>2t.
Якщо
Х∈
V,Z∈Р(п,t),
то
Х є
єдиним елементарним кодом з
V,
який міг перейти внаслідок помилки
вX⊕Z.
Справді, припустимо, що існує Y≠X
такий, щоY∈
V таY⊕Z1=X⊕Z
для деякого Z1∈P(n,t).
Додамо до обох частин останньої
рівностіX⊕Z1тоді
отримаємоX⊕Y=Z1⊕Z.Але,
використовуючи (7.2), можемо записати ,
a
,
a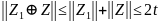 .
Суперечність. Навпаки, нехай𝜌(Х,
У)<2t
для деяких різних
X,
Y∈V,
тоді
.
Суперечність. Навпаки, нехай𝜌(Х,
У)<2t
для деяких різних
X,
Y∈V,
тоді
 .
Отже існують, Z1
та Z2
такі, що
.
Отже існують, Z1
та Z2
такі, що
 ,
,
 (тобто Z1,
Z2∈
P(n,t))
таX⊕Y=Z1⊕Z2.
ЗвідсиX⊕Z1=Y⊕Z2=W,
тобто в разі отримання спотвореного
елементарного кодуW
неможливо визначити,Xчи
Yбув
переданий насправді.
▲
(тобто Z1,
Z2∈
P(n,t))
таX⊕Y=Z1⊕Z2.
ЗвідсиX⊕Z1=Y⊕Z2=W,
тобто в разі отримання спотвореного
елементарного кодуW
неможливо визначити,Xчи
Yбув
переданий насправді.
▲
Доведений результат має геометричну інтерпретацію.
МножинуSt (X) = {У|ρ(X, У) ≤ t} називають кулею радіуса t із центром у точці X.
Теорема 7.8. Якщо в каналі зв'язку діє джерело адитивних перешкодP(n,t) то
для виявлення будь-яких помилок необхідно й достатньо, щоб для будь-якого Х,Y∈ V куляS1(X)не містила інших елементарних кодів, крім X;
для виправлення будь-яких помилок необхідно й достатньо, щоб для будь-яких Х,Y∈ V виконувалась умоваSt(X)∩St(Y) =∅.▲
Рівномірне
кодування σk,n
: αi→βi(i=1,2,3,...,2k)
називають систематичним,
якщо можна виділити множину
к
розрядів
 ,
які називають
інформаційними,
так, що коли
,
які називають
інформаційними,
так, що коли
 (i=1,2,3,...,2k),
то
(i=1,2,3,...,2k),
то
 .
Решту розрядів у такому разі називають
контрольними.
.
Решту розрядів у такому разі називають
контрольними.
Рівномірне
кодування σk,n:
α→ βi
(i=1,2,3,...,2k)
називаютьлінійним,
або
груповим,
якщо код
утворює
підгрупу відносно операції ⊕
порозрядного додавання векторів за
модулем
два. У такому разі код V
є одночасно
лінійним підпростором простору
над полем Е2.
Усі лінійні коди - систематичні.
відносно операції ⊕
порозрядного додавання векторів за
модулем
два. У такому разі код V
є одночасно
лінійним підпростором простору
над полем Е2.
Усі лінійні коди - систематичні.
Лінійні коди можна задавати простіше, ніж коди загального типу. Достатньо вказати твірні групи V. Їх можна подати матрицею з k рядками та п стовпцямиG(V) -- базисом векторного простору V. МатрицюG(V) називаютьпороджувальною матрицею коду V. За допомогою породжувальної матриціG=G(V) можна кодувати повідомлення. Якщо - повідомлення, то β=αG.
Двоїстість,
яка зв'язує ортогональні підпростори,
приводить до ще одного способу задания
лінійних кодів. Вектори
Х,У∈ називають
ортогональними,
якщо
називають
ортогональними,
якщо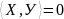 (mod2).
Ортогональний підпростірдля лінійного
коду
V
називають двоїстим
кодом
для
V.
Його розмірність дорівнює
п-k,
і
код
(mod2).
Ортогональний підпростірдля лінійного
коду
V
називають двоїстим
кодом
для
V.
Його розмірність дорівнює
п-k,
і
код визначає
двоїсту схему
алфавітного кодування σn-k,
n
. Матрицю
визначає
двоїсту схему
алфавітного кодування σn-k,
n
. Матрицю
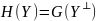 --
породжувальну матрицю коду
--
називаютьперевірною
матрицею
коду
V.
Отже, маємо
--
породжувальну матрицю коду
--
називаютьперевірною
матрицею
коду
V.
Отже, маємо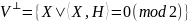 --двоїстий
спосіб задания лінійного коду V перевірною
матрицею Н=Н( V).
Легко переконатись, що якщо С(V)=[JkA] де
–Jk
одиничнаk×k-матриця;
то
--двоїстий
спосіб задания лінійного коду V перевірною
матрицею Н=Н( V).
Легко переконатись, що якщо С(V)=[JkA] де
–Jk
одиничнаk×k-матриця;
то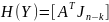 ,
де AT
--транспонована
матриця. Звідси випливає, що коли
І-множина
інформаційних розрядів для коду V,
то як
множину
інформаційних розрядів для двоїстого
коду V⊥
можна взяти
,
де AT
--транспонована
матриця. Звідси випливає, що коли
І-множина
інформаційних розрядів для коду V,
то як
множину
інформаційних розрядів для двоїстого
коду V⊥
можна взяти
 .
.
Приклад 7.7. Для лінійного коду V={000,011,101,110}, який визначає схему лінійного рівномірного кодування σ2,3
00→000,01→011,10→101,11→110
з інформаційними розрядами I={1,2}, маємо

і двоїсту схему σ1,3:
0→000, 1→111. ▲
Теорема 7.9. Для кодової віддалі лінійного коду виконується рівність
 (7.5)
(7.5)
Доведення. Зазначимо, що нульовий вектор 0 міститься в будь- якому лінійному коді. Рівність (7.5) випливає з того, що
 ▲
▲
P. Хемінг(R. Hamming) 1950 p. запропонував коди для виявлення й виправлення помилок у разіt=1. Коди Хемінга лінійні та мають найменшу надлишковість, можливу для даногоk.
Коди ХемінгаHdetect(n) для виявлення помилок у каналі зв'язку із джерелом перешкодP(n,1)визначені для будь-якого п:

КодHdetect(n) -- лінійний. Справді, якщоХ, Y∈Hdetect (n), то

ТобтоX⊕Y∈Hdetect (n).Заспіввідношенням (7.5) ρ(Hdetect (n))=2, тому, будь-якапомилкавканалізджереломперешкодР(n,1) виявляється. Як інформаційні розряди для коду Hdetect (n)можна взяти будь-які п-1 розрядів, оскільки значення в довільному розряді слова х1х2...хn∈НHdetect(n) однозначно визначається зазначеннями в інших розрядах із рівняння х1⊕х2⊕...⊕хn=0. Маємо

Як одну з породжувальних матриць можна взятии

ЯкщовибратиI={ 1, 2, j, n-1}, тоотримаємовідповіднусхемурівномірногокодування σn-1,n:
x1x2…xn-1→x1x2…xn-1xn,
де xn=х1⊕х2⊕...⊕хn-1НадлишковістьуразівикористанняHdetect(n) становить R=(n-1)-1.
У цьому коді Хемінга найбільш явно використана ідея перевірки на парність.
Коди Хемінга для виправлення помилок у каналі зв'язку з джерелом перешкод Р(п, 1) будуються для значень п = 2s-1(s=2, З,...). Код (n) зручно задавати перевірною матрицею, яка має s рядків та 2s-1 стовпців. Стовпцями є всеможливі ненульові двійкові набори довжини s. Їх зручно розташовувати так, щоб i-й злівa стовпчик к був двійковим розкладом числа і (старші розряди зверху):

Таке розташування стовпців перевірної матриці зумовлено вибором як контрольних тих розрядів, у яких номери є степенями двійки: {1, 2,4,8,16,... ,2s-1}.
Приклад 7.8. Для значейьn=3,7 матимемо такі перевірні матриці коду Нсоrreсt(n):

 ▲
▲
За допомогою перевірної матриці Н=H(Нсоrreсt (п))код ХемінгаНсоrreсt (п) задають так:

 (7.6)
(7.6)
Приклад 7.9. Закодуємо повідомлення 1001 за допомогою коду Хемінга для n=7. Запишемо макет коду, беручи до уваги розташування контрольних розрядів:x1x2lx4001. Для знаходження значень контрольних розрядів використаємо умову (7.6) (доданки з нульовими коефіцієнтами не записані):

звідки х4⊕1=0, х2⊕1⊕1=0, х1⊕1⊕1=0. Отже, х1=0, х2=0, х4=1 і отримаємо такий код заданого повідомлення: 0011001. ▲
Покажемо,
що ρ
(Нсоrreсt(n))≥3,
тобто Нсоrreсt(n)забезпечує
корекцію будь-яких помилок у каналі
зв'язку з джерелом перешкодР(п,1).
Справді,
якщоХ≠0таХ∈Нсоrreсt(n),
то
 ,
оскільки всі стовпці перевірної матриці
ненульові. Далі,
,
оскільки всі стовпці перевірної матриці
ненульові. Далі,
 ,
оскільки якщо X
має одиниці лише в двох розрядах,
нехайхi=хj=1,
тоhi⊕hj
= 0, що є рівносильним hi=hj
а всі стовпці перевірної матриці різні.
Отже, найменша вага ненульового вектора
з Нсоrreсt(n)не
менша трьох. Тоді на підставі (7.5) ρ
(Нсоrreсt(n))≥3.
,
оскільки якщо X
має одиниці лише в двох розрядах,
нехайхi=хj=1,
тоhi⊕hj
= 0, що є рівносильним hi=hj
а всі стовпці перевірної матриці різні.
Отже, найменша вага ненульового вектора
з Нсоrreсt(n)не
менша трьох. Тоді на підставі (7.5) ρ
(Нсоrreсt(n))≥3.
Нехай в елементарному кодіX∈Нсоrreсt(n) виникла помилка в i-му розряді: кодХ=x1x2…xi…хп перейшов у код Х´=Х⊕еi=х1х2...хi⊕1…хп(тут еi— вектор, i-та компонента якого дорівнює 1, а решта компонент - нулі).
Тоді
 ,
бо
,
бо
 (mod
2). Звідси випливає, що коли локалізовано
послідовність символів
(mod
2). Звідси випливає, що коли локалізовано
послідовність символів
 , то достатньо визначити вектор
, то достатньо визначити вектор
 (mod2).
Якщо він нульовий, то помилки немає, а
ні, то цей вектор являє собою двійковий
розклад номера розряду, у якому виникла
помилка.
(mod2).
Якщо він нульовий, то помилки немає, а
ні, то цей вектор являє собою двійковий
розклад номера розряду, у якому виникла
помилка.
Приклад 7.10. Нехай для п=7 локалізовано послідовність X=0110010. Знаходимо

Робимо висновок, що виникла помилка в сьомому розряді елементарного коду, виправляємо її (інвертуємо помилковий розряд): 0110011. З відкоректованого коду виділяємо інформаційну групу розрядів (третій, п'ятий, шостий та сьомий розряди). У результаті отримуємо 1011. ▲
Надлишковість у разі використання коду Нсоrreсt(n) зменшується зі зростанням n:

Якщо ,
то будуютьукорочений
код Хемінга.
Його задають перевірною матрицею,
утвореною першимип
стовпцями перевірної матриці Нсоrreсt(n),
деп1
- найменше ціле із чисел, які більші ніжп
і мають вигляд 2s-1.
Очевидно, що всі попередні міркування
є правильними й для вкороченого коду
Хемінга.
,
то будуютьукорочений
код Хемінга.
Його задають перевірною матрицею,
утвореною першимип
стовпцями перевірної матриці Нсоrreсt(n),
деп1
- найменше ціле із чисел, які більші ніжп
і мають вигляд 2s-1.
Очевидно, що всі попередні міркування
є правильними й для вкороченого коду
Хемінга.
Задачі
Нехай числа 1, 2, 4, 17, 98 закодовані своїми двійковими розкладами мінімально можливої довжини. Наприклад, кодом одиниці є 1, кодом двійки є 10, кодом четвірки є 100. Чи є це кодування роздільним?
Для кожного з роздільних кодівV побудувати префіксний код із тим самим набором довжин елементарних кодіва-в:
а)V={01,10,100, 111,011};
б)V={1,10,00,0100};
в)V={10,101,111,1011}.
Для заданих розподілів імовірностей а - е появи букв побудувати коди за методом Фано:
а)Р={0.6, 0.1, 0.09,0.08, 0.07, 0.06};
б) Р={0.4, 0.4, 0.1, 0.03, 0.03,0.02, 0.02};
в) P={0.3, 0.2, 0.2, 0.1, 0.1, 0.05, 0.05};
г) P={0.25, 0.2, 0.15, 0.15, 0.15, 0.1};
д) P={0.4, 0.18, 0.1, 0.1, 0.07, 0.06, 0.05, 0.04};
е)P={0.2, 0.2, 0.19, 0.12, 0.11, 0.09,0.09}.
Для
кожного розподілу визначити
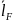 .
.
Для розподілів імовірностей а - е задачі 3 побудувати оптимальні коди за методом Хаффмана. Для кожного розподілу визначити
 та порівняти з відповідним значенням
(див.
задачу 3). Указати розподіли, для яких
метод Фано не дає оптимального коду.
та порівняти з відповідним значенням
(див.
задачу 3). Указати розподіли, для яких
метод Фано не дає оптимального коду.Якщо ймовірності появи букв є степенями двійки
 ,
то
довжини відповідних елементарних
кодів, одержаних за методами Фано і
Хаффмана, збігаються й дорівнюють
пi.Довести.
,
то
довжини відповідних елементарних
кодів, одержаних за методами Фано і
Хаффмана, збігаються й дорівнюють
пi.Довести.Використовуючи алгоритм Хаффмана, стиснути текст а, б. Визначити коефіцієнт стиснення (вважати, що в нестисненому тексті кожний символ кодують одним байтом):
а) THIS IS A SIMPLE EXAMPLE OF HUFFMAN ENCODING;
б)МІНІМІЗАЦІЯ ЧАСУ ВИКОНАННЯ ПРОГРАМИ.
Використовуючи код ХемінгаHdetect (n) для значення параметра n=8, закодувати повідомлення 011011110011010111101.
Повідомлення закодоване за допомогою коду ХемінгаHdetect(8). На виході каналу зв'язку з джерелом адитивних перешкод Р(8,1) отримано код 011010011001010011101110. Чи можна стверджувати, що під час його передавання виникла помилка? Якщо так, то в якій групі цифр?
Для повідомлень 1101 та 1011 побудувати код ХемінгаНсоrreсt(7), використовуючи перевірну матрицю Н.
Зауваження. Код ХемінгаНсоrreсt (7) часто називають (7,4)-кодомХемінга.
За допомогою коду ХемінгаНсоrreсt (7) закодувати повідомлення 110010111011. Для кодування використати перевірну матрицю H.
На виході каналу зв'язку з джерелом адитивних перешкод Р(7,1) отримано такі комбінації в коді ХемінгаНсоrreсt (7):
а) 1001001; б)0110001; в) 0011111; г) 0110100.
Виконати корекцію кодів і декодувати ці повідомлення.
Знайти породжувальну матрицю G=G(Нсоrreсt (7)) коду ХемінгаНсоrreсt(7).
Для повідомлень 1101 та 1011 побудувати код ХемінгаНсоrreсt(7), використовуючи породжувальну матрицю G (див. задачу 12).
За допомогою коду ХемінгаНсоrreсt(7) закодувати повідомлення 110010111011. Для кодування використати породжувальну матрицю G (див. задачу 12).
Побудувати код Хемінга для виправлення помилки в одному розряді, і виявлення помилки в двох розрядах під час передавання 4-розрядної двійкової комбінації. Записати перевірну матрицю цього кеду.
Вказівка. Використати код ХемінгаНсоrreсt(7), додаючи розряд к0 перевірки на парність (розширений (8,4)-кодХемінга, див. зауваження до задачі 9).
Під час передавання за розширеним кодом Хемінга отримані повідомлення: а) 00100001; б) 00110001. Що можна стверджувати у випадках а та б?
Побудувати код ХемінгаНсоrreсt(15) для передавання 11-розрядної інформаційної комбінації 10110110110. Показати процес виявлення помилки, яка відбулася в п'ятому розряді коду, отриманого на виході каналу зв'язку.
Зауваження. Код ХемінгаНсоrreсt(15) називають також (15,11)- кодом Хемінга.
Комп'ютерні проекти
Задано повідомлення. Закодувати його за методом Фано.
Задано повідомлення. Закодувати його за методом Хаффмана.
Задано схему алфавітного кодування й код повідомлення. Декодувати це повідомлення.
Задано повідомлення. Закодувати його за допомогою (7,4)- коду Хемінга (див. зауваження до задачі 9).
Для передавання повідомлення в каналі зв'язку з джерелом перешкод Р(7, 1) використано (7, 4)-кодХемінга. Задано код; домлення (можливо, з помилками, зумовленими властивос каналу зв'язку). Декодувати це повідомлення.
Задано розширений (8,4)-кодХемінга (див. задачу 15)Скласти програму, яка виявляє дві й виправляє одну помилку на кожні 8 переданих бітів. У випадку виявлення двох помилок видається відповідне повідомлення, а в разі однієї помилки здійснюється корекція коду й декодування.
Література
Андерсон Д. Дискретная математика и комбинаторика. - СПб.: Вильяме, 2003.
Ахо А., Хопкрофт Дж., Ульман Дж. Структурыданных и алгоритмы. - СПб.: Вильяме, 2000.
Гаврилов Г. П., Сапоженко А. А. Сборник задач по дискретнойматематике. - М.: Наука, 1977.
Липский В. Комбинаторика для программистов.—М.: Мир, I 1988.
Марков А. А. Введение в теориюкодирования. - М.: Наука, 1982.
Яблонский С. В. Введение в дискретную математику. - М.: Наука, 1986.
РОЗДІЛ 8
Булеві функції
План викладення матеріалу
8.1. Ознайомлення булевої функції. Реалізація функцій формулами.
8.2. Алгебри булевих функцій.
8.3. Спеціальні форми зображення булевих функцій в алгебрах Буля і Жегалкіна.
8.3.1.Диз'юнктивні нормальні форми.
8.3.2. Кон'юнктивні нормальні форми.
Поліном Жегалкіна.
Повнота і замкненість.
8.4.1. Функціонально повні системи.
Замкнені класи.
Критерій функціональної повноти системи булевих функцій.
Послаблена функціональна повнота.
Передповні класи.
Мінімізація булевих функцій.
Основні результати.
Методи побудови скороченої ДНФ.
Побудова тупикових ДНФ.
Властивості скороченої ДНФ.
Метод карт Карно побудови мінімальних ДНФ.
Реалізація булевих функцій схемами з функціональних елементів.
Задачі.
Комп 'ютерні проекти.
Література.
8.1. Означення булевої функції.
Реалізація функцій формулами
Булевою називають функцію ƒ(x1,…,xn)область значень якої складається з 0 та 1, і яка залежить від змінних х1,..., хn, що приймають також лише ці два значення.
Множину всіх булевих функцій позначають Р2.Булеві функції широко застосовують у математичній і технічній кібернетиці, зокрема, для конструювання мікропроцесорів.
Булеву
функцію відnзмінних
називаютьп-місною.
Областю її визначення є множина
усіх можливих n-місних
наборів (векторів) значень змінних.
Ці набори називають
двійковими наборами, або
просто
наборами.
Отже, область визначення n-місної
булевої функції є скінченною і складається
з2п
наборів значень змінних. Для набору
(а1,
..., ап)
використовують позначення
 або
або .
.
Щоб зробити викладення цього розділу незалежним, сформулюємо ще раз деякі означення.
Нормою
набору
називають
число ,
що дорівнює кількості його одиничних
компонент.
,
що дорівнює кількості його одиничних
компонент.
Віддаллю
Хемінга між наборами
та
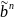 називають число
називають число

Це
число дорівнює кількості компонент, у
яких набори
та
відрізняються.
Набори
та
називають сусідніми, якщо
 і
протилежними, якщо
і
протилежними, якщо .
Отже, сусідні набори відрізняються в
одній компоненті, а протилежні - в усіх
n
компонентах. Наприклад, набори (0100) та
(1100) - сусідні, а (0100) та (1011) - протилежні.
.
Отже, сусідні набори відрізняються в
одній компоненті, а протилежні - в усіх
n
компонентах. Наприклад, набори (0100) та
(1100) - сусідні, а (0100) та (1011) - протилежні.
Скінченність області визначення довільної булевої функції дає змогу задавати таку функцію таблицею. Розташуємо всі набори значень змінних у стовпчик у лексикографічному порядку і вкажемо значення функції на кожному з них Тоді одержимо таблицю булевої функції (див. табл. 8.1).
Правий стовпчик цієї таблиці (стовпчик значень функції) складається з2п нулів та одиниць. Отже, n-місних булевих функцій існує стільки, скільки існує наборів довжини2n з 0 та 1. Томуправильнішє наступне твердження.
Таблиця 8.1
x1, x2, …, xn-1,xn |
f(x1, x2, …, xn-1, xn) |
0 0 . . . 0 0 0 0 . . . 0 1 0 0 . . . 1 0 …………. 1 1 . . . 1 1 |
f(0, 0, ..., 0, 0) f(0, 0, ..., 0, 1) f(0, 0, ..., 1, 0) …………….... f(1, 1, ..., 1, 1) |
Теорема8.1.
Кількість p2(n)
всіх функцій з
Р2
які залежать від n змінних х1,.
..., xn
дорівнює
 .
▲
.
▲
Далі
завжди будемо передбачати лексикографічне
розташуванні наборів. Тому функцію
 можна задавати вектором
можна задавати вектором ,
у якому компонента
,
у якому компонента
 є значення функції
є значення функції
 наi-му
наборі значень змінних, i=0,1,
...,2n-1.
наi-му
наборі значень змінних, i=0,1,
...,2n-1.
Множину
наборів значень змінних, на яких булева
функція приймає значення 1, позначають Nf:
приймає значення 1, позначають Nf:

Множина ,
очевидно, повністю визначає функціюf.
,
очевидно, повністю визначає функціюf.
Зміннухi
функції
 ,
називають
істотною, якщо
існує такий набір
,
називають
істотною, якщо
існує такий набір значень
решти змінних, що
значень
решти змінних, що

Змінну, яка істотною не є, називаютьнеістотною,або фіктивною. Отже, змінна хi функції неістотна (фіктивна), якщо

для
довільних значень решти змінних. Це
означає, що зміна знамення
 в довільному наборі значень
в довільному наборі значень не змінює значення функції.
У цьому випадку функція
не змінює значення функції.
У цьому випадку функція
 по
суті залежить від (n-1)
змінної, тобто є функцією
по
суті залежить від (n-1)
змінної, тобто є функцією
 .
У такому разікажуть, що функція g отримана
із функціїfвилученням
фіктивної змінної,
а функція f
отримана ізg
уведенням
фіктивної змінної.Функції
fта
g
називають
рівними,
якщо функцію
g
можна отримати з f
шляхом уведення або вилучення фіктивних
змінних.
.
У такому разікажуть, що функція g отримана
із функціїfвилученням
фіктивної змінної,
а функція f
отримана ізg
уведенням
фіктивної змінної.Функції
fта
g
називають
рівними,
якщо функцію
g
можна отримати з f
шляхом уведення або вилучення фіктивних
змінних.
Мета вилучення фіктивних змінних полягає в тому, що вони не впливають на значення функції, і з цієї точки зору є зайвими. Проте, іноді буває корисним уводити фіктивні змінні. Завдяки цьому довільну функцію п змінних можна зробити функцією довільної більшої кількості змінних. Тому, якщо задана скінченна множина булевих функцій {f1,..., fs}9 то можна вважати, що всі ці функції залежать від одних і тих самих змінних x1,...,хп. Зокрема, твердження, що всіх и-місних булевих функцій є передбачає, що беруть до уваги всі булеві функції від n змінних, у тому числі й функції з фіктивними змінними.
Із
ростом кількості змінних швидко
збільшується кількість залежних від
них булевих функцій. Наприклад, різних
булевих функцій чотирьох змінних є
 тис., а п'яти --
тис., а п'яти --
 млрд. Зі збільшенням кількості змінних
таблиці для булевих функцій стають
громіздкими і ними незручно користуватись.
млрд. Зі збільшенням кількості змінних
таблиці для булевих функцій стають
громіздкими і ними незручно користуватись.
Таблиця 8.2
-
x
0
1
x

0
1
0
0
1
1
0
1
1
0
Таблиця 8.3
x1 x2 |
x1x2 |
x1∨x2 |
x1→x2 |
x1∼x2 |
x1⊕x2 |
x1|x2 |
x1↓x2 |
0 0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
Розглянемо аналітичний метод задания булевих функцій, тобто задания функцій формулами. Спочатку за допомогою табл. 8.2 та 8.3 визначимо функції, які називаютьлементарними.
Уведені елементарні функції мають такі назви.
f1(х)=0 - константа 0.
f2(х)=1 - константа 1.
f3(х)=х - тотожна функція.
f4(х) =
 -заперечення
х, читають "не х".
-заперечення
х, читають "не х".f5(х1, х2)=х1х2-- кон'юнкція, читають "х1 і х2". Іноді для кон'юнкції використовують символи ∧ та &.
f6(х1, х2=х∨х2 -диз'юнкція, читають "х1 або х2".
f7(х1, х2)= х1→х2 -імплікація, читають "із х1 випливає х2". Для імплікації іноді використовують символ ⊃.
f8(х1, х2)=х1∼х2--еквівалентність. Для її позначення використовують також символ ≡.
f9(х1, х2)= х1⊕х2 --додавання заmod2, читають як альтернативне "або" ("або..., або")
f10(х1, х2)=х1|х2 --штрих Шеффера.
f11(х1, х2)= х1↓х2 -стрілка Пірса.
За допомогою елементарних функцій можна зобразити будь-яку булеву функцію в аналітичній формі, тобто у вигляді формули. Для булевих функцій f1 , ..., fm, по-перше, можливі будь-які підстановки одних функцій замість змінних в інші функції. По-друге, можливі будь-якіперейменування змінних, наприклад, перейменування x3 в х2 породжує з функціїf(хі,х2,х3,х4) функцію трьох змінних f(хі,х2,х3,х4) (у такому разі кажуть, що змінні х2 та х3ототожнені). Функцію, що одержана з f1 , ..., fm деякою підстановкою їх одна в одну й перейменуванням змінних, називаютьсуперпозицієюf1 , ..., fm. Вираз, який описує суперпозицію та містить функціональні символи, круглі дужки та символи змінних, називають формулою.
Приклад
8.1.
Тримісна булева функція задана формулою.
Вона є суперпозицією функцій
формулою.
Вона є суперпозицією функцій
f7(х1, х2)= х1→х2, f4(х) = , f9(х1, х2)= х1⊕х2. ▲
Формулу, яка містить лише змінні, дужки й символи функцій із множиниQназиваютьформулою над Q.
Приклад
8.2.
НехайQ={
,ху,
х∨у},
тоді вираз
 є
формулою надQ.▲
є
формулою надQ.▲
З метою зменшення кількості дужок у формулах уводять пріоритет операцій, які визначені відповідними функціями: 1) заперечення; 2) кон'юнкція; 3) усі інші операції. Крім того, уводять домовленість, що символ заперечення відіграє роль дужок, якщо він є над частиною формули
Приклад
8.3.
Функція задана формулою .
Задамо
її таблицею. Процес розв'язування цієї
задачі наведено у табл. 8.4. ▲
.
Задамо
її таблицею. Процес розв'язування цієї
задачі наведено у табл. 8.4. ▲
Таблиця 8.4
-
x y z
xz
y⊕xz


0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
0
0
0
0
0
1
0
1
0
0
1
1
0
1
1
0
1
0
1
0
1
0
1
0
0
1
1
0
0
0
1
1
1
1
1
1
0
0
0
0
0
1
1
0
1
1
1
1
Про формулу, яка задає функцію, кажуть також, що вона реалізує або зображає цю функцію.
На відміну від табличного, зображення функції формулою не єдине. Формули називають еквівалентними або рівносильними, якщо вони реалізують рівні булеві функції. Еквівалентність формул позначають символом =.
Приклад 8.4. Формули х→y та( ∨у)∨z еквівалентні: х→y=( ∨у)∨z . У цьому можна переконатись, побудувавши таблиці відповідних булевих функцій. Очевидно, змінна z у другій формулі фіктивна. ▲
Крім побудови таблиць є інший метод доведення еквівалентності формул - рівносильні (еквівалентні) перетворення.
