9.2. Формальні породжувальні граматики

У лінгвістиці природних мов терміни "речення" й "слово" мають різний смисл; тому в математичній лінгвістиці послідовність сим­волів звичайно називають нейтральним терміном "ланцюжок" (string), а мову, яку розуміють як множину формальних ланцюжків, - формальною мовою.

Формальна породжувальна граматика G(у подальшому грама­тика G)- це формальна система, визначена четвіркою об'єктів G=(V,T,S,P),де V— скінченна непорожня множина, яку називають алфавітом (або словником); T-її підмножина, елементи множини Т називають термінальними (основними) символами;S— початковий символ(S∈V), Р - скінченна множина продукцій (або правил перетворення) вигляду ξ→η, де ξ таη — ланцюжки в алфавіті V.

МножинуV\TпозначаютьN,її елементи називають нетермінальними (допоміжними) символами.

Формальні породжувальні граматики часто називають грамати­ками з фразовою структурою(phrase-structuregrammar),грамати­ками безпосередніх складових. Термінальні символи часто нази­вають терміналами, а нетермінальні символи - нетерміналами.

У теорії формальних граматик усталилися традиції позначень, яких будемо дотримуватись. Символи термінального алфавіту прийнято позначати малими латинськими буквами або цифрами, символи нетермінального алфавіту - великими латинськими буква­ми, ланцюжки в алфавіті V— грецькими буквами. Довжину ланцюжкаα позначають l(α) або |α|. Нагадаємо, що множину всіх ланцюж­ків в алфавіті V позначають V^*.

Нас цікавитимуть ланцюжки, які можуть бути породжені про-дукціями граматики.

Нехай G=(V,T,S,P)- граматика, і нехай α₀=σξτ, ξ≠λ (тобто α₀ – конкатенаціяσ, ξтаτ) та α₁=σητ - ланцюжки над V. Якщо ξ→η є продукцією граматики G, то кажуть, що α₁ безпосередньо виво­диться зα₀, і записуютьα₀⇒α₁.

Якщо α₀, α₁, …, α_n- ланцюжки над V такі, що

α₀⇒α₁⇒α₂, …, ⇒α_n-1⇒α_{n ,}

то кажуть, щоα₀ породжуєα_n,та використовують записα₁⇒α_n.

Послідовність кроків для отриманняα_п з α₀ називають виведенням.

Приклад 9.2. Речення українською мовою, наведене у прикладі 9.1, може бути виведене у граматиці G=(V,T,S,P),де

V= { , , , , , , , маленька, дівчина, нагодувала, котика},

Т= {маленька, дівчина, нагодувала, котика},

початковий символ , а множина Р містить такі продукції:

→ ,

→ , ,

→ , ,

→маленька,

→ дівчина,

→ нагодувала,

→ котика.

Ця система породжує тільки одне речення, тому їх можна замі­нити на

L= {маленька дівчина нагодувала котика}.

Та якщо ми в цьому випадку захочемо розширити мову, щоб увести до неї речення з означеннями "сусідська", "весела", присудком "попестила", і додатками "цуцика", "кролика" (тоді L матиме 18 речень), то це можна зробити відповідним розширенням алфавіту та додаванням лише п'яти продукцій до множини Р.▲

Приклад 9.3. Розглянемо граматикуG=(V,T,S,P). НехайV={a,b,A,B,S}Т={а,b},S - початковий символ, Р={S→АВа, А→ВВ, В→аb, АВ→b}. ЛанцюжокАаbа безпосередньо виводиться зАВа у цій граматиці, оскільки В-аb є продукцією граматики. Ланцюжок аbаbаbа породжується ланцюжкомАВа, оскільки

АВа⇒Ааbа⇒ВВаbа⇒Ваbаbа⇒аbаbаbа

за допомогою послідовного використання продукцій В→аb,А→ВВ, В→аb таВ→аb.▲

НехайG=(V,T,S,P)- граматика. Мовою, яка породжується G, називають множину всіх ланцюжків терміналів, які виводяться з початкового символу S Мову, що породжується граматикоюGпозначаютьL(G). Отже,

деT- множина всіх ланцюжків терміналів, включно з порожнім ланцюжком.

Приклад 9.4. Нехай G - граматика з алфавітомV={S,А,а,b}, множиною терміналів Т={а,b}, початковим символом S і множи­ною продукцій Р={S→аА,S→b, А→аа}. Знайдемо мову L(G), яка породжується цією граматикою.

Із початкового символу S можна вивести ланцюжокаА, викори­стовуючи продукціюS→aA;або застосувати продукцію щоб вивестиb.ЗаА, скориставшись продукцієюА→аа, можна вивести ланцюжокааа. Ніяких інших ланцюжків вивести не можна. Отже, L(G)={b, ааа}.▲

Приклад 9.5. НехайG-граматика з алфавітом S={S,0,1}, Т={0,1}, початковим символом S та множиною продукцій Р={S→11S, S→0}. Знайдемо L(G).

З S отримаємо 0 (S→0) або 11S (S→11S). З 11S можна отримати 110 або 1111S. З 1111S виводяться 11110 або 111111S. Отже, після кожного виведення ми або додаємо дві одиниці у кінець ланцюжка, або закінчуємо ланцюжок нулем. Тобто L(G)={0, 110, 11110, 1111110, ...} - це множина всіх ланцюжків з парною кількістю тільки 1, після яких (у кінці) обов'язково один 0. ▲

Зауваження. Ми отримали нескінченну мову (L(G) складається з нескінченної кількості ланцюжків). Щоб граматика G породжу­вала нескінченну мову, у множині продукцій повинно бути принайм­ні одне рекурсивне правило (у прикладі 9.5 це правило S→11S).

Важливою є проблема побудови граматики для заданої мови.

Приклад 9.6. Знайдемо граматику, яка породжує мову {0^m1^m| т=0,1,2,...}. Потрібно дві продукції, щоб побудувати ланцюжок, який складається з деякої кількості нулів, за якими є така ж кіль­кість одиниць. Перша продукція нарощує ланцюжок зсередини, додаючи зліва від центру 0, а справа 1. Друга продукція замінює S на порожній ланцюжок λ. Розв'язком є граматика G=(V,T,S,P), V={0,1,S}, T= {0,1}, S - початковий символ, Р={S→0S1,S→𝜆}. ▲

Приклад 9.7. Знайти граматику, яка породжує мову {0^m1ⁿ|m, n=0,1,2,...}.

Таких граматик наведемо дві:

G₁: V={S, 0, 1}, T={0,1}, P={S→0S, S→S1, S→λ};

G2: V={S, A, 0, 1}, T={0,1}, P={S→0S, S→1A,A→1A,A→1A, S→λ}

Пропонуємо обґрунтувати, що обидві ці граматики справді породжують мову {0^m1ⁿ|m, n=0,1,2,...} (див задачі 3, 4). Цей приклад свідчить, що дві різні граматики можуть породжувати одну мову. ▲

Граматики G₁таG₂ називають еквівалентними, якщо L(G₁)=L(G₂). Граматики G₁таG₂з прикладу 9.7 еквівалентні.

Іноді мову, яку легко описати, доводиться задавати достатньо складною граматикою.

Приклад 9.8. Побудуємо граматику, яка породжує мову {0^m1^m2^m|п=0,1,2,...}.

Розв'язком цієї задачі є така граматика:G=(V,T,S,P)V={0,1,2, S,А, В}, Т={0, 1,2}, початковий символ S, множина продукцій

.▲

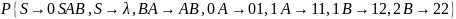Зауваження. Ми отримали нескінченну мову (L(G) складається з нескінченної кількості ланцюжків). Щоб граматика G породжу­вала нескінченну мову, у множині продукцій повинно бути принайм­ні одне рекурсивне правило (у прикладі 9.5 це правило S→11S).

Важливою є проблема побудови граматики для заданої мови.

Приклад 9.6. Знайдемо граматику, яка породжує мову {0^m1^m| т=0,1,2,...}. Потрібно дві продукції, щоб побудувати ланцюжок, який складається з деякої кількості нулів, за якими є така ж кіль­кість одиниць. Перша продукція нарощує ланцюжок зсередини, додаючи зліва від центру 0, а справа 1. Друга продукція замінює S на порожній ланцюжок λ. Розв'язком є граматика G=(V,T,S,P), V={0,1,S}, T= {0,1}, S - початковий символ, Р={S→0S1,S→𝜆}. ▲

Приклад 9.7. Знайти граматику, яка породжує мову {0^m1ⁿ|m, n=0,1,2,...}.

Таких граматик наведемо дві:

G₁: V={S, 0, 1}, T={0,1}, P={S→0S, S→S1, S→λ};

G2: V={S, A, 0, 1}, T={0,1}, P={S→0S, S→1A,A→1A,A→1A, S→λ}

Пропонуємо обґрунтувати, що обидві ці граматики справді породжують мову {0^m1ⁿ|m, n=0,1,2,...} (див задачі 3, 4). Цей приклад свідчить, що дві різні граматики можуть породжувати одну мову. ▲

Граматики G₁таG₂ називають еквівалентними, якщо L(G₁)=L(G₂). Граматики G₁таG₂з прикладу 9.7 еквівалентні.

Іноді мову, яку легко описати, доводиться задавати достатньо складною граматикою.

Приклад 9.8. Побудуємо граматику, яка породжує мову {0^m1^m2^m|п=0,1,2,...}.

Розв'язком цієї задачі є така граматика:G=(V,T,S,P)V={0,1,2, S,А, В}, Т={0, 1,2}, початковий символ S, множина продукцій

.▲