Розділ 7 Основи теорії кодування План викладення матеріалу

7.1. Алфавітне й рівномірне кодування.

7.2. Дотатні умови однозначності декодування. Властивості розділових кодів.

7.3. Оптимальне кодування.

4. Коди, стійкі до перешкод. Коди Хемінга.

Задачі.

Комп 'ютерні проекти.

Література.

7.1. Алфавітне й рівномірне кодування

Кодування - у широкому розумінні - це перехід від одного спо­собу задання інформації до іншого, який дає змогу відновлювати початкову інформацію. Теорія кодування виникла в 40-х роках XX століття після робіт К. Шеннона (С. Shannon). У цій теорії дослід­жуються методи кодування, пов'язані з основними математичними моделями, які відображають істотні риси реальних інформаційних систем.

Не зменшуючи загальності, задачу кодування можна сформулю­вати так. Нехай заданий алфавіт А={а₁,... ,а_r}, який складається зі скінченної кількості букв. Скінченну послідовність символів алфа­віту А: α = α_i1 α_i2 …α_il називають словам в алфавіті А,а число l - дов­жиною слова α. Довжину слова α позначаютьl(α).Множину всіх слів в алфавіті А позначають черезA*. 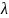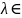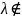Порожнє слово не містить жодної букви, його позначають , A*, l( )=0, A.

Якщо 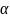= _{1 2}, то ₁ називають початком,або префіксом слова , а ₁ – закінченням, або постфіксом слова .Якщо при цьому ₁≠λ(відповідно, ₂≠λ), то α₁(відповідно, α₂) називають власним початком (відповідно, власним значенням) слова α.

Нехай S – деяка підмножина множини A*, елементимножиниSназиваютьповідомленнями. Нехай також задано скінченнийB ={b₁,…,b_q}.Через β позначмо слово в алфавітіBі через B* -- множинувсіхсліввалфавітіB. ЗадамовідображенняF, яке кожному слову α, α S, ставить у відповідність слово β=F(α),β B*. Слово βназивають кодом повідомленняα. Перехід від слова α до його коду називають кодуванням.

Якщо ƖBƖ =q, то кодування називають q-кодовим. Найбільш поширений випадок B={0,1}– двійкове кодування. Саме цей випадок й розглядатимемо в подальшому, слово "двійкове" випускатимемо.

Відображення Fзадаютьдеяким алгоритмом. Розглянемодва способи задання відображення F.

Алфавітне кодування.Алфавітне кодування задають схемою (або таблицею кодів) σ:

α₁→β₁,

α₂→β₂,

………..

α_r→β_r,

де α₁ϵА, β₁ B*, i=1,…,r. Схема σ задає відповідність між буквами алфавіту A і деякими словами алфавіту B. Вона визначає алфавітне кодування так: кожному слову = α_i1α_i2 … α_il з S ставиться у відповідність слово β = β_i1 β_i2 … β_il. Це слово β називають кодом слова . Слова β₁,…, β_r (див. схему σ) називаютьелементарними кодами.

Рівномірнекодування. Рівномірнекодування зпараметрами k та n визнaчають так. Повідомлення α розбивають на блоки довжини k:

,

Де s≤k (останній блок може бути коротшим, у такому разіспосібйогокодуванняспеціальнообумовлюється), x_i A, i=1, …,mk+s. Блоки довжини kрозглядають як буквидеякогоалфавіту (таких блоків є, очевидно, r^k, оскількиалфавітА складається з r букв ) і кодують словами в алфавіті Bоднаковоїдовжиниn за схемою рівномірного кодування σ_k,n:

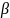₁→ ₁

₂→ ₂

₃→ ₃

………

Надлишковістю схеми σ_k,n на символ повідомленняназивають величину

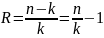
Отже, ми описали два способи задання відображення F: S→B*. Однозначне декодування є можливим, якщо існує обернене відображення F^-1.