9.5. Форми Бекуса-Наура

Для граматик типу 2 (контекстно вільних), окрім звичайного, є ще інший спосіб подання - форми Бекуса-Наура.

Продукції граматик типу 2 мають у лівій частині один символ (нетермінальний). Замість того, щоб виписувати окремо всі продук­ції, можна об'єднати в один вираз продукції з однаковими симво­лами у лівій частині. У такому разі замість символу →у продукціях використовують символ ::=. Усі нетермінали в цьому випадку беруть у трикутні дужки . Праві частини продукцій в одному виразі відокремлюють одну від одної символом |.

Приклад 9.16. Три продукціїА→Аа, А→а та А→АВ можна зобразити таким одним виразом у формі Бекуса-Наура:

.▲

Приклад 9.17. Знайдемо продукції граматики, якщо у формі Бекуса-Наура вони записані так:

.

Р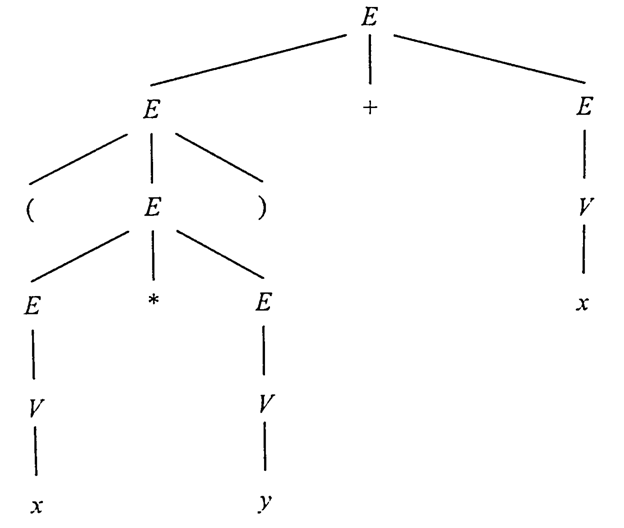 ис. 9.5

Зобразимо дерево виведення у цій граматиці для ланцюжка (х*у)+х.

Для зручності використаємо позначення Е для (це буде й початковий символ) та Vдля .Тоді правилами пере­творення (продукціями граматики) будуть E→(E), Е→Е+Е, E→E*EтаE→Vз першого виразу, а такожV→х таV→у з другого виразу. Дерево виведення для ланцюжка (x*y)+xзображено на рис. 9.5.▲

9.6. Скінченні автомати з виходом

Скінченні автомати і такі тісно пов'язані з ними конструкції, як, наприклад, регулярні граматики та регулярні вирази, належать до найважливіших понять інформатики. Різні варіанти скінченних автоматів використовують для опису й аналізу технічних пристроїв, різних систем і процесів, програм і алгоритмів. На ґрунті теорії скінченних автоматів сформовано багато складних концепцій теоретичної інформатики. Теорія скінченних автоматів має чимало застосувань у технічній інформатиці і є важливою частиною теоретичної інформатики.

Розглядатимемо скінченні автомати як абстрактні моделі най­простіших пристроїв опрацювання даних. Спосіб викладення орієнтований, передусім, на теорію формальних мов.

Скінченним автоматом називають системуM=(S, I, O,f, g, s₀), у якійS, І, О - скінченні множини, af:S×I→Sтаg: S×I→O- функції, визначені на декартовому добуткуS×l.МножинуSназивають множиною станів, І- вхідним алфавітом, О-вихідним алфавітом,f- функцією переходів, g-функцією виходів, виділений елементs₀∈S- початковим станом.

Елементи вхідного алфавіту називають вхідними символами (входами), а вихідного - вихідними символами (виходами).

Рівністьf(s_i, x)=s.означає, що у разі входу х автомат, який перебуває в станіs_i,переходить у стан s_j,а рівністьg(s_i,х)=y, - щов цьому разі на виході з'являєтьсяy; тутssss_i,s_j∈S, х∈I, y∈О.

Оскільки функціїfтаgвизначені на скінченних множинах, то їх можна задавати таблицями. Звичайно дві таблиці зводять в одну і називають таблицею станів, або автоматною таблицею. Цятаблиця містить значення функції переходів f та функції виходів g для всіх пар (s, х), деs∈S, х ∈I.

Таблиця 9.2

Стан	F	G
	Вхід	Вхід
	0 1	0	1
s0 s1 s2 s3	s1s0 s3s0 s1s2 s2s1	1 0 1 1 0 1 0 0

Приклад 9.18. Табл. 9.2 задає функції переходів і виходів для автомата з множиною станівS={s₀, s₁, s₂, s₃}та вхідним і вихіднималфавітамиI={0,1}, O={0,1}.▲

Ще один поширений і наочний спосіб задання автоматам орієнтований мультиграф, який називають діаграмою станів. Вершини графа відповідають станам; якщоf(s_i, x_j)=s_kта g(s_i, x_j)=y_r, та то із вершини s_i. у вершину s_k веде дуга, на якій записані через кому х_j та y_r. Тут x_j∈I,y_r∈О. Кратні дуги не обов'язкові; якщо є дві кратні дуги, то їх можна замінити однією, на якій написати обидві пари вхідний символ-вихідний символ.

Приклад 9.19. Діаграму станів для автомата, заданого табл. 9.2, зображено на рис. 9.6. ▲

Рис. 9.6

Для заданого скінченного автомата М його функція виходів g може бути визначена не тільки на множині I всіх вхідних символів (букв), а й на множині I* всіх вхідних ланцюжків (слів). Нехай вхідний ланцюжокα=x₁x₂…х_k. Тоді під час читання цього ланцюжкаавтомат спочатку переходить зі стануs₀ у станs₁ деs₁=f(s₀, x₁)після цього у станs₂ деs₂=f(s₁, x₂), і цей процес триває до досягнен­ня стануs_k=f(s_k-1, x_k). Звернемо увагу, що тут x_k-останній символ вхід­ного ланцюжка. Ця послідовність переходів у нові стани формує вихід­ний ланцюжок ω=y₁y₂…y_kде y₁=g(s₀, x₁) вихідним символом, який відповідає переходузs₁ в s₂,y₂=g(s₁, x₂) - вихідним символом, який відпо­відає переходу зs₁ в s₂і цей процес триває до отримання вихідного символу y_k=g(s_k-1, x_k). У загальномуy_j=g(s_j-1, x_j)дляj=1, 2,.., k.. Отже, ми можемо розширити означення функції виходів на вхідні ланцюжки так, щоg(α)=ω, де вихідний ланцюжок со відповідає вхідному ланцюжку α.

Приклад 9.20. Знайдемо вихідний ланцюжок, який видасть скінченний автомат з рис. 9.6, якщо вхідний ланцюжок 101001.

Автомат на виході видасть ланцюжок 011110. Послідовність станів і вихідних символів наведено у табл. 9.3. ▲

Таблиця 9.3

Вхід	101001 -
Стан Вихід	s0s0 s1 s0 s1 s3 s1 0 1 1 1 1 0 -

Нехай М- скінченний автомат. Кожному вхідному ланцюжку α поставимо описаним вище способом у відповідність вихідний ланцюжок ω. Цю відповідність, яка відображає вхідні ланцюжки у вихідні ланцюжки, називаютьавтоматним відображенням, а такожавтоматним (абообмежено детермінованим) оператором,який реалізується автоматом М.Іноді говорять коротко - операторМ; якщо результатом застосування цього оператора до ланцюжка α є вихідний ланцюжок ω, то це позначають М(α)=ω. Кількість символів у ланцюжку α, як завжди, називають довжиною α і позначають |α| або l(α).

Автоматне відображення має дві властивості: 1) ланцюжки α та ω=М(α)мають однакову довжину: |α|=|ω| (властивість збере­ження довжини); 2) якщо α =α ₁α₂ і M(α₁ α₂)=ω₁ω₂ де |α₁|=|ω₁|, то М(α₁)=ω₁, тобто образ відрізка довжини l дорівнює відрізку образу такої ж довжини. Властивість 2 відображає той факт, що автоматні оператори - це оператори без випередження, тобто оператори, які, переробляючи ланцюжок зліва направо, "не підглядають вперед": i-та буква вихідного ланцюжка залежить тільки від перших і букв вхідного ланцюжка. Приклад оператора з випередженням - опе­ратор, який ланцюжку α=х₁х₂..х_k ставить у відповідність ланцюжок х_k…х₂х₁; перша буква вихідного ланцюжка тут дорівнює останній букві вхідного ланцюжка. Зазначимо, що ці дві властивості не є достатніми умовами автоматності відображення: існують відобра­ження, які задовольняють умови 1та 2, але не реалізуються в скінченному автоматі.

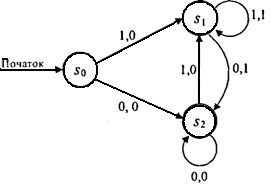
Рис. 9.7

Розглянемо деякі корисні приклади скінченних автоматів. Ці приклади свідчать, що стани скінченного автомата дають змогу використовувати їх як скінченну пам'ять. Стани можна вико­ристовувати для запам'ятовування ситуацій або символів, якіподаються на вхід. Та оскільки є лише скінченна множина станів, то скінченні автомати не можуть бути використані у деяких важливих призначеннях.

Приклад 9.21. Важливим елементом у багатьох пристроях є авто­мат одиничної затримки. Він видає на виході вхідний ланцюжок, затриманий на одиницю часу. Отже, якщо на вхід подано двійковий ланцюжокx₁x₂..x_k, то на виході буде ланцюжок0x₁x₂..x_k-1

Такий автомат повинен мати два вхідні символи (нехай це будуть 0 та 1), початковий станs₀ і пам'ятати, який з двох символів 0 або 1 був на вході у попередній момент. Отже, потрібно ще два стани: нехай автомат буде в стані s₁, якщо попереднім вхідним символом була 1, і в стані s₂, - якщо 0. На виході за початкового стану завжди буде 0 незалежно від входу. Кожний перехід зі стану s₁дає на виході 1, а зі стану s₂- 0. Діаграма станів цього автомата зображена на рис. 9.7. ▲

Приклад 9.22. Побудуємо скінченний автомат для додавання двох цілих додатних чисел у двійковій системі.

Нехай додаємо числа(х_п…х₁х₀)₂ та(у_п…y₁y₀)₂. Спочатку додаємо розряди х₀ та у₀, у результаті отримуємо розряд сумиz₀ та біт пере­несення с₀. Цей біт дорівнює 0 або 1. Далі розряди х₁ та у₁ додаємо разом з бітом перенесення c₀. Це дає розряд суми z₁ і біт перене­сення с₁. Процедуру продовжуємо до стадії підсумовування розря­дівx_n, y_nта попереднього біта перенесенняс_п-1;отримаємо розряд сумиz_п і біт перенесенняс_п, який дорівнює розряду сумиz_п+1.

Таблиця 9.4

Стан	F				g
	Вхід				Вихід
	00	01	10	11		00	01	10	11
s0	s0	s0	s0	s1		0	1	1	0
s1	s0	s1	s1	s1		1	0	0	1

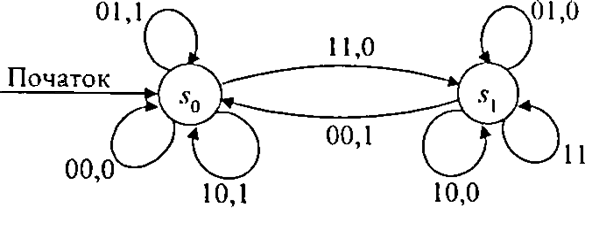Рис. 9.8

Вхідний алфавіт автомата складається з чотирьох символів: I={00,01,10,11}. Це необхідно для зображення можливих значень х_i та у_i - значень i-го розряду обох доданків. Вихідний алфавіт: O={0,1}. Множина станівS={s₀,s₁}. Станs₀відповідає відсутності 1 перенесення з попереднього розряду, цей же стан початковий. Стан Sjвідповідає наявності 1 перенесення з попереднього роз­ряду. Розв'язок наведено у вигляді таблиці станів (табл. 9.4) і діаграми станів (рис. 9.8). ▲

Приклад 9.23. Побудуємо скінченний автомат, який видає на виході 1 тоді й лише тоді, коли на вході останніми трьома симво­лами були 1.

Цей автомат повинен мати три стани. Початковий станs₀, цей же стан використовують для запам'ятовування випадку, коли попе­редній вхідний символ 0. Стан s₁відповідає випадку, коли попе­редній символ на вході 1, але символ перед ним - 0. Станs₂запам'ятовує випадок двох поспіль вхідних 1. Отже, якщо автомат перейшов зі стануs₁у станs₂,то на вхід подано дві 1 поспіль. Вхід 1 у стані s₂ означає, що це була третя поспіль 1, і на виході видається 1. У всіх інших випадках на виході видається 0. Діаграма станів цього автомата зображена на рис. 9.9. ▲

Автомат з прикладу 9.23 подає мову, оскільки він видає на виході 1 тоді й лише тоді, коли вхідний ланцюжок (слово) має спеціальні властивості (в цьому прикладі мова складається з ланцюжків нулів та одиниць, які закінчуються трьома 1 поспіль).

Подання мов є одним з найважливіших застосувань скінченних автоматів.

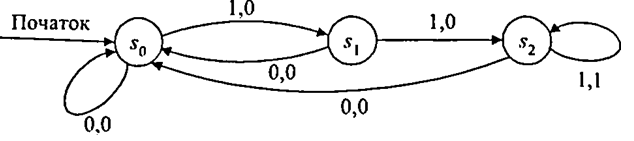
Рис. 9.9

Автомати, які ми розглянули, називають автоматами Мілі (G. Mealy).Вперше їх уведено 1955 р. Є також інший тип авто­матів з виходом, так звані автомати Мура (Е. Moore), запроваджені 1956 р. У цих автоматах вихід визначається лише станом, тобто не залежить від вхідного сигналу.

У прикладі 9.23 описано, як автомат Мілі можна використати для задання мови. Проте з цією метою звичайно застосовують інший тип автоматів - скінченні автомати без виходу. Такі автомати мають множину заключних (або приймаючих) станів і допускають ланцю­жок тоді й лише тоді, коли цей ланцюжок переводить автомат без виходу із початкового стану у заключний стан.