7.2. Достатні умови однозначності декодування. Властивості роздільних кодів

Розглянемо схему алфавітного кодування σ і різні слова, складені з елементарних кодів. Схему σ називають роздільною, якщо з рівності

випливає, що k=lта i_t=j_tдля кожного t=1,…,k,тобто будь-яке слово, складене з елементарних кодів, єдиним способом розкладається на елементарні коди. Очевидно, що алфавітне кодування з розділь­ною схемою допускає однозначне декодування.

Схему σ називають пефіксною, якщо для будь яких i та j (I, j=1,…,r,i≠j) елементарний код _iне є префіксом елементарного коду _j.

Теорема 7.1.Префіксна схема є роздільною.

Доведення. Від протилежного. Оскільки схема σ є префіксною, то всі елементарні коди в σ попарно різні, тобто _i ≠ _j , якщо i≠j. Нехай кодування зі схемою σ не є роздільним. Тоді існує слово ∈B*, яке допускає два розклади на елементарні коди

= _i1… _ik , = _j1… _jl.

Нехай _­ , але 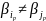.Утакому разі одне із слів _i1 , _j1 є префіксаміншого, а цесуперечить тому,що схема префіксна. ▲

Властивість префікеності є достатньою, але не є необхідною умо­вою роздільності схеми.

Приклад 7.1. Нехай А={а,b}, B= {0,1}, схема σ: а→0, b→01. Ця схема не префіксна, але роздільна. Справді, перед кожним вход­женням 1 у слові ₂, безпосередньо є 0. Це дає змогу виділити всі пари (01). Частина слова, що залишиться, складатиметься із сим­волів 0. ▲

Нехай - слово з В*. Позначимо через ^͠βслово, яке одержують оберненням слова , тобто 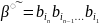.Позначимо ͠σ схему вигляду

α₁→ ^͠β₁

α₂→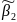

…

α_r→ ^͠β_r.

Приклад 7.2. Візьмемо схему σ із прикладу 7.1. Тоді ͠σ вигляда­тиме так: а→0, b→10. Тут схема ͠σ є префіксною і за теоремою 7.1 - роздільною. ▲

Зауваження. Схеми σ та ͠σ обидві або є роздільними, або ні. ▲

Це зауваження дає змогу посилити теорему 7.1.

Теорема 7.2. Якщо або схема σ, або схема ͠σ є префіксною, то обидві схеми σ та ͠σ є роздільними. ▲

Можна навести приклад роздільної схеми σ такої, що ні σ, ні ͠σ не є префіксними. Отже, теорема 7.2 також дає достатню, але не необхідну умову роздільності схеми.

Для того, щоб схема алфавітного кодування була роздільною, необхідно, щоб довжини елементарних кодів задовольняли нерів­ність Макміллана (В. McMillan).

Теорема 7.3 (нерівність Макміллана). Якщо схема алфавітного кодування σ роздільна, то

Доведення. Позначимо L=mах{l₁, l₂,..., l_r}. Запишемо n-й степінь лівої частини нерівності

Розкривши дужки, отримаємо суму

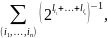
де (i_1,..., і_n)- різні набори номерів елементарних кодів. Позначимо як v(n, m) кількість доданків вигляду 1/2^m, які входять у цю суму; тут 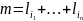. Для деяких m може бути v(n, m)=0. Зведемо подібні члени й отримаємо суму

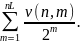
Кожному доданку вигляду можна однозначно зіста­вити код (слово в алфавіті В) вигляду . Це слово складається з n елементарних кодів і має довжинуm. Отже, v(n,m) - це кількість деяких слів вигляду таких, що . Оскільки схема σ роздільна, то v(n,m) ≤2^т. Справді, якщо припустити v(n, m)>2^m, то за принципом коробок Діріхле існує два однакових слова ,які допускають різний розклад. Можемо записати

Отже, для кожного n виконується нерівність

тобто звідки

▲

Зауваження. У теоремі 7.3 розглянуто нерівність Макміллана для двійкового кодування. Для загального випадку q-кового коду­вання вона виглядає так:

▲

Розглянемо ще один важливий факт.

Теорема 7.4. Якщо числа l₁,…,l_nзадовольняють нерівність

то існує префіксна схема алфавітного кодування σ:

α₁→β₁

…

α_r→β_r

де l₁=l(β₁),…, l_r=l(β_r)

Доведення. Без зменшення загальності можна вважати, що l₁≤l₂≤…≤l_r. Розіб'ємо множину чисел {l₁,...,l_r} на класи еквіва­лентності так:li та l_j належать одному класу тоді й лише тоді, коли l_i=l_j. Нехай μ (1≤μ≤r) - кількість класів, а λ₁,…, λ_μ таv₁,...,v_μ позна­чають, відповідно, представників та потужності класів. Можна також уважати, що λ₁< λ ₂<…< λ_μ .

Тоді нерівність Макміллана можна переписати у вигляді

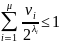
Ця нерівність породжує серію допоміжних нерівностей:

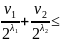1, звідки ;

……………………………………………………………

Розглянемо слова довжини λ₁, у двійковому алфавіті В. Оскіль­ки , то можемо вибрати з них v₁різних слів β₁,..., β_v1 довжини λ₁. Виключимо з подальшого розгляду всі слова з В*, які почина­ються зі слів β₁,..., β_v1. Далі розглянемо множину слів в алфавіті В, які мають довжину λ₂ і не починаються зі слів β₁,..., β_v1. Таких слів, очевидно, є . Оскільки , то із цієї множини можна вибрати v₂різних слів. Позначимо їх через . Виключимо слова з В*, які починаються з , з подальшого розгляду. Продовжимо цей процес, вико­ристовуючи поступово допоміжні нерівності. 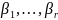У результаті побудуємо слова , де

Якщо взяти ці слова як елемен­тарні коди, то отримаємо деяку схему алфавітного кодування σ. Ця схема, очевидно, є префіксною. Крім того, l(β₁)=l₁,…,l(β_r)=l_r. ▲

Наслідок 1. Нерівність Макміллана є необхідною й достатньою умовою існування алфавітного кодування із префіксною схемою й довжинами елементарних кодів, що дорівнюють l₁,..., l_r. ▲

Наслідок 2. Якщо існує роздільна схема алфавітного кодування із заданими довжинами елементарних кодів, то існує також і пре­фікс на схема з тими самими довжинами елементарних кодів.

Для доведення потрібно спочатку застосувати теорему 7.3, а потім - теорему 7.4. ▲