8.3. Спеціальні форми зображення булевих функцій в алгебрах Буля і Жегалкіна

Спеціальними формами зображення булевих функцій в алгебрі Буля є диз'юнктивні нормальні форми та кон'юнктивні нормальні форми, а в алгебрі Жегалкіна - поліном Жегалкіна.

8.3.1. Диз'юнктивні нормальні форми

Уведемо позначення , де σ - параметр, який дорів­нює 0 або 1. Очевидно, що

Зазначимо, що σ^σ=1 .

Зафіксуємо множину змінних Х={х₁,х₂, ..., х_п}.

Елементарною кон'юнкцією називають формулу , де х_ij змінні з множиниX, причому всі х_ij різні. Числоr називають рангом кон'юнкції. У випадкуr= 0 кон'юнкцію називають порожньою і вважають такою, що дорівнює 1.

Приклад 8.10. Елементарними кон'юнкціями є 1, а формули 0, х₁х₂х₁, ,елементарними кон'юнкці­ями не є. ▲

Елементарну кон'юнкцію, яка містить усі змінні з множини X, називають конституентою одиниці. Іншими словами, конституента одиниці -- це елементарна кон'юнкція рангу п. Легко побачити, що всіх різних конституент одиниці для фіксованої множини п змінних x₁,x₂, …, x_nє стільки, скільки є двійкових наборів з п компонентами, тобто 2^п.

Диз'юнктивною нормальною формою (ДНФ) називають диз'юнкцію елементарних кон'юнкцій k_j ,у якійk_j(j=1,2, …, 5) попарно різні.

Існує алгоритм, який дає можливість для будь-якої формули булевої алгебри тотожними перетвореннями знайти рівносильну їй ДНФ.

На першому етапі цього алгоритму формулу перетворюють у рівносильну, побудовану зі змінних та їхніх заперечень за допомогоюсамих лише кон'юнкцій та диз'юнкцій (тобто заперечення можуть бути лише над змінними). Для цього використовують закони де Моргана та закон подвійного заперечення.

На другому етапі досягають, щоб усі кон'юнкції виконувались раніше диз'юнкцій, для чого розкривають дужки на основі дистри­бутивного закону для кон'юнкції відносно диз'юнкції. Далі на основі співвідношень для констант і закону протиріччя виключають нулі й на основі законів ідемпотентності об'єднують рівні члени. На цьому процес побудови ДНФ закінчують.

Приклад 8.11.Зведемо до диз'юнктивної нор­мальноїформи. Використовуючи сформульований алгоритм,

можемо записати

. ▲

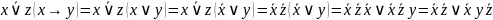ДНФ булевої функції не єдина, наприклад,

Досконалою диз'юнктивною нормальною формою (ДДНФ) нази­вають ДНФ, у якої кожна елементарна кон'юнкції є конституентою одиниці.

Теорема 8.3.Будь-яку булеву функціюf(х₁,..., х_n)≠0 можна єдиним способом зобразити в досконалій диз'юнктивній нормаль­ній формі.

Доведення. Нехай задано деяку функціюf(x₁,..., x_n)≠0. Кожному двійковому наборуа_п=(а₁,а₂,...,а_п) значень змінних відповідає єдина конституента одиниці, яка перетворюється на цьому наборі в 1 і визначена так: . Усі інші конституента одини­ці на даному наборі перетворюються в 0. Наприклад, набору 0101 відповідає конституента .

Нехайf_i- значення функції, яке вона приймає на i-му двійковому наборі (і=0,1, ..., 2ⁿ-1), К_i- конституента одиниці, що відповідає i-му набору Доведемо рівність

Для l-го наборуf_l =0 . Нульові члени вдиз'юнкції можна випустити. Отже, диз'юнкція конституентодиниці, що відповідають усім двійковим наборам, на якихбулевафункція приймає значення 1, є ДДНФ функції:

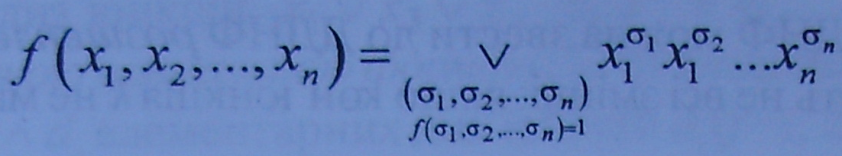
Для доведення єдиності ДДНФ скористаємось таким комбінатор­ним міркуванням. Знайдемо кількість ДДНФ від n змінних x₁, ..., х_n. Для цього будь-яким способом занумеруємо конституента одиниці, їх є 2ⁿ. Кожній ДДНФ від змінних x₁, ...,х_n можна таким взаємно однозначним способом поставити у відповідність набір із 2ⁿнулів і одиниць. Компоненти з номерами конституент одиниці, які входять у ДДНФ, дорівнюють одиниці, а решта компонент - нулю. Нульовий набір при цьому не отримаємо, тому що він відповідав би порожній ДДНФ. Отже, різних ДДНФ буде стільки, скільки існує наборів довжини 2ⁿ, відмінних від набору із самих лише нулів, тобто . Функцій (за виключенням тотожного нуля) відзміннихx₁,..., x_птакож є . Кожну із цих функцій можна зобразити ДДНФ, отже, це зображення єдине. ▲

Із доведення теореми 8.3 випливає, що для заданої таблично функції ДДНФ будують так: для кожного набору, на якому функція приймає значення 1, будують відповідну цьому набору констшуенту одиниці; диз'юнкція всіх цих конституент і є ДДНФ заданої функції.

Приклад 8.12.Побудуємо ДДНФ для функції, заданої табл. 8.5.

Таблиця 8.5

x1x2	f(x1,x2)
0 0 0 1 1 0 1 1	1 0 0 1

Функція приймає значення 1 на наборах 00 та 11. Отже,

Будь-яку ДНФ можна звести до ДДНФрозщепленнямкон'юнкцій, які містять не всі змінні: якщо кон'юнкціяk не містить змінної х, то

Приклад 8.13.Перетворимо диз'юнктивну нормальну форму у досконалу. Застосовуючи розщеплення для кон'юнкції і закон ідемпотентності для диз'юнкції, одержимо

.▲

Якщо із формули F₁, деякими тотожними перетвореннями можна отримати формулу F₂, то F₁можна отримати із F₂, використову­ючи ті самі тотожні перетворення. Іншими словами, будь-яке тотожне перетворення можна обернути.

Теорема 8.4.Для довільних рівносильних формул алгебри Буля F₁та F₂існує еквівалентне перетворення F₁ вF₂ за допомогою основних законів цієї алгебри.

Доведення.ПеретворимоF₁та F₂у ДДНФ. Оскільки F₁та F₂рівносильні, то їхні ДДНФ збігаються. Обертаючи друге перетво­рення, отримаємо такий ланцюжок перетворень:F₁⇒ДДНФ⇒F₂. ▲

Важливість цієї теореми в тому, що основних законів алгебри Буля виявляється достатнім для довільних еквівалентних перетво­рень у цій алгебрі.