8.2. Алгебри булевих функцій

Нехай функція задана формулою F₁ а функція ƒ₂ - формулою F_2. Підстановка F₁та наприклад, у диз'юнкцію x₁˅x₂ дає формулу F₁˅F₂. Якщо взяти формулу Ф1, рівносильну F₁ (тобто Ф₁ також реалізує ) і , рівносильну , то отримаємо формулу Ф₁∨Ф₂, рівносильну F₁∨F₂.

Отже, диз'юнкцію можна розглядати як двомісну операцію на множині всіх булевих функцій. Ця операція кожній парі функцій f₁та f₂, незалежно від вигляду формул, якими ці функції зображені, однозначно ставить у відповідність функцію f₁∨f₂. Аналогічно й інші булеві функції можна розглядати як операції на множині Р₂ усіх булевих функцій. Наприклад, заперечення є одномісною операці­єю, кон'юнкція та диз'юнкція - двомісними.

Множину Р₂ булевих функцій разом із уведеною на ній системою операцій називають алгеброю булевих функцій.

Розглянемо дві алгебри. Алгебру (Р₂; ̅ , ∧, ∨), операціями якої є заперечення, кон'юнкція та диз'юнкція, називають алгеброю Буля.

Алгебру (Р₂;∧, ⊕), операціями якої є кон'юнкція й додавання за mod2, називають алгеброю Жегалкіна.

Формули алгебри Буля та алгебри Жегалкіна будують із знаків операцій відповідної алгебри, круглих дужок, символів змінних і констант 0 та 1.

Порядок виконання операцій у разі відсутності дужок у булевій алгебрі такий: заперечення, кон'юнкція, диз'юнкція. В алгебрі Жегалкіна спочатку виконують кон'юнкцію, а потім - додавання за mod2. У разі наявності дужок спочатку повинні виконувати опе­рації всередині них. У булевій алгебрі роль дужок у разі заперечення складних виразів відіграє сам символ заперечення.

Приклад 8.5. Замість можна написати , а замість (xy)⊕(yz) записуютьxy⊕yz. ▲

Однією з найважливіших задач є виявлення основних еквіваленгностей, які є в алгебрах, що розглядаються. Ці еквівалентності називають законами відповідної алгебри.

Закони алгебри Буля.

Закони асоціативності

Закони комутативності

Дистрибутивний закон для кон’юнкції відносно диз’юнкції

Дистрибутивний закон для диз'юнкції відносно кон’юнкції

Закон подвійного заперечення

Закони де Моргана

Закони ідемпотентності

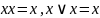
Закони поглинання

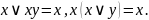
Співвідношення для констант

Закон виключеного третього

Закон протиріччя

Закони алгебри Жегалкіна.

Закони асоціативності

Закони комутативності

Дистрибутивний закон для кон’юнкції відносно додавання за mod2

Співвідношення для констант

.

Закон ідемпотентності для кон’юнкції

.

Закон зведення подібних членів у разі додавання за тоді

Правильність цих еквівалентностей доводять за допомогою таблиць.

Наведені еквівалентності залишаються правильними й у разі підстановки замість змінних довільних булевих функцій (тобто фор­мул, які ці функції задають). Важливо лише виконувати таке правило підстановки формули замість змінної: під час підстановки формули F замість змінної х усі входження змінної х у дану еквівалентність повинні бути одночасно замінені формулою F. Наприклад, з отримаємо .

Закони алгебр Буля та Жегалкіна дають змогу доводити нові еквівалентності вже без таблиць, на основі тотожних перетворень.

Приклад 8.6. Доведемо, що

а) ;

б) .

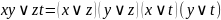Двічі використовуючи закони дистрибутивності, одержимо:

а) ;

б) .▲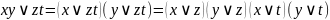

Приклад 8.7. Доведемо, що . Використову­ючи закони де Моргана, подвійного заперечення та асоціативності, можемо записати

. ▲

Наведемо еквівалентності, які дозволяють перетворити будь-яку формулу булевої алгебри у рівносильну їй формулу алгебри Жегалкіна та навпаки:

Зазначимо, що за допомогою законів алгебр Буля та Жегалкіна можна спрощувати різні формули в цих алгебрах.

Приклад 8.8. Перетворимо у рівносильну формулу алгебри Жегалкіна. Отриману формулу спростимо.

.▲

Виразимо х→у тах~у через операції алгебри Буля. Оскільки х~у=(х→у)(у→х), то достатньо виразитих→у. Порівняємо таблицю для х→у з таблицею для x∨y. Скориставшись тим, що в обох таблицях є єдиний набір, для якого значення функції дорівнює нулю, отримаємо еквівалентність .

Розглянемо тепер ще одне важливе поняття. Функціюf^*(х₁,..., x_n) називають двоїстою до функції f(х₁,..., x_n), якщо . Візьмемо заперечення над обома части­нами рівності і підставимо замість . Отримаємо , тобто функція f двоїста до f*: (f)*⁼f. Отже, відношення двоїстості між функціями симетричне. Пару двоїстих функцій складають, наприклад, кон'юнкція та диз'юнкція. Таблицю для двоїстої функції у разі вибраного порядку наборів отримують із таблиці для функції інвертуванням (тобто заміною 0 на 1 і 1 на 0) стовпчика функції і перевертанням цього стовпчика.

Розглянемо тепер ще одне важливе поняття. Функціюf^*(х₁,..., x_n) називають двоїстою до функції f(х₁,..., x_n), якщо . Візьмемо заперечення над обома части­нами рівності і підставимо замість . Отримаємо , тобто функція f двоїста до f*: (f)*⁼f. Отже, відношення двоїстості між функціями симетричне. Пару двоїстих функцій складають, наприклад, кон'юнкція та диз'юнкція. Таблицю для двоїстої функції у разі вибраного порядку наборів отримуєть із таблиці для функції інвертуванням (тобто заміною 0 на 1 і 1 на 0) стовпчика функції і перевертанням цього стовпчика.

Із означення двоїстості зрозуміло, що для довільної функції дво­їсту функцію визначають однозначно. Зокрема, може з'ясуватись, що функція є двоїстою до самої себе. У цьому випадку її називають самодвоїстою. Наприклад, заперечення та функціяx⊕y⊕z- самодвоїсті функції.

Нехай функція задана формулою F. Який вигляд має формула F*, яка виражає двоїсту функцію? Відповідь на це запитання дає наступ­на теорема.

Теорема 8.2. Якщо

то

Доведення.

.▲

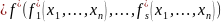З теореми випливає таке твердження.

Принцип двоїстості. Якщо у формулі F яка реалізує функцію f, усі символи функцій замінити, відповідно, на символи двоїстих функцій, то отримана формула F^* реалізує функцію f*, двоїсту до f.

В алгебрі Буля принцип двоїстості має простіший вигляд.

Принцип двоїстості в алгебрі Буля. Якщо у формулі F, яка реалізує функцію f, усі кон'юнкції замінити на диз'юнкції, диз'юнк­ції - на кон'юнкції, 1 замінити на 0, 0 - на 1, то отримана формула F* реалізує функцію f^* ,двоїсту до f.

Приклад 8.9. Знайдемо функцію, двоїсту до

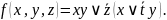
За принципом двоїстості матимемо

Зазначимо, що у разі використання принципу двоїстості потрібно враховувати пріоритет операцій, отже, у разі потреби розставляти дужки. Так, у формулі спочатку виконували кон'юнкціїху та ; отже, у формулі, яка реалізує двоїсту функцію, спочатку треба виконувати диз'юнкції х у та , для чого потрібно ввести дужки. ▲

Якщо функції рівні, то і двоїсті їм функції також рівні. Це дає змогу за допомогою принципу двоїстості отримати нові еквівалентності. Для цього потрібно від еквівалентності F₁=F₂ за допомогою вказаних замін перейти до еквівалентності .