3.3Статистичні міри інформації

3.3.1Відповідність між ймовірністю і інформацією

Очевидно, що, принаймні з точки зору одержувача інформації, повідомлення є випадковими подіями. Тому при імовірнісному підході інформація розглядається як повідомлення про результат випадкових подій, реалізації випадкових величі і функцій, а кількість інформації ставиться в залежність від апріорної ймовірності цих подій, величин, функцій.

Коли надходить повідомлення про події, що часто зустрічаються, ймовірність появи яких прямує до одиниці, тобто до показника повної достовірності, то таке повідомлення є мало інформативним. Настільки ж мало інформативні повідомлення про протилежні події (анти події), ймовірність яких прагне до нуля і які, тому, майже неможливі. Наприклад, подія «годинник йде» має ймовірність , тоді як анти подія «годинник не йде» має ймовірність .

Подія і антиподія складають одну двійкову однопредметну подію. Може бути також двійкова двохпредметна подія, що полягає у виборі одного з двох можливих предметів, наприклад, чорної або білої кулі з урни, герба або решки на монеті.

Більшість видів інформації можна звести до двійкових явищ «так – ні» і до пари: «подія — анти подія». Саме ця пара явищ є простим і неподільним елементом (квантом) інформації.

Інший вид повідомлень складають двохпредметні двійкові явища, які розпадаються на чотири елементарні акти. Наприклад: 1) вийнята біла куля; 2) не вийнята біла куля; 3) не вийнята чорна куля; 4) вийнята чорна куля.

Можуть бути також події, що виключають одна одну. Наприклад, якщо випав герб, то не може одночасно випасти решка, якщо в ланцюзі встановилася напруга 100 в, то не може в тому ж ланцюзі одночасно існувати напруга 12 в.

Будемо під подією далі розуміти елементарне однопредметне явище, яке може відбутися з ймовірністю від до або не відбутися з ймовірністю від до .

Коли і , то матиме місце найбільша невизначеність в ситуації.

Події можна розглядувати як можливі результати деякого досліду, причому всі результати складають ансамбль, або повну групу подій. Остання характеризується тим, що сума ймовірностей подій в ній дорівнює одиниці:

.

Дослідом може бути і зміна значення випадкової величини X, що приймає різні значення. Тоді кожне визначене значення має зміст результату, або елементарної події.

Ансамблем називається повна група подій, або сукупність станів дискретної випадкової величини , інакше, поле неспільних подій з відомим розподілом ймовірностей , що складають в сумі одиницю. Тут мається на увазі кінцева множина подій і, отже, дискретна система станів, значень, положень і так далі.

Взагалі подіями можуть бути можливих дискретних станів якої-небудь фізичної системи, наприклад значень вимірюваної величини, положень регулюючого органу, стан елементів виробничого устаткування і так далі. Їм поставлена у відповідність множина їх ймовірностей .

Формально ансамбль можна визначити як трійку , де значення випадкової величини із фіксованої множини елементів ,яким відповідає сукупність ймовірностей , таких що , . В іншому трактуванні можна записати як .

У найпростішому випадку ці події несумісні. Вони складають повну групу, у якій обов'язково реалізується одна з подій і має місце умова

.

Як правило схема ансамблю задається таблицею (матрицею) вигляд якої наведений у таблиця 2.1.

Таблиця 2.1 – Схема ансамблю подій

Дискретні стани (величини)	х1	х2	...	хi	...	хk
Ймовірності станів (величин)	p1	p2	...	pi	...	pk

В загальному ймовірності не залишаються постійними, а можуть змінюватися в часі, в залежності від умов і обставин. Тоді і статистичні характеристики (середнє значення і дисперсія) стають змінними величинами. Процеси, що описуються цими величинами, називаються нестаціонарними в статистичному змісті.

Розгледимо як джерело довільну дискретну множину X і кожному повідомленню відповідає ймовірність .

Можна сформувати інтуїтивні вимоги до деякої міри , визначеною для всіх , яку слід прийняти як міру інформації, що міститься в повідомленнях ансамблю .

- Оскільки передбачається, що ця міра визначатиме витрати, пов'язані з передачею або зберіганням повідомлень, міра має бути ненегативною.

- Оскільки неістотно, яким чином будуть інтерпретовані і використані отримані повідомлення, міра повинна однозначно визначатися тільки ймовірністю повідомлення. Тому міра , однозначно визначається .

- Виходячи з проведеного характер залежності міри від ймовірності повідомлень. Хай є множина з двох рівноімовірних повідомлень і стоїть задача кодування повідомлень цієї множини двійковими символами алфавіту A = {0,1}. Інтуїтивно ясно, що непоганий спосіб кодування полягає в тому, щоб поставити у відповідність одному з повідомлень символ 0, іншому - символ 1. Точно так для кодування 4 рівноімовірних повідомлень можна використовувати послідовності довжини 2, для 8 повідомлень - довжини 3 і так далі У цих прикладах ймовірностям 1/2, 1/4, 1/8... відповідали витрати на передачу відповідно рівні 1, 2, 3... одиницям інформаційної міри. Отже, інтуїтивно необхідно, щоб міра інформації задовольняла співвідношенню .

- Нехай задана послідовність повідомлень вибираних незалежно з одним і тим же розподілом ймовірностей {p(x)}. Із статистичної незалежності повідомлень виходить, що знання попередніх повідомлень не допомагає передбачити, якими будуть наступні. Тому витрати на передачу послідовності складаються з витрат на передачу кожного окремого повідомлення. Звідси випливає ще одна властивість інформаційної міри: .

Виходячи з вказаних вище вимог до ймовірностної міри інформації Шеннон, по аналогії з Хартлі, запропонував, наступне визначення:

Власною інформацією I(x) повідомлення x, вибираного з дискретного ансамблю , називається величина, що обчислюється за формулою

. (2.13)

Основа логарифма визначає одиницю виміру ентропії і кількості інформації. Двійкова одиниця, відповідна основі, рівній двом, називається бітом. Основі, рівній е =2,718281828…, відповідає натуральна одиниця – ніт, 1ніт = 1,44269 біт. Основі, рівній 10, відповідає десяткова одиниця – діт, 1діт=3,32193 біт. Десяткову одиницю називають також хартлі.

Найчастіше застосовують двійковий логарифм, оскільки він безпосередньо дає кількість інформації в бітах, добре узгоджується з двійковою логікою, двійковим кодуванням і двійковою (релейною) технікою. У теоретико-информационных дослідженнях часто вважають за краще ніти, оскільки натуральні логарифми зручніше диференціювати ніж десяткові.

З визначення власної інформації і властивостей логарифма безпосередньо витікають властивості власної інформації притаманні мірі Хартлі, .

Приклад 2.10.

Прогнозується температура на віддалений день (для визначеності в конкретний момент доби). Якщо на підставі яких-небудь даних відомо тільки те, що в заданий день температура не може бути нижче 12° і вище 21°, то доводиться користуватися апріорною (до дослідної) рівномірною щільністю розподілу (рис.2.7, графік а) згідно таблиці 2.2, рядок а.

З наближенням заданого дня з'являється додаткова інформація, що уточнює розподіл ймовірності (рис.2.7, графік б). Тоді щільність розподілу можна описати згідно таким чином таблиці 2.2, рядок б.

Таблиця 2.2 – Зміна розподілу при надходженні інформації

а) Рівномірний розподіл		12	13	14	15	16	17	18	19	20	21
		0,1	0,1	0,1	0,1	0,1	0,1	ο,ι	0,1	0,1	0,1
б) Нормальний розподіл		12	13	14	15	16	17	18	19	20	21
		0	0,05	0,1	0,15	0,2	0,2	0,15	0,1	0,05	0
в) Дельта-розподіл		12	13	14	15	16	17	18	19	20	21
		0	0	0	0	0	1	0	0	0	0

Очевидно, що з настанням заданого дня і години прогнозоване явище стає реалізованим, встановлюється певна температура, наприклад х - 17° (рис.2.7, графік в).Таким чином, невизначеність знімається повністю і апостеріорний (після дослідний) кінцевий розподіл набуває вигляду вказаного у таблиці 2.2, рядок в.

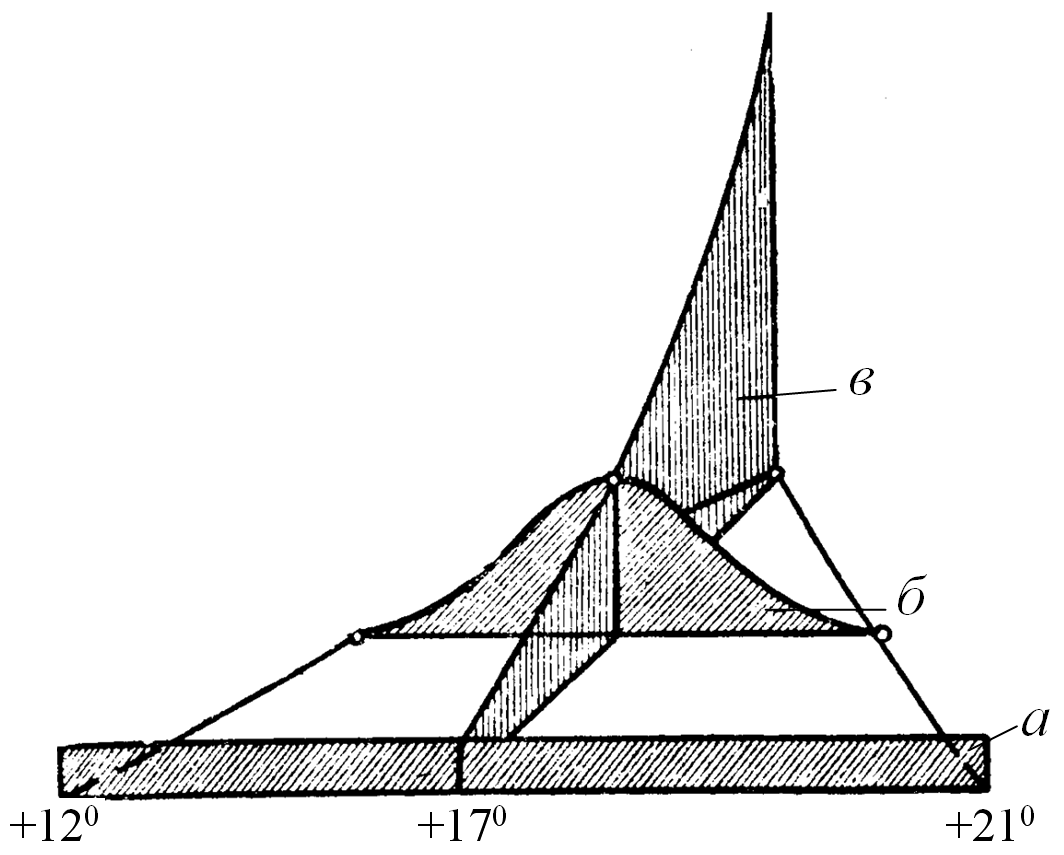
Рисунок 2.6 – Деформації щільності розподілу ймовірності

Приклад 2.11.

Послідовне зняття невизначеності. (передасться число (слово) з глибиною і довжиною представлене у двійковому коді як 011).

Крок 1. Передається 0; може бути 000, 001, 010, 011.

Крок 2. Передається 1; може бути 010, 011.

Крок 3. Передається 1; може бути 011.