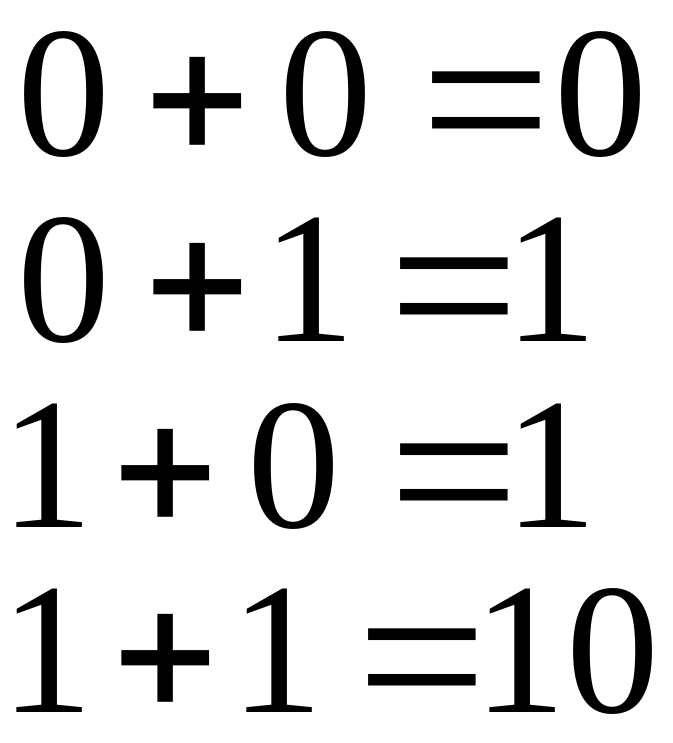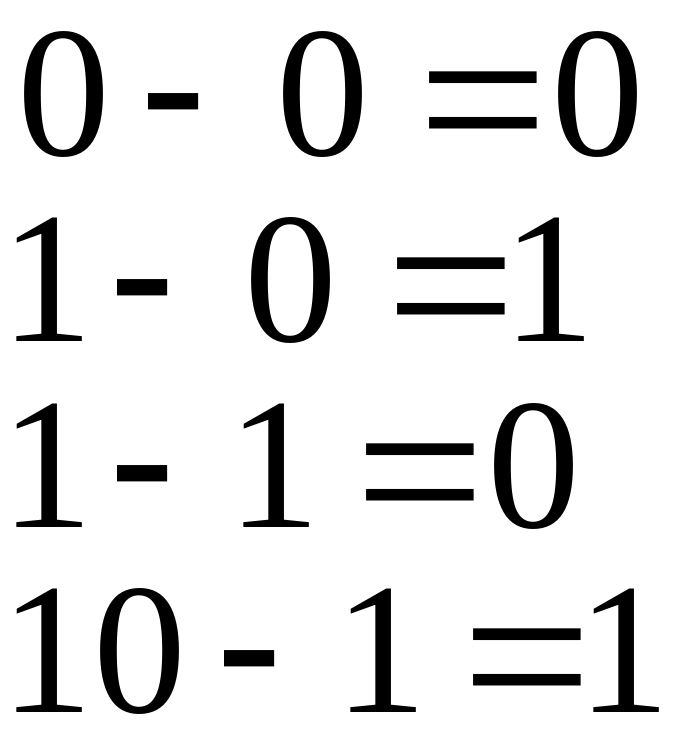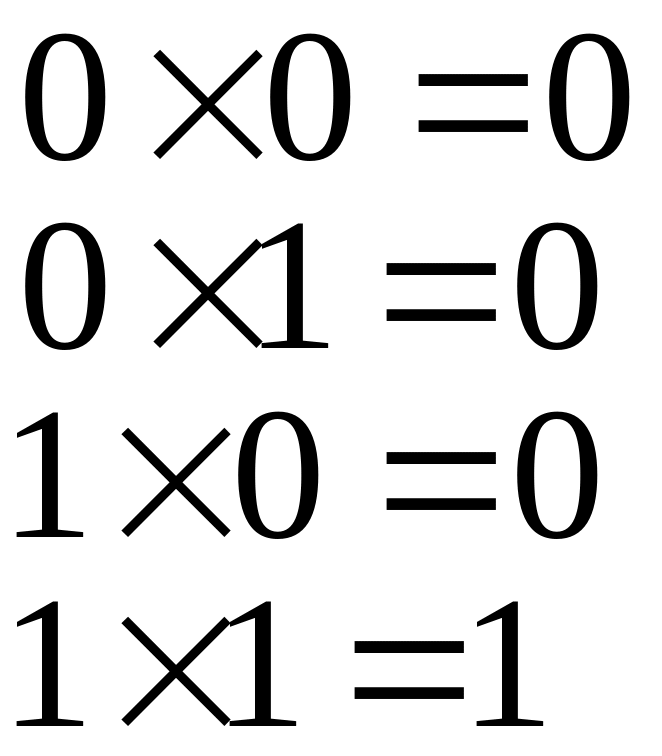6.2Кодування як процес представлення інформації в цифровому вигляді

Більшість кодів, що використовуються при кодуванні інформації без врахування статистичних властивостей джерела і завади в каналі зв'язку, заснована на системах числення.

Будь-якому дискретному повідомленню або букві повідомлення можна приписати якийсь порядковий номер. Вимір аналогової величини, що виражається в порівнянні її із зразковими засобами, також приводить до числового представлення інформації. Передача або зберігання повідомлень при цьому зводиться до передачі або зберігання чисел. Числа можна виразити в якій-небудь системі числення. Таким чином, буде отриманий одна з код, заснованих на даній системі числення.

Порівняємо системи числення і побудовані на їх основі коди з позицій вживання в системах передачі, зберігання і перетворення інформації.

Загально визнаним в даний час є позиційний принцип утворення системи числення. Значення кожного символу (цифри) залежить від його положення - позиції у ряді символів, що представляють число.

Одиниця кожного наступного розряду більше одиниці попереднього розряду в m разів, де m - основа системи числення. Повне число отримують, підсумовуючи значення по розрядах:

(5.1)

де i - номер розряду даного числа; l - кількість рядів; а_i - множник, що набуває будь-яких цілочисельних значень в межах від 0 до m-1 і що показує, скільки одиниць i-ого ряду міститься в числі.

Чим більше основа системи числення, тим менше число розрядів потрібне для представлення даного числа, а отже, і менший час для його передачі.

Проте із зростанням основи істотно підвищується вимога до лінії зв'язку і апаратурі створення і розпізнавання сигналів, відповідних різним символам. Логічні елементи обчислювальних пристроїв в цьому випадку повинні мати більшу кількість стійких станів.

Враховуючи ці обставини, доцільно вибрати систему числення, яка забезпечує мінімум добутку кількості різних символів на кількість розрядів для представлення будь-якого числа. Знайдемо цей мінімум але графіку (рис.5.1), де показаний зв'язок між величинами і при відтворенні певного достатньо великого .

1	60000	60000
2	4	32
3	10	30
4	8	32
16	4	64
40	3	120
60000	1	60000

Рисунок 5.1 – Залежність кількості розрядів у числі від основи системи числення

З графіка виходить, що найбільш ефективною системою числення є трійкова. Трохи поступається їй двійкова і четверкова. Системи з основою 10 і більше істотніше менш ефективні. Порівнюючи ці системи з точки зору зручності фізичної реалізації відповідних їм логічних елементів і простоти виконання в них арифметичних і логічних дій, перевагу необхідно віддати двійковій системі. Дійсно, логічні елементи, відповідні цій системі, повинні мати всього два стійкі стани. Завдання розрізнення сигналів зводиться в цьому випадку до завдання виявлення (є імпульс чи ні імпульсу), що значно простіше.

Арифметичні і логічні дії також найпростіше здійснюються в двійковій системі. У таблиці додавання, віднімання і множення входить всього по чотири рівності:

Правила додавання:	Правила віднімання:	Правила множення

Найбільш поширена при кодуванні і декодуванні логічна операція – це додавання по модулю. У двійковій системі вона також найбільш проста і визначається рівностями:

.

Знайдемо, наприклад, десятковий еквівалент двійкового числа 1001. Після першої одиниці зліва стоїть 0. Подвоюємо цю одиницю. Отримуємо число 2. Цифрою наступного молодшого розряду також є 0. Подвоюючи число 2, отримуємо 4. У самому молодшому розряді коштує одиниця. Подвоюючи число 4 і додаючи 1, остаточно отримуємо 9.

Отже, для передачі і проведення логічних і арифметичних операцій найбільш доцільний двійковий код. Проте він незручний при введенні і виведенні інформації, оскільки важко оперувати з незвичними двійковими числами. Крім того, запис таких чисел на папері виявляється дуже громіздким. Тому, окрім двійкової набули поширення системи, які з одного боку легкий зводяться як до двійкової, так і до десяткової систем, а з іншого боку – дають компактніший запис.

До таких систем відноситься вісімкова, шістнадцяткова і двійково-десяткова.

У вісімковій системі для запису всіх можливих чисел використовується вісім цифр, від 0 до 7 включно. Переклад чисел з вісімкової системи в двійкову украй простий і зводиться до заміни кожної вісімкової цифри рівним їй трьохрозрядним числом. Наприклад, для вісімкового числа 745 отримуємо:

7	4	5
111	100	101

Оскільки у вісімковій системі числа є коротшими, ніж в двійковій, вона широко використовується як допоміжна система при програмуванні.

Аби зберегти переваги двійкової системи і зручність десяткової системи, використовують двійково-десяткові коди. У такому коді кожна цифра десяткового числа записується у вигляді чотири розрядного двійкового числа (тетради). За допомогою чотирьох розрядів можна утворити 16 різних комбінацій, з яких будь-які 10 можуть скласти двійково-десятковий код.

Серед кодів, що відходять від систем числення, велике практичне значення мають також коди, в яких при переході від одного числа до іншого зміна відбувається лише в одному розряді. Найбільшого поширення набув код Грея, часто званий циклічним або рефлексно-двійковим. Код Грея використовується при аналого-кодовому перетворенні, де він дозволяє звести до одиниці молодшого розряду помилку неоднозначності при зчитуванні. Комбінації коди Грея, що відповідають десятковим числам від 0 до 15, приведені в таблиці 5.1.

Таблиця 5.1 – Комбінації коду Грея, що відповідають десятковим числам

Число в десятковому коді	Код Грея	Число в десятковому коді	Код Грея	Число в десятковому коді	Код Грея
0	0000	6	0101	11	1110
1	0001	7	0100	12	1010
2	0011	8	1100	13	1011
3	0010	9	1101	14	1001
4	0110	10	1111	15	1000
5	0111

Правила переводу числа з коду Грея в звичайний двійковий зводиться до наступного: перша одиниця з боку старших розрядів залишається без зміни, подальші цифри (0 і 1) залишаються без зміни, якщо кількість одиниць, що їм передували, парна, і інвертуються, якщо кількість одиниць непарна.

Приклад 5.1

Перевести з число у коді Грея 1010, у звичайний двійковий код.

Розв’язок:

Перша одиниця зліва переписується. Наступна цифра буде одиницею, оскільки в цьому розряді коду Грея стоїть 0 і попереду лише одна одиниця. Далі необхідно записати нуль, оскільки в наступному розряді вихідного числа стоїть 1 і попереду знову є лише одна одиниця. Оскільки перед останньою цифрою числа в коді Грея коштують дві одиниці, то вона повинна залишитися незмінною, тобто нулем. Таким чином, числу 1010 в коді Грея відповідає звичайне двійкове число 1100.