6.4.4Кодова відстань

При взаємно незалежних помилках найбільш ймовірний перехід в кодову комбінацію, що відрізняється від даної в найменшому числі символів.

Міра відмінності будь-яких двох кодових комбінацій характеризується відстанню між ними в сенсі Хеммінга або просто кодовою відстанню.

Кодова відстань d дорівнює числу символів, в яких комбінації відрізняються одна від одної.

Аби отримати кодову відстань між двома комбінаціями двійкових кодів, досить підрахувати число одиниць в сумі цих комбінацій по модулю 2. Наприклад

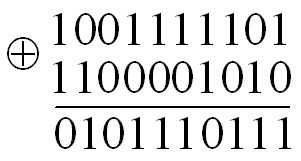
де .

Мінімальну відстань, узяту по всіх парах кодових дозволених комбінацій коди, називають мінімальною кодовою відстанню.

Повніше уявлення про властивості коди дає матриця відстаней D, елементи якої дорівнюють відстаням між кожною парою зі всіх m дозволених комбінацій.

Приклад 5.3

Представити симетричною матрицею кодових відстаней код:

Розв’язок: Мінімальна кодова відстань для коду . Симетрична матриця четвертого порядку кодових відстаней для заданого коду наведена у вигляді таблиці 5.8.

Таблиця 5.8 – Матриці кодових відстаней

Коди
		000	001	010	111
	000	0	1	1	3
	001	1	0	2	2
	010	1	2	0	2
	111	3	2	2	0

Декодування після прийому даних виходить з того, що прийнята кодова комбінація ототожнюється з тією дозволеною, яка знаходиться від неї на найменшій кодовій відстані.

Таке декодування називається декодуванням по методу максимальної правдоподібності.

Вочевидь, що при кодовій відстані всі кодові комбінації є дозволеними.

Наприклад, при дозволені комбінації утворюють наступну множину:

000, 001, 010, 011, 100, 101, 110, 111.

Будь-яка одиночна помилка трансформує дану комбінацію в іншу дозволену комбінацію. Це випадок коди безнадлишкового, коду, який не володіє коректуючою здатністю.

Якщо , то жодна з дозволених кодових комбінацій при одиночній помилці не переходить в іншу дозволену комбінацію. Наприклад, підмножина дозволених кодових комбінацій може бути утворена за принципом парності у ній числа одиниць. Наприклад, для :

000, 011, 101, 110 – дозволені комбінації;

001, 010, 100, 111 – заборонені комбінації.

Код виявляє одиночні помилки, а також інші помилки непарної кратності (при потрійні).

У загальному випадку при необхідності виявляти помилки кратності до r включно мінімальна хэммінгова відстань між дозволеними кодовими комбінаціями має бути принаймні на одиницю більше r, тобто

. (5.7)

Дійсно, в цьому випадку помилка, кратність якої не перевищує r, не в змозі перевести одну дозволену кодову комбінацію в іншу.

Для виправлення одиночної помилки кодової комбінації необхідно співставити підмножину заборонених кодових комбінацій.

Щоб ці підмножини не перетиналися, хэммінгова відстань між дозволеними кодовими комбінаціями має бути не менше трьох. При за дозволені кодові комбінації можна, наприклад, прийняти 000 і 111. Тоді дозволеній комбінації 000 необхідно приписати підмножину заборонених кодових комбінацій 001, 010, 100, що утворюються в результаті подвійної помилки в комбінації 000.

Подібним чином дозволеній комбінації 111 необхідно приписати підмножину заборонених кодових комбінацій: 110, 011, 101, що утворюються в результаті виникнення одиничної помилки в комбінації 111 (рис.5.3):

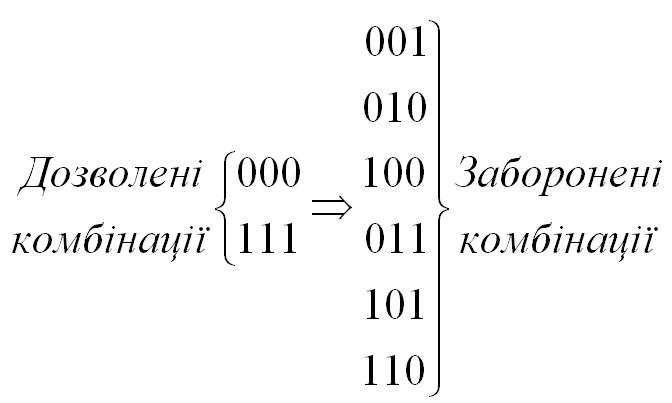
Рисунок 5.3 – Відповідність між кодовими комбінаціями

У загальному випадку для забезпечення можливості виправлення всіх помилок кратності до s включно при декодуванні по методу максимальної правдоподібності, кожна з помилок повинна приводити до забороненої комбінації, що відноситься до підмножини вихідної дозволеної кодової комбінації.

Будь-яка n-розрядна двійкова кодова комбінація може бути інтерпретована як вершина m-мірного одиничного куба.

При кодові комбінації розташовуються у вершинах квадрата (рис.5.4).

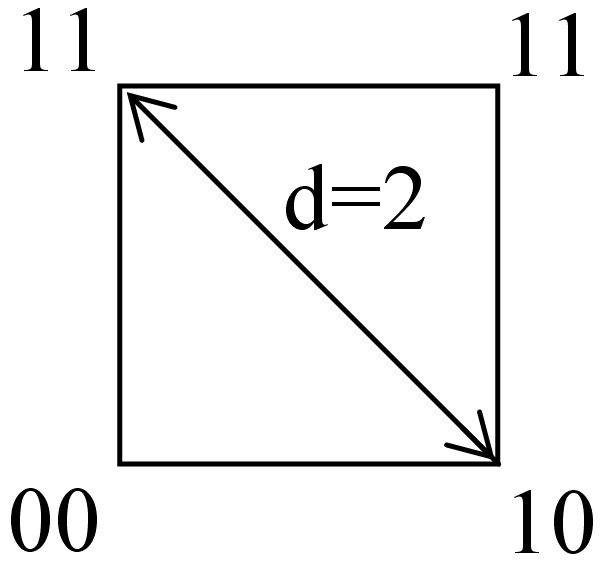
Рисунок 5.4 – Геометрична інтерпретація двох розрядної кодової комбінації

При кодові комбінації розташовуються у вершинах одиничного куба (рис.5.5).

У загальному випадку n-мірний одиничний куб має вершин, що дорівнює найбільшому можливому числу кодових комбінацій.

Така модель дає просту геометричну інтерпретацію кодовій відстані між окремими кодовими комбінаціями, вона відповідає найменшому числу ребер одиничного куба, які необхідно пройти, аби попасти від однієї комбінації до іншої.

Помилка буде не лише виявлена, але і виправлена, якщо спотворена комбінація залишається ближчою до первинної, чим до будь-якої іншої дозволеної комбінації, тобто повинна виконуватись умова:

або . (5.8)

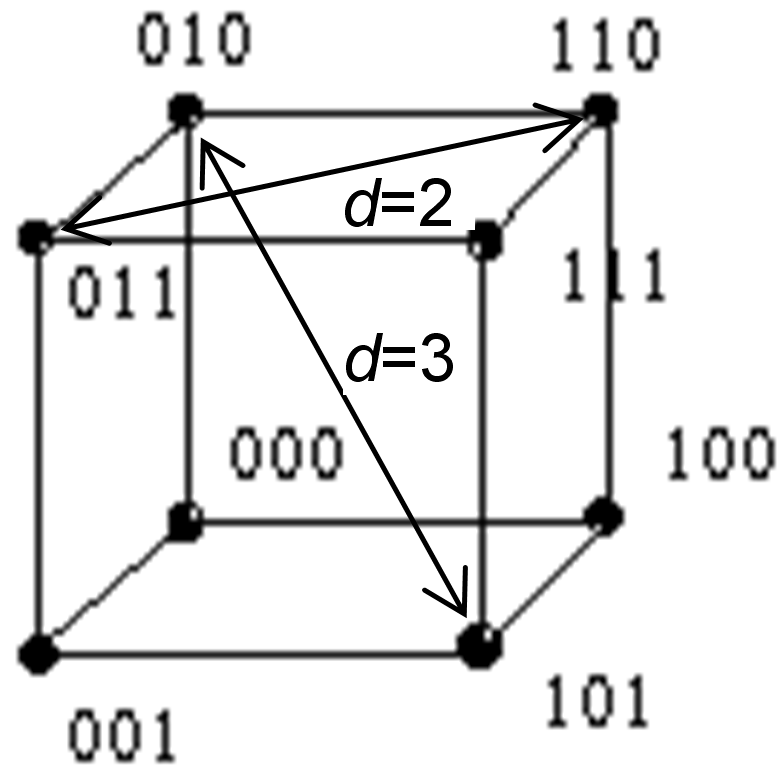
Рисунок 5.5 – Геометрична інтерпретація трьох розрядної кодової комбінації

У загальному випадку n-мірний одиничний куб має вершин, що дорівнює найбільшому можливому числу кодових комбінацій.

Така модель дає просту геометричну інтерпретацію кодовій відстані між окремими кодовими комбінаціями, вона відповідає найменшому числу ребер одиничного куба, які необхідно пройти, аби попасти від однієї комбінації до іншої.

Помилка буде не лише виявлена, але і виправлена, якщо спотворена комбінація залишається ближчою до первинної, чим до будь-якої іншої дозволеної комбінації, тобто повинна виконуватись умова:

або . (5.9)

У загальному випадку для того, щоб код дозволяв виявляти всі помилки кратності r і виправляти всі помилки кратності s ( ), його кодова відстань повинна задовольняти нерівності

. (5.10)

Метод декодування при виправленні одиночних незалежних помилок можна пояснити таким чином. У підмножину кожної дозволеної комбінації відносять всі вершини, що лежать у сфері з радіусом і центром у вершині, що відповідає даній дозволеній кодовій комбінації. Якщо в результаті дії завади комбінація переходить в точку, що знаходиться усередині сфери, то така помилка може бути виправлена.

Якщо завада зміщує точку дозволеної комбінації на границю двох сфер (відстань ) або більше (але не в крапку, що відповідає іншій дозволеній комбінації), то таке спотворення може бути виявлене.

Для кодів з незалежним спотворенням символів кращі коректуючи коди, це такі, у яких точки, що відповідають дозволеним кодовим комбінаціям, розташовані в просторі рівномірно.

Проілюструємо побудову коректуючого коду на прикладі. Нехай вихідний алфавіт, що складається з чотирьох букв, закодований двійковим кодом: Цей код використовує всі можливі комбінації довжини 2, і тому не може виявляти помилки (оскільки ).

Припишемо до кожної кодової комбінації один елемент 0 або 1 так, щоб число одиниць було парне, тобто

(5.10)

Для цього коду , і, отже, він здатний виявляти всі однократні помилки. Оскільки будь-яка заборонена комбінація містить непарне число одиниць, то для виявлення помилки досить перевірити комбінацію на парність (наприклад, сумуванням по модулю 2 цифр кодової комбінації). Якщо число одиниць в слові парне, то сума по модулю 2 його розрядів буде 0, якщо непарне – те 1. Ознакою парності називають інверсію цієї суми.

Розглянемо загальну схему організації контролю по парності (рис.5.6). На n-входовому елементі (інверсія додавання по модулю 2) формується ознака парності Р числа, який як додатковий, -й контрольний розряд (parity bit) вирушає разом з передаваним словом в лінію зв'язку або пристрій, що запам'ятовує. Передаване -розрядне слово має завжди непарне число одиниць. Якщо у вихідному слові воно було непарним, то інверсія функції від такого слова дорівнює 0, і нульове значення контрольного розряду не міняє число одиниць при передачі слова. Якщо ж число одиниць у вихідному слові було парним, то контрольний розряд Р для такого числа дорівнюватиме 1, і результуюче число одиниць в передаваному -розрядному слові стане непарним. Контроль, коли по лінії передається непарне число одиниць, по строгій термінології називають контролем по непарності.

Рисунок 5.5 – Схема організації контролю по парності

На приймальному кінці лінії або з пам'яті від отриманого -розрядного слова знову береться згортка по парності. Якщо значення цієї згортки дорівнює 1, то або в передаваному слові, або в контрольному розряді при передачі або зберіганні сталася помилка. Настільки простий контроль не дозволяє виправити помилку, але він, принаймні, дає можливість при виявленні помилки виключити невірні дані, зажадати повторну передачу і так далі

Систему контролю можна побудувати на основі не лише інверсії функції , але і прямої функції (строго контроль по парності). Проте, в цьому випадку вихідний код “всі нулі” матиме контрольний розряд, рівний 0. У лінію відправиться посилка з суцільних нулів, і на приймальному кінці вона буде невідмінна від вельми небезпечної несправності – повної пропажі зв'язку. Тому контроль по парності в своєму чистому вигляді майже ніколи не застосовують, контрольний розряд формують як парності, і в нестрогій термінології “контролем по парності” називають те, що, строго кажучи, насправді є контролем по непарності.

Контроль по парності заснований на тому, що одиночна помилка (неважливо – пропажа одиниці або поява її на лінії) інвертує ознаку парності. Проте дві помилки проінвертують його двічі, тобто залишать без зміни, тому подвійну помилку контроль по парності не виявляє. Міркуючи аналогічно, легко прийти до висновку, що контроль по парності виявляє всі непарні помилки і не реагує на будь-які парні. Пропуск парних помилок – це не який-небудь дефект системи контролю. Це наслідок гранично малій надлишковості, рівній всього одному розряду. Для глибшого контролю потрібний відповідно і велика надлишковість. Якщо помилки один від одної не залежать, то і з невиявлених найчастіше зустрічатиметься подвійна помилка, а при ймовірності одиночної помилки, рівній р, ймовірність подвійною буде . Оскільки в нормальних цифрових пристроях , невиявлені подвійні помилки зустрічаються значно рідше, ніж виявлені одиничні. Тому далі при такому простому контролі якість роботи пристрою істотно зростає. Однак це вірно лише для взаємно незалежних помилок.

Ознаки парності можна використовувати для контролю лише незмінних даних. При виконанні над даними яких-небудь логічних операцій ознаки парності слів загалом змінюються, і спроби компенсувати ці зміни виявляються неефективними. Щасливе виключення – операція арифметичного додавання: сума по модулю 2 ознак парності двійкових доданків і всіх, виниклих в процесі додавання перенесень, дорівнює ознаці парності коду арифметичної суми цих доданків.

Контроль по парності – найдешевший за апаратурними витратами вид контролю, і застосовується він дуже широко. Практично будь-який канал передачі цифрових даних або пристрій, що запам'ятовує, якщо вони не мають якого-небудь сильнішого методу контролю, захищені контролем по парності.

Продовжимо розгляд прикладу побудови коректуючого методу. Аби код був здатний і виправляти однократні помилки, необхідно добавити ще не менше двох розрядів. Це можна зробити різними способами, наприклад, у коді (5.10) приписати перші дві цифри у двох останніх розрядах

Матриця кодових відстаней цього коду наведена у таблиці 5.9.

Таблиця 5.9 – Матриці кодових відстаней

Коди
		00000	01101	10110	11011
	00000	0	3	3	4
	01101	3	0	4	3
	10110	3	4	0	3
	11011	4	3	3	0

Видно, що тут , що згідно (5.10) відповідає нерівності .