3.3.4Ентропія об’єднання, умовна ентропія

При оцінці невизначеності вибору двох випадкових величин необхідно враховувати статистичні зв'язки, які в більшості випадків мають місце:

– між станами двох або декількох джерел, об'єднаних в рамках однієї системи;

– між станами, що послідовно вибираються з одного джерела.

Об'єднанням називається сукупність двох і більше взаємозалежних ансамблів дискретних випадкових станів (всіх можливих комбінацій цих станів).

Нехай задане об'єднання, що складається з двох ансамблів X і Y, зв'язаних між собою імовірнісними залежностями.

Схема ансамблю X:

Схема ансамблю Y:

.

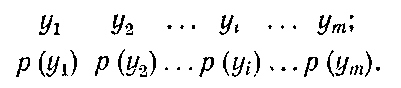Схема об'єднання X і Y:

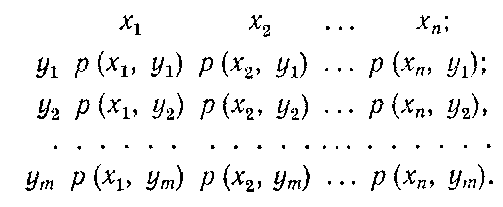
Очевидно, що

і ,

.

Ймовірність добутку (збігу) спільних залежних подій н дорівнює добутку безумовної ймовірності або на умовні ймовірності або , формула Бейса:

. (2.30)

Звідси знаходяться умовні ймовірності

, (2.31)

залежно від того, яка подія є причиною, а яка – наслідком.

З об'єднанням пов'язані поняття безумовної, умовної, спільної і взаємної ентропії. Їх інколи називають також неалежною, залежною, корельованою і взаємною ентропією, або трансінформациією.

Введені поняття зручно проілюструвати прикладом передачі інформації по схемі (рис.2.7).

Рисунок 2.7 – Передача дискретної інформації по каналу зв’язку

Послідовність символів , що створюється джерелом, може зазнавати спотворення на шляху до приймача. Символ може бути прийнятий не лише як однозначно йому відповідний символ , але і як будь-який з можливих символів з відповідною ймовірністю.

Різні види ентропії в даній схемі мають наступний сенс:

– безумовна ентропія джерела X, або середня кількість інформації на символ, що видається джерелом.

– безумовна ентропія приймача Y, або середня кількість інформації на символ, що отримується приймачем;

– умовна ентропія Y відносно X, або міра кількості інформації в приймачі, коли відомо, що передається X;

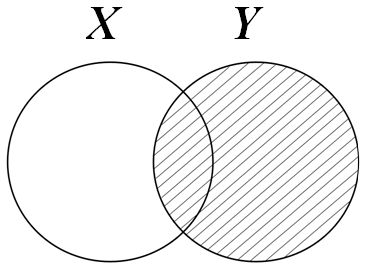
– умовна ентропія X відносно Y, або міра кількості інформації про джерело, коли відомо, що приймається Y

– взаємна ентропія системи передавання - сприйняття в цілому, або середня інформація на пару (переданого і прийнятого) символів;

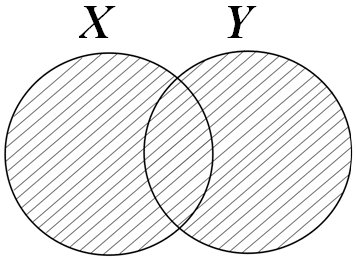
– сумісна ентропія, або середня кількість інформації на символ, що видається джерелом і символ, що отримується приймачем.

Якщо в системі немає втрат і спотворень, то умовні ентропії дорівнюють нулю

,

а кількість взаємної інформації дорівнює ентропії або джерела, або приймача

.

На основі статистичних даних може бути встановлені ймовірності подій за умови, що мали місце події , а саме .Тоді частинна умовна ентропія буде рівна:

. (2.32)

Далі потрібно підрахувати середнє значення для всіх переданих символів . Це буде умовна ентропія каналу

,

або в розгорнутому вигляді

. (2.33)

Аналогічно можна отримати вираз для умовної ентропії , що враховує умовні ймовірності :

. (2.34)

Безумовна ентропія ансамблю X:

, (2.35)

а безумовна ентропія ансамблю X

. (2.36)

В реальних умовах незалежність елементарних повідомлень, що виробляються джерелом, - явище досить рідкісне. Частіше буває навпаки - сильний детермінований або статистичний зв'язок між елементами повідомлення одного або декількох джерел.

Наприклад, при передачі тексту ймовірності появи окремих букв залежать від того, які букви їм передували. Для українського тексту, наприклад, якщо передана буква "П", ймовірність того, що наступною буде "А", набагато вище, ніж "Н" і так далі Подібна ж картина спостерігається при передачі зображень - сусідні елементи зображення мають зазвичай майже однакову яскравість і колір.

При передачі і зберіганні даних часто також має місце декілька джерел, що формують статистично зв'язані оди з одним повідомлення. Повідомлення, що виробляються такими джерелами, називаються складними повідомленнями, а самі джерела - джерелами з пам'яттю.

Очевидно, що при визначенні ентропії і кількості інформації в повідомленнях, елементи яких статистично зв'язані, не можна обмежуватися тільки безумовною ймовірністю - необхідно обов'язково враховувати також умовну ймовірність появи окремих повідомлень.

Визначимо ентропію складного повідомлення, що виробляється двома залежними джерелами (подібним же чином визначається ентропія складного повідомлення, що виробляється одним джерелом з пам'яттю).

Нехай повідомлення першого джерела приймають значення з ймовірністю, відповідно, , повідомлення другого з ймовірністю .

Спільну ентропію двох джерел X і Y визначається як:

, (2.37)

де - ймовірність спільної появи повідомлень і . Оскільки спільна ймовірність за формулою Байеса визначається як

, (2.38)

то вираз для спільної ентропії можна записати в наступному вигляді:

Оскільки передачі повідомлення обов'язково відповідає передача будь-якого одного з повідомлень ансамблю Y, то

і спільна ентропія визначиться як

, (2.39)

де частинна умовна ентропія (див.(2.32)) відображає ентропію повідомлення Y за умови, що мало місце повідомлення . Другий доданок в останньому виразі є усереднюванням по всіх повідомленнях і називається середньою умовною ентропією джерела Y за умови передачі повідомлення X. Остаточно:

. (2.40)

Таким чином, спільна ентропія двох повідомлень дорівнює сумі безумовної ентропії одного з них і умовної ентропії другого.

Аналогічно можна показати, що основні властивості ентропії складних повідомлень співпадають з основними властивостями ентропії при передачі дискретної інформації по каналу зв’язку (рис.2.7).

Отже, за наявності зв'язку між елементарними повідомленнями ентропія джерела зменшується, причому тим більше чим сильніше зв'язок між елементами повідомлення. Звідси, можна зробити наступні висновки щодо ступеня інформативності джерел повідомлень:

• Ентропія джерела і кількість інформації тим більше, чим більше розмір алфавіту джерела.

• Ентропія джерела залежить від статистичних властивостей повідомлень. Ентропія максимальна, якщо повідомлення джерела рівноймовірні і статистично незалежні.

• Ентропія джерела, що виробляє нерівноімовірні повідомлення, завжди менше максимально досяжної.

• За наявності статистичних зв'язків між елементарними повідомленнями (пам'яті джерела) його ентропія зменшується.

Приклад2.12.

Нехай задано матрицю сумісних ймовірностей появи повідомлень двох джерел А та В з алфавітами а_i та b_j, де :

. (2.41)

Оскільки – безумовні ймовірності, для них виконується закон нормування

Окрема розгортка по рядках (по i) без зміни j «поглинає» алфавіт а_i і дає безумовну ймовірність р(b_j), тобто імовірнісну міру для джерела В:

0,2 + 0 + 0,1 = 0,3 =р(b₁) при j=1;

0 + 0,2 + 0,1 = 0,3 = р(b₂) при j = 2; (2.42)

0,1 + 0,1 + 0,2 = 0,4 = р(b₃) при j=3.

Перевіримо нормування:

р (b₁) +p (b₂) +р (b₃)=0,3 + 0,3 + 0,4=1.

Окрема згортка по стовпцях (за j) без зміни i «поглинає» алфавіт b_j і дає безумовну ймовірність р (а_i), тобто імовірнісну міру для джерела А:

0,2 + 0 + 0,1 = 0,3 = р(а₁) при i= 1;

0 + 0,2 + 0,1 = 0,3 =p(a₂) при i = 2; (2.43)

0,1 + 0,1 + 0,2 = 0,4 = р(a₃) при i = 3.

Перевіряємо нормування:

р(a₁) + р(а₂) + р(а₃)=0,3 + 0,3 + 0,4 = 1.

З урахуванням (2.31) на підставі (2.30), для даного випадку за формулою:

,

можна отримати матрицю умовних ймовірностей:

. (2.44)

Перевірка на виконання закону нормування (2.26) дає позитивну відповідь, тобто

2/3 + 0 + 1/3 = 3/3 = 1 = p(a₁|b₁) + p(a₂|b₁)+p(a₃|b₁) при j= 1;

0 + 2/3 + 1/3 = 3/3 = 1 = p(a₁|b₂) + p(a₂|b₂)+p(a₃|b₂) при j= 2;

0,25 + 0,25 + 0,5 = 1 =p(a₁|b₃) + p(a₂|b₃)+p(a₃|b₃) при j= 3;

Отже, кожний рядок (2.44) є розподілом повідомлень а_i, спотвореним через статистичний вплив повідомлень b_j.

Аналогічно за формулою

можна отримати матрицю умовних ймовірностей:

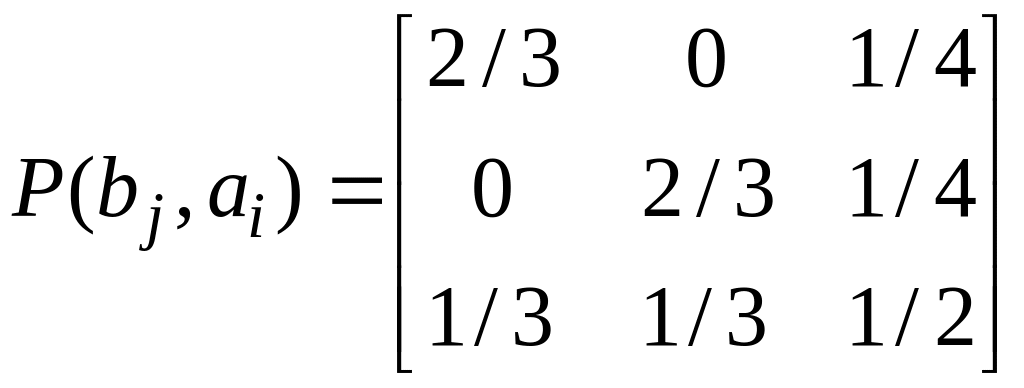. .45)

Перевірка виконання закону нормування (2.24) дає позитивну відповідь, тобто

2/3+0+1/3 = 3/3 = 1 = р(b₁|а₁)+р(b₂|a₁)+р(b₃|a₁) при i =1;

0+2/3+1/3 = 3/3 = 1 = p(b₁|а₂)+р(b₂|а₂)+р(b₃|а₂) при i =2;

0,25+0,25+0,5 = 3/3=1 = р(b₁|а₃)+р(b₂|а₃)+р(b₃|а₃) при i =3.

Таким чином, кожний стовпець (2.45) є розподілом повідомлень b_j, спотвореним через статистичний вплив повідомлень а_і.

Тепер, маючи дані , за аналогом (2.35):

,

розрахуємо безумовну ентропію джерела А:

Н (А)=-(0,3log0,3 + 0,3log0,3 + 0,4log0,4)=

= 1,57095 біт/ повідомлення.

Аналогічно, маючи дані за аналогом (2.36):

,

розрахуємо безумовну ентропію джерела В:

Н (В)=-(0,3log0,3 + 0,3log0,3 + 0,4log0,4) =

= 1,57095 біт/повідомлення.

У розглядуваному прикладі виконається рівність Н(В)=Н(А) так як збігаються розподіли безумовних ймовірностей. До речі, максимального значення Н(А) та H(В) досягли б при рівно ймовірному розподілі ймовірностей, тобто при p (а_i) = 1/3 та р (b_j)=1/3 для .

Тоді було б

H_mаx (А)=H_mах(В)=-log₂(1/k)=log₂ k=log₂ 3 =

= 1,58496 біт/повідомлення.

Як бачимо, максимальна ентропія перевищує значення безумовної ентропії при нерівномірному розподілі ймовірностей.

Часткові умовні ентропії джерела А згідно аналога (2.32):

з урахуванням (2.45) становитиме

H(A|b₁) = = 0,91829 біт/повідомлення;

H(A|b₂) = 0,91829 біт/повідомлення;

H(A|b₃) = = 1,5 біт/повідомлення.

Загальна умовна ентропія джерела А відносно джерела В

А згідно аналога (2.33):

, (2.46)

становитиме

=1,15097 біт/повідомлення.

Часткова умовна ентропія джерела В згідно аналога (2.32):

становитиме

H(B|а₁) = 0,91829 біт/повідомлення;

H(B|а₁)=0,91829 біт/повідомлення;

H(B|а₁) = 1,5 біт/ повідомлення.

Загальна умовна ентропія джерела В відносно джерела А згідно аналога (2.33):

(2.47)

= 1,15097 біт/повідомлення.

Відзначимо окремо такі властивості умовної ентропії:

– Якщо джерела повідомлень А та В статистичне незалежні, то умовна ентропія джерела А відносно джерела В дорівнює безумовній ентропії джерела А й навпаки:

, ).

– Якщо джерела повідомлень А та В настільки статистично взаємозв'язані, що виникнення одного з повідомлень спричинює безумовну появу іншого, то умовні ентропії їх дорівнюють нулю:

.

– Ентропія джерела взаємозалежних повідомлень (умовна ентропія) менша від ентропії джерела незалежних повідомлень (безумовна ентропія).

– Максимальну ентропію мають джерела взаємонезалежних рівноймовірних повідомлень, умовна ентропія яких дорівнює нулю, а ймовірність появи символів алфавіту , де h - кількість повідомлень в алфавіті.

Приклад 2.13.

Розглянемо джерело з алфавітом, що складається з букв української мови а, б, в, ...., ю, я. Для простоти, приймемо що розмір алфавіту джерела (глибину) .

Якби всі букви алфавіту мали однакову ймовірність і були статистично незалежні, то середня ентропія, що доводиться на один символ, склала б

.

Якщо врахувати лише різну ймовірність зустрічі букв в тексті (неважко перевірити, що так воно і є), розрахункова ентропія складе

.

З врахуванням кореляції (статистичному зв'язку) між двома і трьома сусідніми буквами (після букви “П” частіше зустрічається “A” і дуже рідко – “Ц” і “Ю”) ентропія зменшиться, відповідно, до

і .

Нарешті, якщо врахувати кореляцію між вісьма і більш символами, ентропія зменшиться до

,

і далі залишається без змін.

Виникає законне питання: чи потрібно займати носій інформації або канал зв'язку передачею символів, що практично не несуть інформації, або ж можливе таке перетворення початкового повідомлення, при якому інформація "втискувалася" б в мінімально необхідне для цього число символів?

Виявляється, не лише можна, але і необхідно. Сьогодні багато з існуючих радіотехнічних систем передачі інформації і зв'язку просто не змогли б працювати, якби в них не проводилося такого роду кодування. Не було б цифрового стільникового зв'язку стандартів GSM і CDMA. Не працювали б системи цифрового супутникового телебачення, дуже неефективної була б робота Internet, а вже про те, щоб глянути відеофільм або послухати хорошу музику з лазерного диска, не могло бути і мови. Все це забезпечується ефективним або економним кодуванням інформації в даних системах.