6. Математические модели сигналов. Тестовые сигналы. Дельта–функция. Функция Хэвисайда.

Гармонический сигнал. Гармонический сигнал описывает простейший колебательный процесс. Примеры – колебания маятника, равномерное круговое движение, переменный ток и напряжение в сетях электропитания и т.д. Математическая модель гармонического сигнал задается в следующем виде x(t)=U cos(ω₀t+φ₀) = U cos ψ(t), , где U – амплитуда; ω₀ – угловая частота (скорость) колебания; φ₀ – начальный сдвиг фазы сигнала; ψ(t)= (ω₀t+φ₀) – полная фаза сигнала.

Спектр гармонического сигнала является линейчатым и содержит единственную составляющую – гармонику на частоте ω₀. Следовательно, спектр гармонического сигнала:

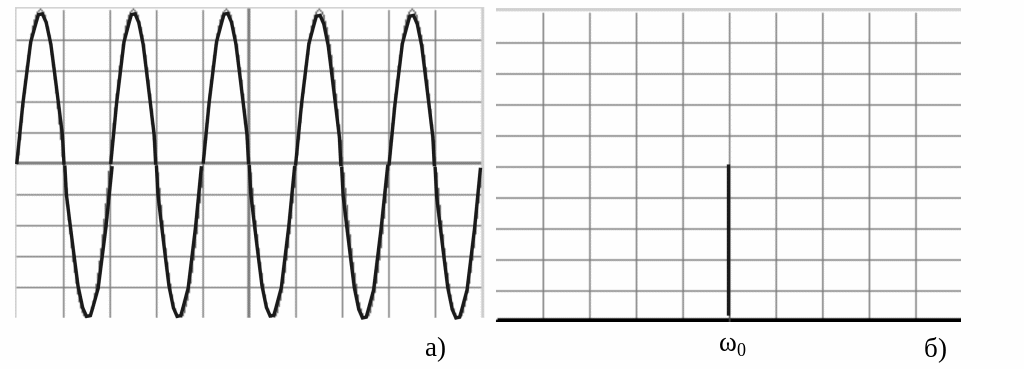
Радиосигнал. Модель радиосигнала описывают следующим образом: x(t)=U(t)cos(ω₀t+φ(t)+φ₀)= U(t)cos ψ(t), , где U(t) – огибающая функция, ψ(t) – полная фаза радиосигнала, φ(t) – фазовая функция, ω₀ – несущая частота, φ₀– начальная фаза.

Гармоническая функция является простейшим радиосигналом (U(t)= U=const, φ(t)=0). Спектр радиосигнала: S(ω)=0.5{S_U(ω+ω₀)+S_U(ω-ω₀)}, где S_U(ω) – спектр огибающей функции.

Одиночный прямоугольный видеоимпульс. Математическая модель одиночного прямоугольного видеоимпульса во временной области:

, где U – амплитуда импульса, τ – длительность импульса.

Спектр одиночного видеоимпульса является сплошным и представляет собой непрерывную периодическую функцию частоты, симметричную относительно частоты ω=0: . За эффективную ширину амплитудного спектра прямоугольного видеоимпульса принимают интервал .

Отрезок колебания. Отрезок колебания может быть представлен как гармонический сигнал с частотой ω₀, начальной фазой φ₀, который задан на ограниченном временном интервале (0; τ). Отрезок колебания называют также прямоугольным радиоимпульсом. Во временной области отрезок колебания: , где U – амплитуда сигнала, τ – длительность сигнала, при этом период сигнала .

Спектр отрезка колебания является непрерывной периодической функцией частоты вида , симметричной относительно частоты ω₀: . (1.0)

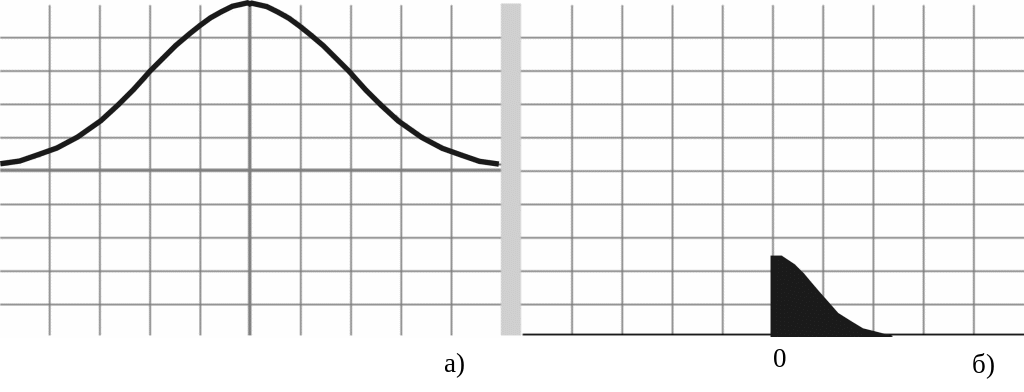
Гауссов импульс. Гауссов импульс во временной области имеет «колокольную» форму и описывается следующим образом , , где U – амплитуда импульса; α – коэффициент сжатия импульса: ; τ_эф – эффективная длительность импульса. Спектр гауссова импульса является сплошным и представляет собой непрерывную гауссовскую функцию частоты, которая имеет колоколообразную форму: . Эффективная ширина спектра гауссова импульса определяется из соотношения .

Периодическая последовательность видеоимпульсов. Математическая модель последовательности видеоимпульсов во временной области описывается следующим образом: , k=0,1,2… ; , T > τ,

где r(t) – финитный на интервале T сигнал, T – период последовательности, U и τ – соответственно, амплитуда и длительность каждого из видеоимпульсов.

Спектр последовательности видеоимпульсов является линейчатым и представляет собой дискретную периодическую функцию, симметричную относительно частоты ω=0. Амплитудный спектр представляет собой дискретную последовательность A_k: , k=0,1,2… За эффективную ширину амплитудного спектра последовательности прямоугольных видеоимпульсов принимают интервал : Δω_эф=2π/τ .

Периодическая последовательность радиоимпульсов. Последовательность радиоимпульсов можно представить в виде последовательности видеоимпульсов, каждый из которых «заполнен» гармоническим сигналом. Математическая модель последовательности радиоимпульсов: , k=0,1,2…, , T > τ > 2π/ ω₀, где r(t) – финитный на интервале T сигнал; T – период последовательности; U и τ – амплитуда и длительность каждого из радиоимпульсов соответственно; ω₀ – частота гармонического сигнала, заполняющего каждый из прямоугольных видеоимпульсов.

Спектр последовательности радиоимпульсов является линейчатым и представляет собой дискретную периодическую функцию, симметричную относительно частоты ω=ω₀.