Метод излучательности

В гл. 10 уже говорилось, что освещенность поверхности определяется собственным излучением тела и отраженными лучами, падающими от других тел (источников). Модель излучательности включает оба эти фактора и основана на уравнениях энергетического баланса. При этом выполняемые расчеты учитывают только взаимное расположение элементов сцены и не зависят от положения наблюдателя.

Представим сцену из N элементов (участков поверхностей). Освещенность будем моделировать как количество энергии, излучаемое поверхностью. Для каждого элемента это количество энергии складывается из собственной энергии ( ) и отраженной долей энергии, полученной от других объектов. Предполагается, что для каждой пары элементов с номерами можно определить, какая доля энергии одного попадает на другой ( ). Пусть — коэффициент отражения энергии ‑м элементом. Тогда полная энергия, излучаемая этим элементом, будет определяться уравнением

.

Таким образом, мы получаем систему уравнений для нахождения значений , которая в матричном виде выглядит следующим образом:

,

где — единичная матрица, и векторы излучаемой и собственной энергий, а матрица состоит из элементов . Поскольку часть излучения элемента может не попадать ни на один из оставшихся, то

,

а это условие в сочетании с тем, что (отражение не является полным) приводит к тому, что матрица системы имеет так называемое диагональное преобладание, т. е. диагональный элемент по абсолютной величине больше, чем сумма остальных элементов строки. В таком случае система уравнений имеет решение, которое можно найти с помощью численных методов.

Итак, шаги алгоритма изображения сцены сводятся к следующим:

1. Сцена разбивается на отдельные участки, для каждого из которых определяются значения

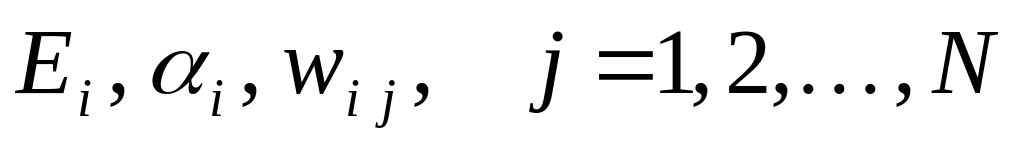
2. Находятся значения для каждой из трех основных компонент цвета.

3. Для выбранной точки наблюдения стоится проекция с удалением невидимых граней и осуществляется закрашивание, использующее значения для задания интенсивности. При этом могут использоваться какие-либо алгоритмы, позволяющие сгладить изображение.

Сложным моментом в модели излучательности является расчет коэффициентов .

Р

Рис. 10.2. Два элемента сцены

ассмотрим один пример. Пусть имеется два элемента сцены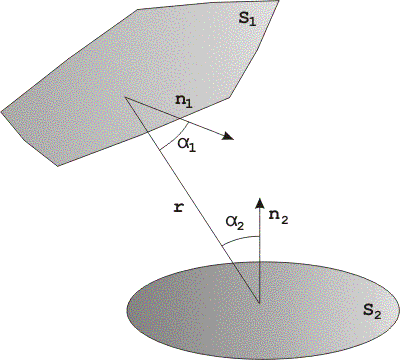 и (рис. 10.2). Поскольку используется диффузная модель освещения, то доля энергии малого участка с нормалью , излучаемая под углом к этой нормали, пропорциональна косинусу угла. Следовательно, в направлении элементарного участка уходит доля энергии, пропорциональная косинусу угла между и отрезком, соединяющим эти участки. Соответственно получаемая вторым участком доля этой энергии будет пропорциональна косинусу угла между нормалью и этим же отрезком. Итак, доля энергии, получаемая элементом от элемента где — расстояние между элементами. Кроме того, необходимо учесть, что излучаемая элементарным участком энергия равномерно распределена по всем направлениям. И, наконец, в каждой сцене одни объекты могут частично экранировать другие, поэтому надо ввести коэффициент, определяющий степень видимости объекта с позиции другого. Далее полученное выражение интегрируется по и , что также может быть сложной задачей.

Отсюда видно, насколько трудоемкой может оказаться процедура вычисления коэффициентов . Поэтому, как правило, используются приближенные методы их вычисления. В частности, можно рассматривать поверхности объектов как многогранники, тогда элементами сцены будут плоские многоугольники, для которых формулы несколько упрощаются.