Однородные координаты. Задание геометрических преобразований в однородных координатах с помощью матриц

В предыдущей главе описывались геометрические преобразования на плоскости и в пространстве, а также было показано, как можно использовать аппарат матриц для таких задач. Для преобразований на плоскости использовались двумерные векторы и матрицы размерностью 2х2. В пространстве, соответственно, с этой же целью использовались трехмерные векторы и матрицы 3х3. Но такой подход не позволяет задавать с помощью матриц преобразования переноса и проекции. В связи с этим в проективной геометрии был разработан аппарат, позволяющий унифицировать все геометрические преобразования путем введения так называемых однородных координат.

Для пояснения такого подхода сначала рассмотрим случай двумерного пространства. Каждая точка плоскости с координатами может одновременно рассматриваться как точка трехмерного пространства с координатами , т. е. как точка, лежащая на плоскости . С другой стороны каждой точке трехмерного пространства при условии соответствует единственная точка этой же плоскости . При этом получается, что каждой точке плоскости соответствует прямая, проходящая через начало координат, т. е. устанавливается взаимно однозначное соответствие между точками плоскости и множествами .

Если теперь рассматривать точку плоскости как принадлежащую трехмерному пространству, то ее двумерные преобразования можно будет описывать с помощью матриц 3х3, причем можно будет задавать таким способом не только повороты и масштабирование, но и сдвиги и проекции (как ортографические, так и центральные).

Поворот на угол относительно начала координат можно осуществить с помощью новой матрицы поворота:

.

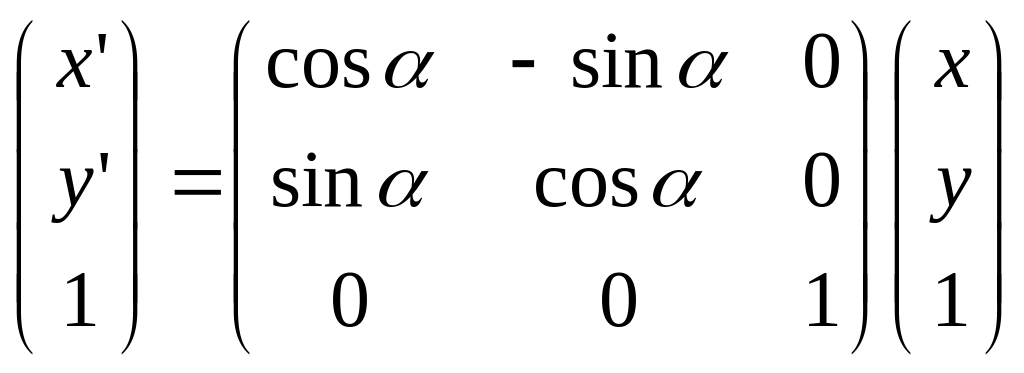Операция масштабирования может быть записана в виде

.

Перенос на вектор также можно задать с помощью матрицы:

.

Проекции точки на оси координат определяются с помощью матриц проектирования:

.

Перейдем теперь к трехмерному пространству. Каждой точке будем ставить в соответствие точку четырехмерного пространства , а для выполнения основных преобразований будем использовать матрицы размерностью 4х4. Строятся они совершенно аналогично тому, как это делалось в двумерном случае. Матрица сдвига на вектор имеет вид

,

матрица масштабирования тоже очевидным образом строится из трехмерной матрицы:

.

Проекции точек на координатные плоскости осуществляются с помощью матриц (более подробно проекции и их виды будут рассмотрены позднее):

.

Умножение этих матриц на вектор приводит к тому, что обнуляется одна из координат, и в результате получаем проекцию точки на соответствующую плоскость.

Матрица поворота, относительно оси на угол выглядит следующим образом

.

Отсюда легко понять, как строятся матрицы поворота относительно других координатных осей, а также матрица поворота относительно произвольной оси. Просто берем матрицы, построенные в третьей главе, и расширяем их путем добавления уже известных единичных вектора-строки и вектора-столбца:

.

Путем объединения приведенных элементарных преобразований можно построить и более сложные. В третьей главе мы использовали произведение простых матриц вращения для построения матрицы поворота относительно произвольной оси. Приведем один пример.

Пусть в пространстве заданы два отрезка и . Будем строить матрицу преобразования, переводящую первый отрезок во второй. Это преобразование разложим на следующие элементарные действия:

1. Сдвиг, перемещающий точку в точку .

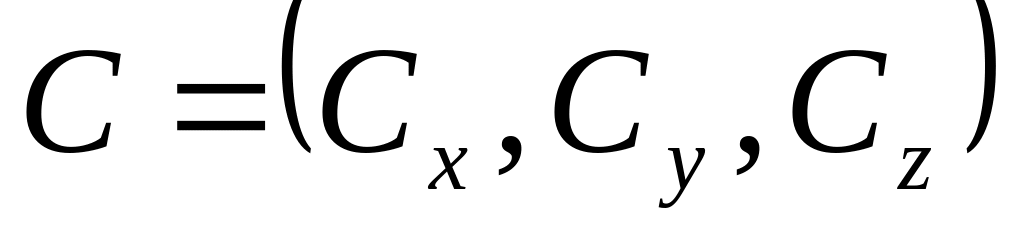2. Сдвиг начала координат в эту же точку

3. Если отрезки неколлинеарны:

— строится вектор нормали к плоскости, в которой лежат отрезки (для этого можно использовать векторное произведение исходных векторов);

— поворот относительно вектора нормали, совмещающий два отрезка по направлению (угол поворота можно определить с помощью скалярного произведения исходных векторов).

4. Масштабирование с целью выравнивания длины отрезков.

5. Возвращение начала координат в исходную точку.

Каждое из этих преобразований реализуется с помощью матрицы, а полное преобразование можно выполнить, используя произведение матриц.

Использование матриц очень удобно для выполнения преобразований в пространстве, хотя в некоторых случаях это приводит к избыточному числу выполняемых операций. Например, поворот одной точки в пространстве относительно координатной оси с помощью матриц в однородных координатах требует 16 операций умножения и 12 операций сложения. В то же время он легко может быть выполнен с помощью формул преобразования

,

т. е. с помощью всего лишь четырех умножений и одного сложения и одного вычитания. Операции сдвига также гораздо более экономично выполнять без использования матриц. Но когда речь идет о суперпозиции многих преобразований (как, например, в случае поворота относительно произвольной оси), то целесообразно использовать соответствующую матрицу поворота. Эффективность матричного подхода очень сильно возрастает, если матричные операции реализованы аппаратно. Вопрос о том, в каких случаях использовать матрицы, а в каких нет, во многом зависит от возможностей вычислительной техники, уровня сложности задачи и требований к временным характеристикам процесса визуализации.