Интерполяция функций одной и двух переменных

П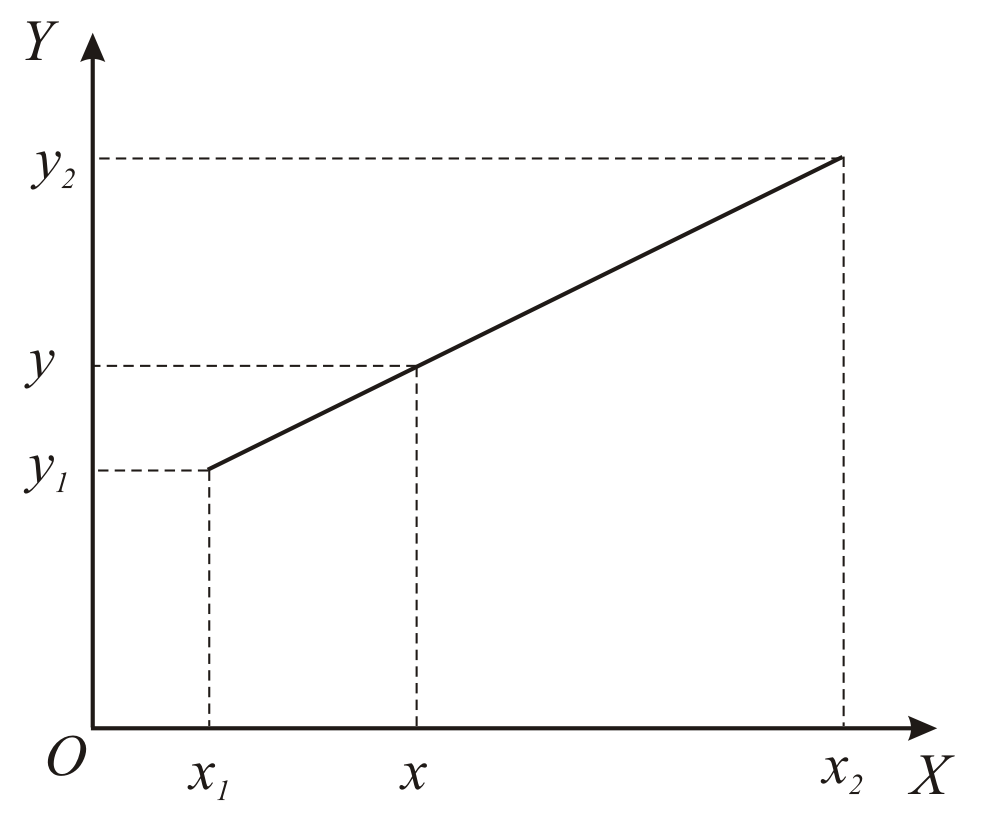 омимо функций, заданных аналитически (т. е. с помощью элементарных функций, значения которых легко могут быть вычислены в любой точке области определения) на практике часто приходится иметь дело с таблично заданными функциями. В этом случае функция задается своими значениями на некотором дискретном множестве точек (узлов)из области определения. Если необходимо получить значение функции в какой-либо точке, не совпадающей с узлом, используют различные методы приближенного вычисления, которые основываются на некоторых априорных предположениях относительно этой функции. При этом сама процедура вычисления называется интерполяцией в случае, когда точка принадлежит заданной области, и экстраполяцией, если она лежит вне области.

В

Рис. 3.3. Линейная интерполяция функции одной переменной

качестве предположений о характере дискретно заданной функции наиболее часто используемой и простой является то, что она кусочно-линейная, т. е. что в промежутках между узлами она ведет себя в соответствии с линейным законом. Тогда интерполяция называется линейной, и этот метод мы будем довольно часто применять в алгоритмах компьютерной графики.

Пусть на плоскости задана система координат и отрезок на оси , на концах которого заданы значения некоторой линейной функции (рис. 3). Тогда для любой точки внутри заданного отрезка соответствующее значение вычисляется по формуле

,

где

.

О

Рис. 3.4. Линейная интерполяция функции двух переменных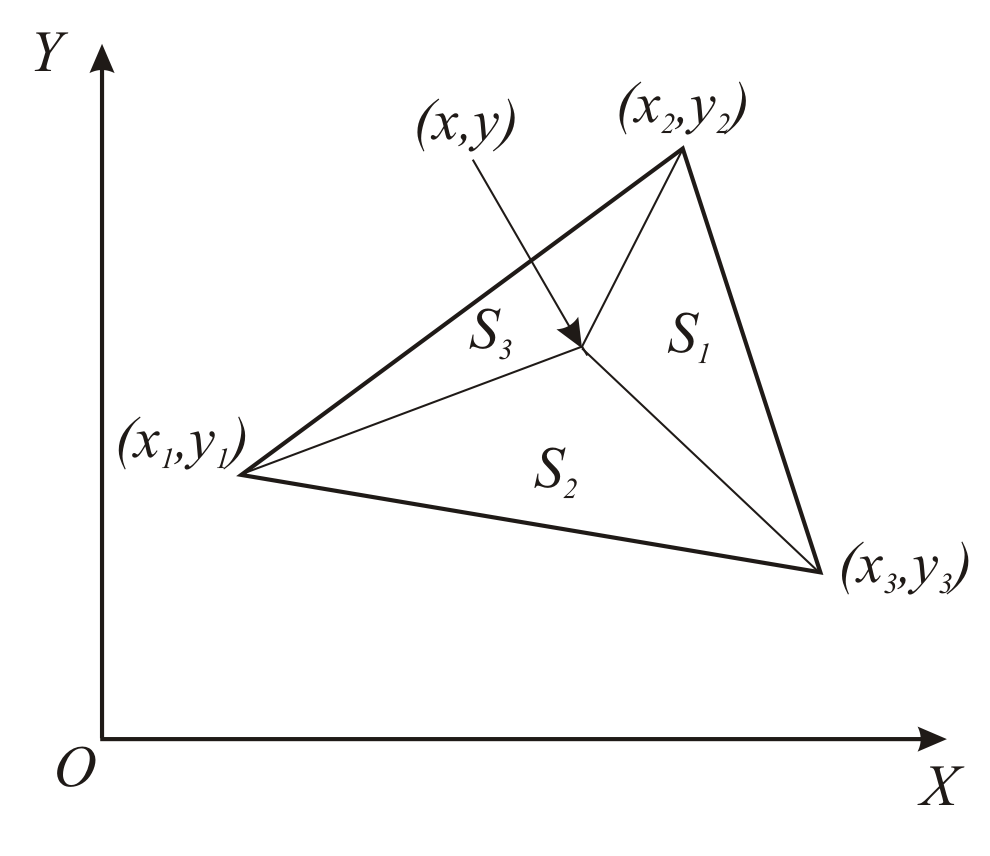

братимся теперь к задаче интерполяции функций двух переменных. В этом случае наиболее простой также является интерполяция по трем заданным точкам опять же с помощью кусочно-линейной функции. Пусть на плоскости задан треугольник с вершинами и заданы значения функции в этих точках . Тогда три точки определяют в пространстве треугольник, который является плоской фигурой. Предполагается, что площадь треугольника больше нуля, или, как говорят, треугольник невырожденный. Для определения значения функции в произвольной точке , лежащей внутри треугольника, воспользуемся так называемыми барицентрическими координатами этой точки. Геометрический смысл этих координат заключается в том, что они равны отношению площадей треугольников, изображенных на рис. 3.4:

Эти числа неотрицательны и удовлетворяют следующим соотношениям:

Эти соотношения будем рассматривать как уравнения для нахождения чисел .

Определитель этой системы уравнений есть

.

и он по модулю равен удвоенной площади треугольника, поэтому , и следовательно, система имеет единственное решение при любой правой части. Воспользуемся формулами Крамера и выпишем вид этого решения.

,

где

,

.

После того, как получены барицентрические координаты точки , значение функции в ней рассчитывается по формуле:

.

Существуют хорошо разработанные методы гладкой интерполяции функций. Особенно часто при интерполяции кривых и поверхностей используются сплайн-функции, которые гладко "склеиваются" из полиномов. Среди них следует выделить кубические сплайны, которые строятся из полиномов третьей степени. Они широко используются в инженерной геометрии благодаря простоте их вычисления и другим полезным свойствам. Мы их рассмотрим подробнее в последующих главах.