Оновной закон теплопроводности. Гипотеза фурье.

В случае стационарного температурного поля количество тепла, переданного в единицу времени путем теплопроводности через площадку, перпендикулярную grad t, можно описать простым соотношением, предложенным Фурье в 1822г.:

(1)

В практике теплотехнических расчетов широко пользуются понятием теплового потока:

(2)

Как уже говорилось, положительное значение grad t совпадает с направлением роста температуры. Между тем тепло, в соответствии со вторым началом термодинамики, самопроизвольно передается лишь в направлении убывания температуры. Эти два обстоятельства согласуются введением знака “минус” в правую часть уравнений (1) и (2).

Коэффициент λ, входящий в эти уравнения, носит название коэффициента теплопроводности. Уравнение (1) позволяет легко вскрыть физический смысл и единицы измерения λ:

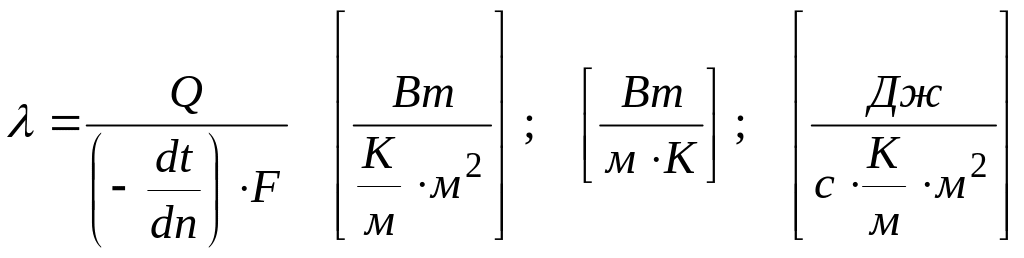
Коэффициент теплопроводности – теплофизическая характеристика вещества, характеризует способность вещества проводить теплоту.

Коэффициент теплопроводности – количество теплоты, проходящее в единицу времени через единичную площадку, перпендикулярную grad t, при значении последнего 1 .

Для различных веществ коэффициент теплопроводности λ различен и зависит от структуры, плотности, влажности, давления и температуры. Эти обстоятельства должны учитываться при использовании справочных таблиц.

Наибольшее значение имеет коэффициент теплопроводности металлов, для которых . Наиболее теплопроводным металлом является серебро , затем идут чистая медь , золото , алюминий и т.д. Для большинства металлов рост температуры приводит к уменьшению коэффициента теплопроводности. Эта зависимость в не слишком широком диапазоне температур может быть приближенно аппроксимирована уравнением прямой линии:

(3)

здесь λ и λ_о - соответственно коэффициенты теплопроводности при данной температуре t и при 0 ⁰С, β - температурный коэффициент (для металлов меньше нуля).

Коэффициент теплопроводности металлов очень чувствителен к примесям. Например, при появлении в меди даже следов мышьяка (Аs) ее коэффициент теплопроводности снижается с до ; для стали при 0,1% углерода , при 1,0% - , а при 1,5% углерода . Влияет на величину λ и термическая обработка. Так, у закаленной углеродистой стали λ на 10-25% ниже чем у мягкой. По этим причинам коэффициенты теплопроводности торговых образцов металла при одинаковых температурах могут существенно разниться. Следует отметить, что для сплавов, в отличие от чистых металлов, характерно увеличение коэффициент теплопроводности с ростом температуры. К сожалению, установить какие-либо общие количественные закономерности, которым подчиняется коэффициент теплопроводности сплавов пока не удалось.

Величина коэффициента теплопроводности строительных и теплоизоляционных материалов-диэлектриков во много раз меньше, чем у металлов и составляет 0,02-3,0 . Для подавляющего большинства из них (исключение составляет магнезитовый кирпич) с ростом температуры λ возрастает. При этом можно пользоваться уравнением (3), имея в виду, что для твердых тел-диэлектриков β >0.

Многие строительные и теплоизоляционные материалы имеют пористое строение (кирпич, бетон, асбест, шлак и др.). Для них и порошкообразных материалов коэффициент теплопроводности существенно зависит от объемной плотности. Это обусловлено тем, что с ростом пористости, большая часть объема заполняется воздухом, коэффициент теплопроводности которого очень низок. Вместе с тем, чем выше пористость, тем ниже объемная плотность материала. Таким образом, уменьшение объемной плотности материала, при прочих равных условиях, приводит к уменьшению λ. Например, для асбеста уменьшение объемной плотности с 800 кг/м³ до 400 кг/м³ приводит к уменьшению с 0,248 до 0,105 . Очень велико влияние влажности. Например, для сухого кирпича λ = 0,35 , для воды λ = 0,6, а для влажного кирпича .

На эти явления надо обращать внимание при определении и технических расчетах теплопроводности. Коэффициент теплопроводности капельных жидкостей лежит в пределах 0,08-0,7 . При этом для подавляющего большинства жидкостей с повышением температуры λ убывает. Исключение составляет вода и глицерин.

Коэффициент теплопроводности газов еще ниже ( ). Коэффициент теплопроводности газов растет с повышением температуры. В пределах от 20 мм.рт.ст. до 2000ат. (бар), т.е. в области, которая наиболее часто встречается на практике, λ от давления не зависит. Следует иметь в виду, что для смеси газов (дымовые газы, атмосфера термических печей и т.п.) расчетным путем определить λ невозможно. Поэтому при отсутствии справочных данных достоверная величина λ может быть найдена лишь опытным путем.

 < 1 – тепловые изоляторы.