Определение скорости потока на выходе из канала

Определение скорости потока можно осуществить путем интегрирования уравнения (1) в пределах от входного до выходного сечения канала.

Проинтегрируем уравнение (1)

или

. (11)

Решением интеграла в левой части уравнения (11) оказывается возможным, если известна зависимость . В общем случае можно признать, что изменение состояния газа в процессе течения происходит по закону политропы, т.е.

.

В случае адиабатного течения

. (12)

Подставляя значение v из (12) в (11) и производя интегрирование, получим

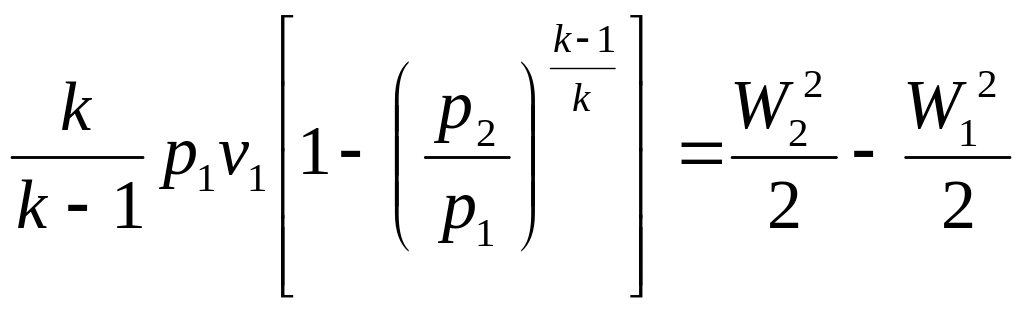. (13)

Уравнение (13) определяет приобретенный газом запас кинетической энергии, который может быть превращен в работу на колесе турбомашины. Поэтому величину, стоящую в левой части уравнения иначе называют располагаемой работой газового потока.

Располагаемая работа – это потенциальная энергия газа, которая может быть преобразована в кинетическую энергию потока при расширении его от давления р₁ до р₂.

Если принять , то из уравнения (13) следует, что скорость на выходе из канала будет равна

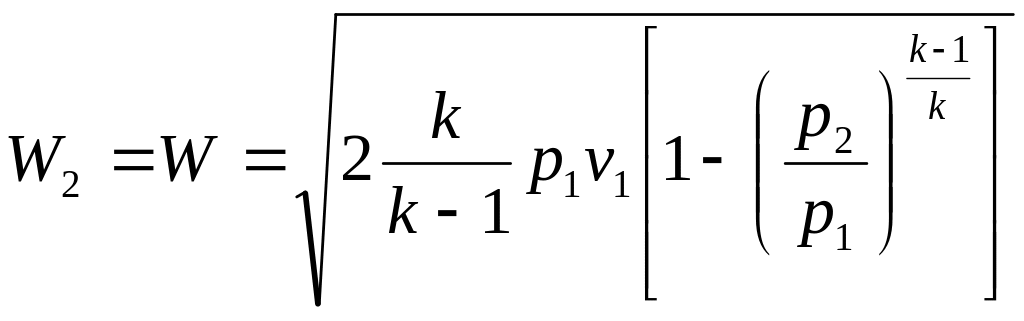. (14)

Массовый секундный расход газа

Массовый секундный расход газа может быть найден с помощью уравнения (2), в которое необходимо подставить площадь рассматриваемого поперечного сечения канала и соответствующие ему значения v и W.

Если , то W подсчитывается по уравнению (14), а удельный объем выражается через его значение в сечении 1-1. Тогда для случая адиабатного течения получим

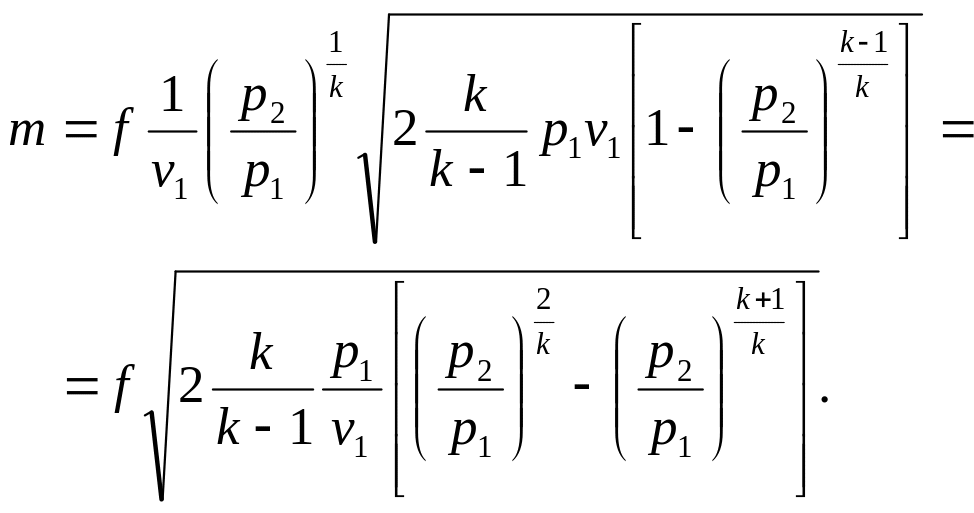(15)

Анализ соплового течения газа через суживающееся сопло

Анализ уравнения (15) позволяет перейти к выводу о том, что при заданных , и (область существования устойчивых равновесных состояний) величина массового секундного расхода зависит от значения выражения, взятого в квадратные скобки. Легко видеть, что при (рис. 2) . При расход газа за счет увеличения расширения газа на участке 1-1 2-2 растет. Однако, при m снова становится равным нулю. Поскольку функция (15), будучи непрерывной, дважды проходит через ноль, то должен существовать максимум массового секундного расхода (рис. 3).

Величина соотношения , отвечающая найдется, если взять первую производную от выражения в квадратных скобках уравнения (15) и приравнять ее нулю.

В результате получаем, что для адиабатного процесса изменения состояния критический перепад давлений равен

. (16)

Естественно, что при подстановке в уравнение (15) вместо критического перепада давлений мы получим максимальную величину массового секундного расхода. Например, для адиабатного течения, которое чаще всего рассматривается в технических приложениях, имеем

. (17)

При дальнейшем уменьшении давления, в окружающей среде 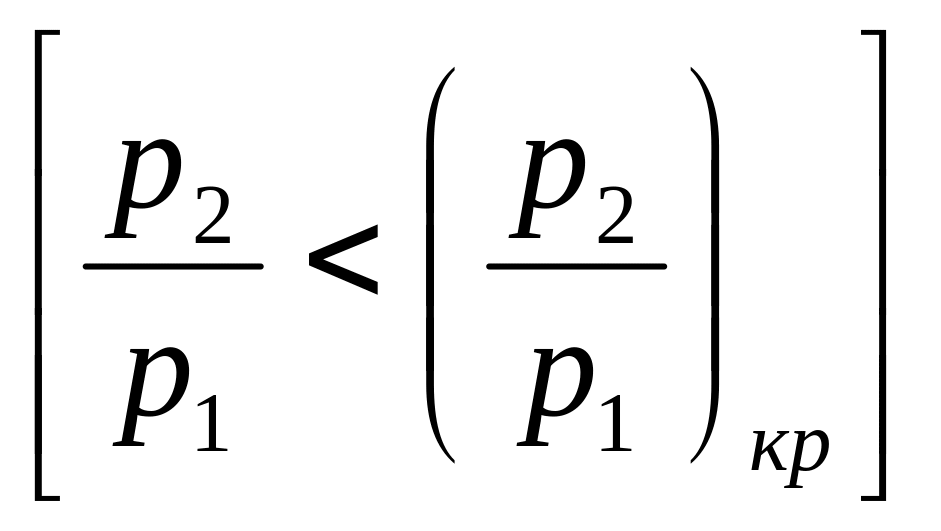расход остается постоянным, равным . Это явление получило название "кризис течения".

Скорость течения газа при также остается постоянной. Эта скорость называется критической скоростью течения . Уравнение для определения может быть получено, если в (14) вместо ввести критический перепад давлений

. (18)

Разберем физическую картину процесса. По мере движения газа по каналу происходит его расширение, при котором уменьшается и .

Снижение приводит к уменьшению местной скорости звука (9), а скорость потока возрастает. В выходном сечении канала скорость звука в соответствии с (9) будет равна

. (19)

При кризисе течения скорость потока в выходном сечении определяется (18). Введем в это уравнение вместо температуру Т. Для адиабатного процесса при

или

.

Таким образом, при достижении критического перепада давлений на выходе из суживающегося сопла скорость потока достигает местной скорости звука. Между тем, давление распространяется тоже со скоростью звука. В результате, уменьшение в окружающей среде давления ниже не может подойти к устью сопла, и в последнем устанавливается постоянное давление, равное (19). Этим объясняется тот факт, что при

и

.