Обратная задача оценки постоянного срочного аннуитета постнумерандо.

В этом случае производится оценка будущих денежных поступлений с позиции текущего момента, под которым понимается момент времени, начиная с которого отсчитываются равные временные интервалы, входящие в аннуитет.

Общая формула для оценки текущей стоимости срочного аннуитета постнумерандо выводится из ранее выведенной основной формулы и имеет вид:

Множитель называется коэффициентом дисконтирования ренты и как сумма членов геометрической прогрессии равен величине:

.

Экономический смысл дисконтного множителя заключается в следующем: он показывает, чему равна с позиции текущего момента стоимость аннуитета с регулярным денежным поступлением в размере одной денежной единицы, продолжающегося n равных периодов с заданной процентной ставкой r. Значения этого множителя табулированы в финансовых таблицах.

Дисконтный множитель можно интерпретировать и как величину капитала, поместив который в банк под сложную процентную ставку r, можно обеспечить регулярные выплаты в размере одной денежной единицы в течение n периодов.

Из ранее выведенной формулы для определения множителя следует, что при возрастании процентной ставки величина множителя уменьшается и, таким образом, уменьшается величина приведенной стоимости.

В случае рассмотрения только сложных процентов формулы для нахождения приведенных стоимостей аннуитетов аналогичны формулам для нахождения наращенных сумм. Получающиеся при этом денежные потоки будут представлять собой геометрические прогрессии, знаменателями которых будут соответствующие дисконтные множители.

Так, для постоянного аннуитета постнумерандо с начислением сложных процентов m раз за базовый период приведенный денежный поток имеет вид:

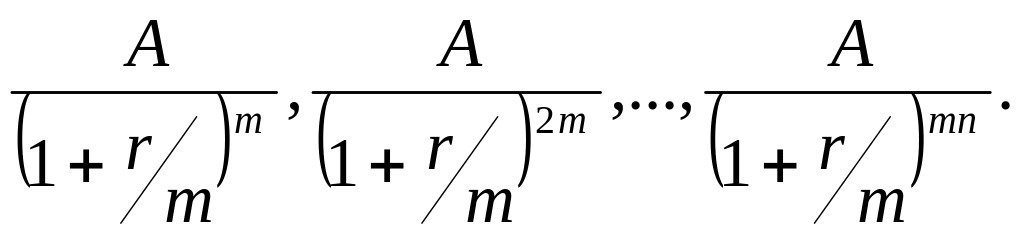
Следовательно, приведенная стоимость такого аннуитета будет равна:

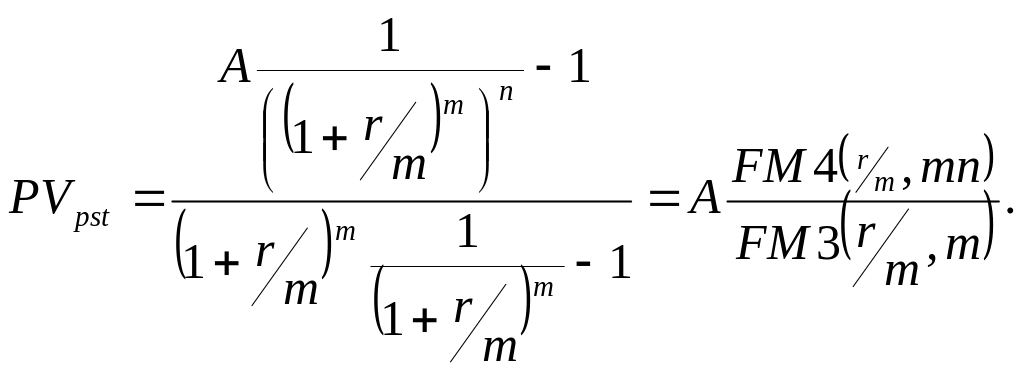
Для р-срочных аннуитетов с начислением сложных процентов соответственно один раз за базовый период и m раз за базовый период аналогичным образом можем получить следующие формулы для определения приведенной стоимости:

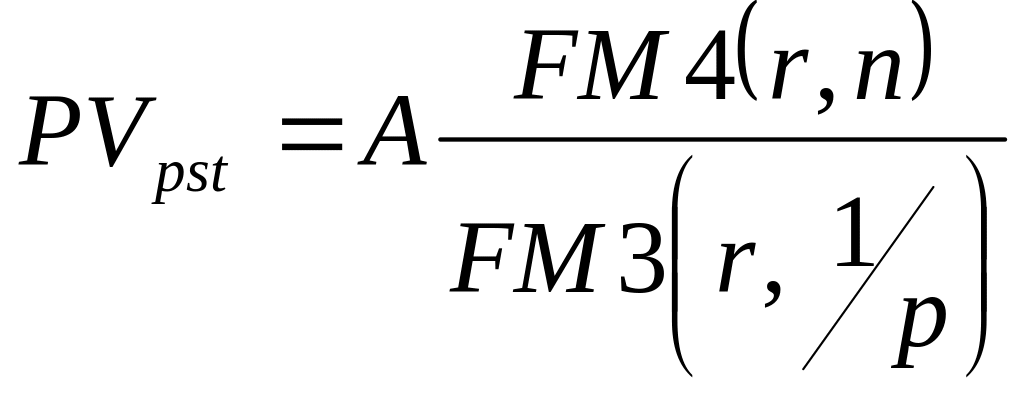
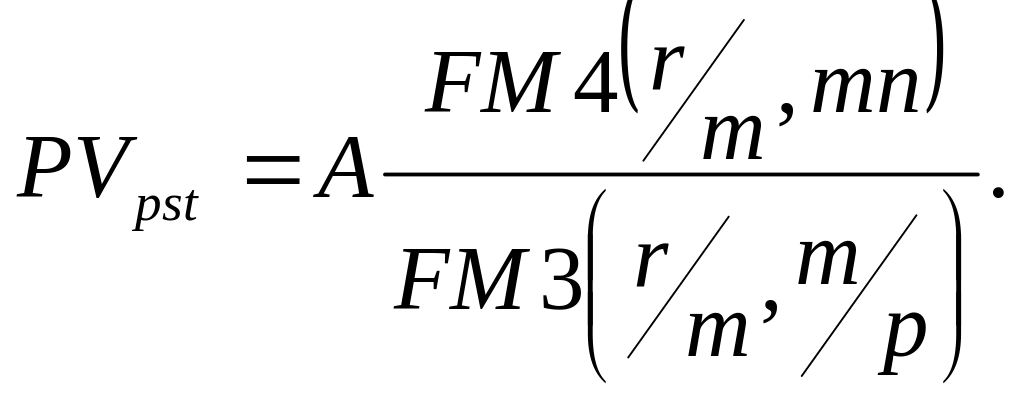
Пример.

Страховая компания, заключив на 4 года договор с некоторой фирмой, получает от нее страховые взносы по 20 тыс. грн. в конце каждого полугодия. Эти взносы компания помещает в банк под 12% годовых.

Необходимо найти приведенную стоимость суммы, которую получит страховая компания по данному контракту, если проценты будут начисляться: а) раз в полгода; б) ежемесячно.

а) полугодовое начисление процентов:

n = 4, r = 12%, m = 2, p = 2.

тыс. грн.

б) ежемесячное начисление процентов:

n = 4, r = 12%, m = 12, p = 2.

тыс. грн.

Отсроченный аннуитет постнумерандо.

В практике финансовых операций имеют место соглашения, когда первый из потока платежей начинает поступать не сразу, а через h периодов.

Предположим, что платежи поступают в течение периодов и сложные проценты по ставке начисляются один раз в конце базового периода, совпадающего с периодом аннуитета.

Стоимость этого аннуитета на начало периода, когда поступает первый платеж, находится по формуле и затем, осуществляя учет полученной величины за периодов, определяем приведенную стоимость отсроченного аннуитета на начальный момент времени.

Для этой цели используется следующая формула:

Из приведенной формулы видно, что приведенная стоимость отсроченного аннуитета представляет собой разность приведенных стоимостей аннуитетов с платежами, начиная с первого периода.

Пример.

Банк предлагает ренту постнумерандо на 10 лет с ежеквартальной выплатой 100 грн. Годовая процентная ставка в течение всего периода остается постоянной. По какой цене можно приобрести такую ренту, если выплаты начнут осуществляться: а) немедленно; б) через 2 года; в) через 3,5 года, а процентная ставка равна 2, 4, 12% годовых.

а) вариант немедленного начала выплат.

n = 10*4 = 40, r = 2%:4 = 0,5%.

грн.

б) вариант начала выплат через 2 года.

N = 40, r = 4% : 4 = 1%, h = 2*4 = 8.

грн.

в) вариант начала выплат через 3,5 года.

n = 40, r = 12% : 4 = 3%, h = 3,5 *4 = 14.

грн.

Из рассмотренного примера видно, что с ростом процентной ставки и срока, после которого начнутся выплаты, приведенная стоимость аннуитета уменьшается. Так, если выплаты начнутся через 3,5 года и процентная ставка составит 12% годовых, то указанную ренту можно приобретать за 1528,15 грн. или, естественно, дешевле. В то же время приведенная стоимость ренты с отсрочкой выплаты на 2 года и при процентной ставке 4% годовых составляет вдвое больше – 3032,23 грн.

Как следует из формулы для определения будущей стоимости аннуитета постнумерандо в самом общем виде

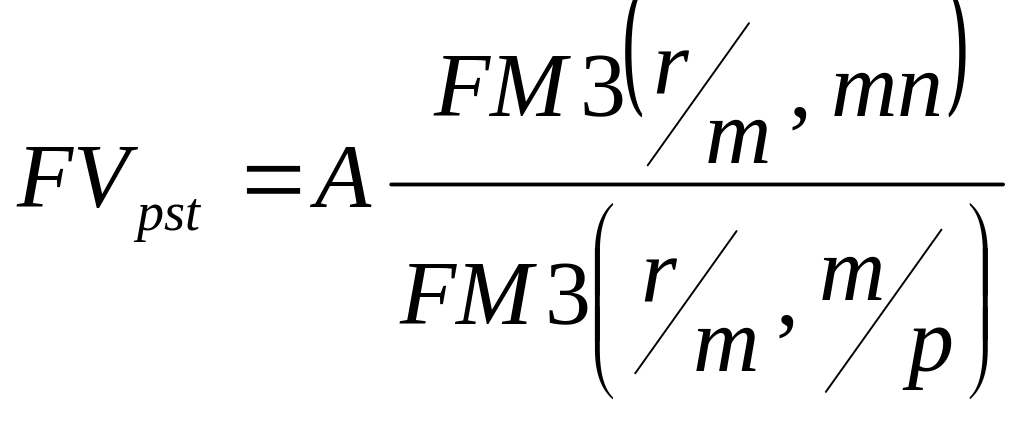
для нахождения будущей стоимости необходимо, чтобы были заданы значения следующих параметров: A, r, n, m, p. Однако, при заключении некоторого контракта уже заранее может быть задана будущая стоимость аннуитета, а необходимо определить, например, величину разовых денежных поступлений А. В этом случае при заданных значениях остальных параметров, величина разового денежного поступления может быть определена по формуле:

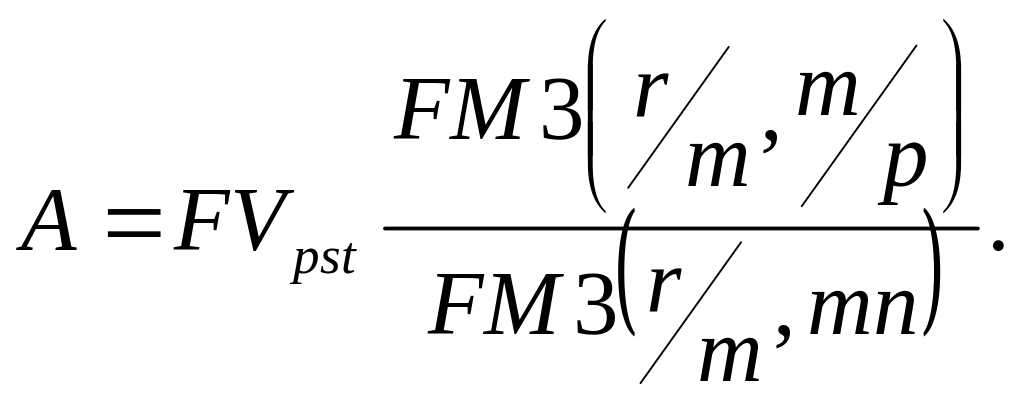
Если известна приведенная стоимость и остальные параметры, а необходимо найти величину разового платежа, то используется формула:

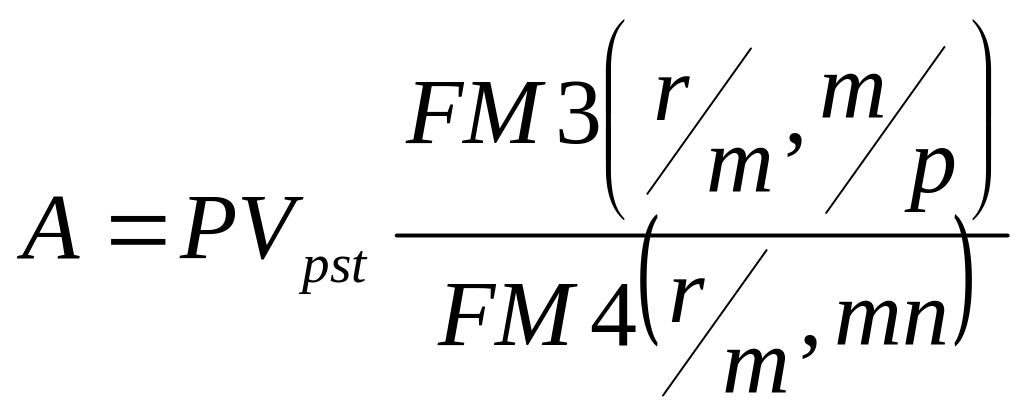
Величину разового платежа можно определить иначе. Мы помним, что Значит, , откуда с помощью несложных преобразований, получим:

Аналогичным образом можно получить формулу для определения величины разового платежа (или поступления), если имеет место аннуитет постнумерандо и задана его приведенная стоимость. В этом случае формула имеет вид:

Пример.

Работник заключает с фирмой контракт, согласно которому в случае его постоянной работы на фирме до выхода на пенсию в 65 лет фирма обязуется перечислять в конце каждого года в течение 20 лет на счет работника в банке одинаковые суммы, которые обеспечат работнику после выхода на пенсию ежегодные дополнительные выплаты в 6000 тыс. грн. в течение 15 лет.

Какую сумму каждый год должна перечислять фирма, если работнику 45 лет и предполагается, что банк гарантирует годовую процентную ставку 10% годовых?

грн.

грн.

Зачастую при заключении финансовых контрактов имеют место случаи, когда заданы все остальные параметры, а необходимо определить срок действия аннуитета. В этом случае исходим из базовой формулы будущей стоимости аннуитета:

Из этой формулы путем несложных преобразований получим:

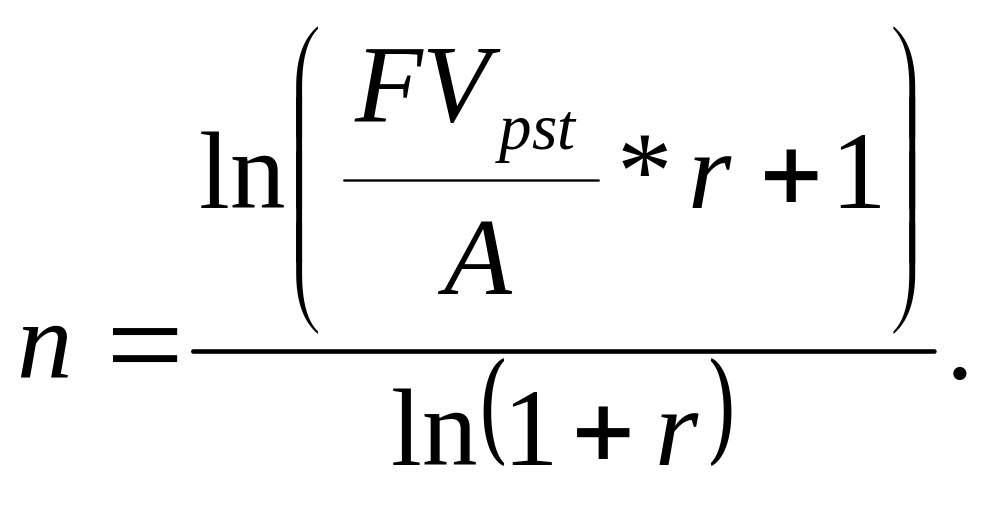
Если решается обратная задача оценки срочного аннуитета постнумерандо и необходимо определить срок действия такого аннуитета, то в этом случае применяется формула:

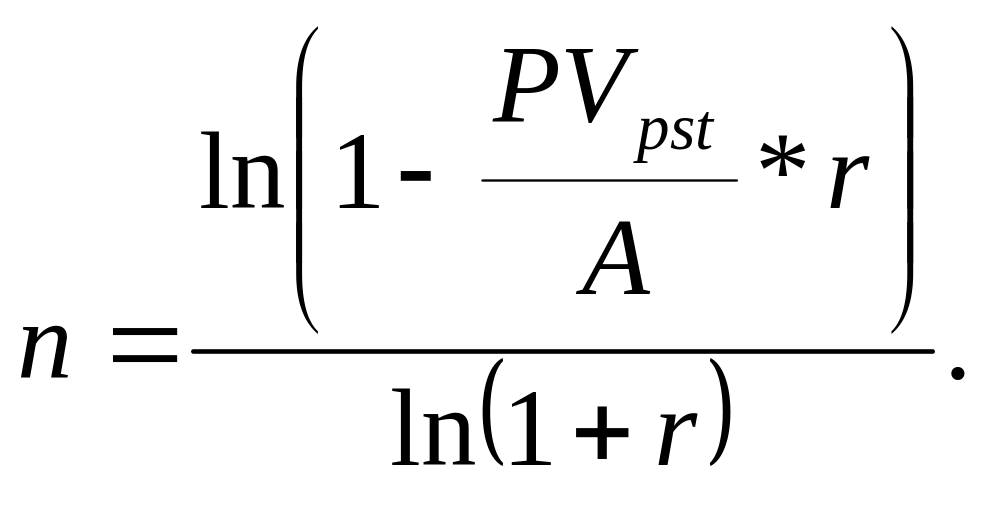
Пример.

Предприятие хочет создать фонд в размере 200 тыс. грн. С этой целью в конце каждого года предприятие предполагает втосить по 50 тыс. грн. в банк под 18% годовых.

Найти срок, необходимый для создания фонда.

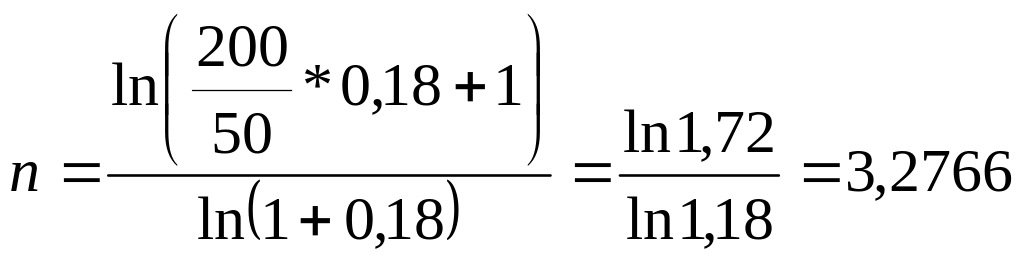года

Если известны все параметры аннуитета кроме величины процентной ставки, то в этом случае используется метод линейной интерполяции, так как непосредственно из ранее приведенных формул величину процентной ставки определить нельзя.

Рассмотрим метод линейной интерполяции на конкретном примере.

Пример.

В течение 4-х лет предполагается создать резервный фонд в размере 20 тыс. грн., для чего будут производиться ежегодные взносы в банк в размере 4 тыс. грн.

Необходимо определить размер процентной ставки при условии, что взносы и начисление на них процентов производится в конце года.

Прежде всего определим коэффициент наращения ренты, который равняется : .

По финансовым таблицам находим ближайшие значения факторного множителя: и .

Для расчета процентной ставки по методу линейной интерполяции используется формула:

где нижнее и верхнее значение предполагаемой процентной

ставки;

значения коэффициентов наращения при использовании процентных ставок и .

Для условий нашего примера значение процентной ставки, обеспечивающей за указанный срок создание резервного фонда в заданном объеме рассчитывается по формуле:

или 15,09%.

Оценка постоянного аннуитета пренумерандо.

Если на денежные поступления начисляются только сложные проценты, то соответствующие расчетные формулы для наращенных сумм аннуитета пренумерандо легко можно вывести из ранее рассмотренных формул для аннуитета постнумерандо.

Поскольку денежные поступления в аннуитете пренумерандо происходят в начале каждого периода, то этот аннуитет отличается от аннуитета постнумерандо только количеством периодов начисления процентов.

Например, для срочного аннуитета пренумерандо с регулярными денежными поступлениями А и процентной ставкой r , наращенный денежный поток имеет вид:

Следовательно, будущая стоимость аннуитета пренумерандо может быть определена по формуле:

Т.е. наращенная стоимость аннуитета пренумерандо больше в раз наращенной суммы аннуитета постнумерандо.

Аналогичным образом можно получить формулы для определения будущей стоимости аннуитета пренумерандо с начислением процентов m раз в течение базового периода и для р-срочных аннуитетов:

Несколько иной будет ситуация в р-срочном аннуитете пренумерандо, когда на взносы, поступающие в течение базового периода, начисляются простые проценты.

В отличие от аннуитета постнумерандо в этом аннуитете в каждом периоде любой взнос «действует» еще 1/р –ю часть периода, тем самым доставляя к концу периода дополнительную величину .

Следовательно, к концу каждого периода взносы, число которых равно р , доставят величину

Таким образом, на последнее р-е поступление начисляются простые проценты за часть периода, равную 1/р , и оно будет равно предпоследнее (р – 1)-е поступление станет равным и т.д. вплоть до первого поступления, которое станет равным . Следовательно, сумма этих величин, образующих арифметическую прогрессию, равна:

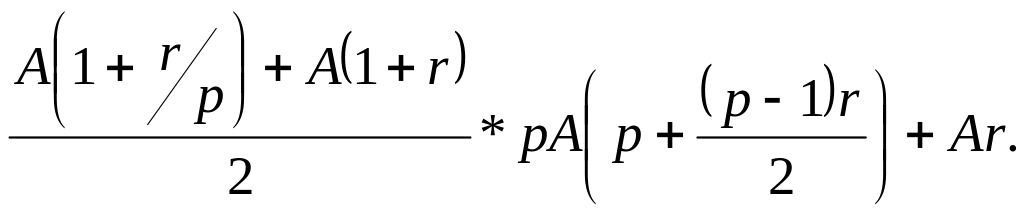
Таким образом, будущая стоимость аннуитета пренумерандо будет равняться:

В случае начисления только сложных процентов формулы для расчетов приведенных стоимостей пренумерандо имеют вид, аналогичный ранее полученным для аннуитета постнумерандо:

Из приведенных формул понятно, почему в финансовых таблицах не уточняется, какая схема подразумевается в финансовой сделке – постнумерандо или пренумерандо. Содержание таблиц инвариантно к этому фактору. Однако, при применении расчетных формул или финансовых таблиц необходимо строго следить за схемой поступления денежных платежей.

Пример.

Ежегодно в начале года в банк делается очередной взнос в размере 10 тыс. грн. Банк платит 20% годовых.

Какая сумма будет на счете по истечении трех лет?

тыс. грн.

Многие практические задачи могут быть решены различными способами в зависимости от того, какой денежный поток выделен аналитиком. Рассмотрим это на следующем примере.

Пример.

Вам предложено инвестировать 100 тыс. грн. на срок 5 лет при условии возврата этой суммы частями ежегодно по 20 тыс. грн. По истечении 5 лет выплачивается дополнительное вознаграждение в размере 30 тыс. грн.

Следует ли принимать это предложение, если можно депонировать деньги в банк из расчета 12% годовых?

Наращенная сумма депонирования:

тыс. грн.

В отношении альтернативного варианта, предусматривающего возмещение вложенной суммы частями, предполагается, что ежегодные поступления в размере 20 тыс. грн. можно немедленно пускать в оборот, получая дополнительные доходы. Если нет других альтернатив по эффективному использованию этих сумм, их можно депонировать в банк. В этом случае денежный поток можно представить двояко:

а) как срочный аннуитет постнумерандо с параметрами: А= 20,

n = 5, r = 20% и единовременное получение 30 тыс. грн. в конце периода:

тыс. грн.

б) как срочный аннуитет пренумерандо с параметрами: А = 20,

n = 4, r = 20% и единовременное получение сумм в 30 и 20 тыс. грн. в конце финансовой операции:

тыс. грн.

Таким образом, предложение экономически нецелесообразно.

Бессрочный аннуитет.

Аннуитет считается бессрочным, если денежные поступления продолжаются достаточно длительное время. Математически это означает, что . Характерным примером бессрочного аннуитета являются консоли – выпускаемые правительствами некоторых стран облигации, по которым производят регулярные купонные выплаты, но которые не имеют фиксированного срока. В западной практике к бессрочным относятся аннуитеты, рассчитанные на 50 и более лет. Бессрочный аннуитет также называют вечной рентой.

Определение будущей стоимости бессрочного аннуитета, естественно, не имеет смысла. Что же касается обратной задачи (определение приведенной стоимости), то она имеет вполне определенное решение.

Поток платежей в постоянном бессрочном аннитете при одном денежном поступлении А за период, являющися базовым для начисления процентов по ставке r, представляет собой бесконечно убывающую геометрическую прогрессию с первым членом и знаменателем . Для бессрочного аннуитета постнумерандо формула для определения приведенной стоимости имеет вид:

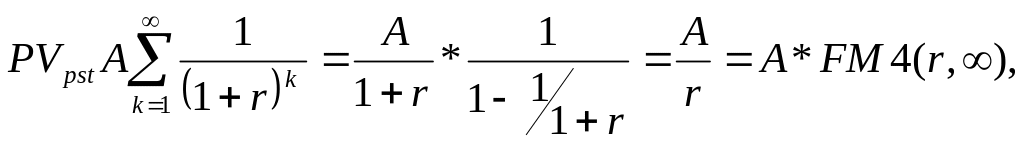
где

Приведенная формула показывает, что поток даже с неограниченным числом платежей имеет все же конечную приведенную стоимость. С финансовой точки зрения это вполне понятно, поскольку деньги, которые поступят через много лет, сейчас мало что стоят, а при высокой инфляции и ничего не стоят. Эта же ситуация проявляется и при сравнении коэффициентов дисконтирования бессрочного аннуитета и аннуитетов с большим сроком Для сравнения приведем в таблице значения FM4(r,n) при r = 10%.

Cрок аннуитета	40	50	60	70	90	∞
FM4(r = 10%,n)	9,7791	9,9148	9,9672	9,9873	9,9981	10

Из приведенной таблицы видно, что при сроке аннуитета, превышающем 50 лет, коэффициенты дисконтирования аннуитета незначительно отличаются друг от друга.

Кроме того, с ростом процентной ставки величина срока, начиная с которого величина факторного множителя FM4(r,n) перестают сильно отличаться друг от друга, уменьшается. Например, при r = 15% такой срок равняется 40 годам. Таким образом, при больших сроках аннуитета и большом уровне процентной ставки для определения приведенной стоимости срочного аннуитета можно воспользоваться формулой для определения приведенной стоимости бессрочного аннуитета, при этом полученный приблизительный результат будет не слишком отличаться от точного значения.

Приведенная формула используется для оценки целесообразности приобретения бессрочного аннуитета, если известен размер денежного поступления за период. В качестве r обычно принимается гарантированная процентная ставка, например, предлагаемая государственным банком.

Пример.

Необходимо определить текущую стоимость бессрочного аннуитета постнумерандо с ежегодным поступлением 4,2 тыс. грн., если предлагаемый государственным банком процент по срочным вкладам равен 14% годовых.

тыс. грн.

Следовательно, если аннуитет предлагается по цене, не превышающей 30 тыс. грн., то инвестирование в него будет представлять выгодную для инвестора операцию.

С помощью вышеприведенной формулы можно определить истинную стоимость обыкновенной акции в том случае, когда выплачиваются одинаковые дивиденды (равные А) в течение всего времени финансовой операции. При этом предположении темп ростов дивидендов равен нулю и соответствующая модель называется моделью нулевого роста.

Такая ситуация в определенном смысле свойственна привилегированным акциям высокого качества, выплаты дивидендов по которым одинаковы, регулярны и не зависят от величины прибыли на одну акцию, а время обращения привилегированных акций не ограничено.

Пример.

Компания гарантирует выплату дивидендов в размере 6 тыс. грн. на акцию в конце каждого года в течение неопределенно долгого времени.

Имеет ли смысл покупать акции этой компании в течение неопределенно долгого времени по цене 35 тыс. грн., если можно поместить деньги на депозит под 15% годовых?

Из формулы тыс. грн. следует, что истинная стоимость акции составляет 40 тыс. грн. Следовательно, это предложение может быть принято и акции компании можно приобретать.

Приведенная стоимость бессрочного аннуитета постнумерандо с денежными поступлениями р раз за базовый период и начислением сложных процентов m - раз за период может быть получена из следующей формулы:

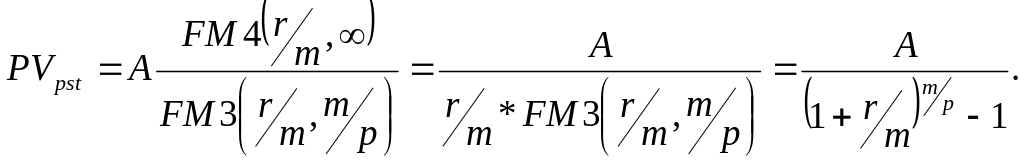
Пример.

Фирма собирается учредить фонд для ежегодной (в конце года) выплаты пособий своим работникам.

Необходимо определить сумму, которую фирма должна поместить на депозит в банк, чтобы обеспечить получение неограниченно долго в конце каждого года 8 тыс. грн., если банк начисляет:

а) ежегодно сложные проценты по ставке 16%;

б) ежеквартально сложные проценты по ставке 14%;

в) непрерывные проценты с силой роста 13,5%.

Во всех трех случаях денежный поток является бессрочным аннуитетом постнумерандо. Необходимо найти приведенную стоимость такого аннуитета.

а) тыс. грн.

б) 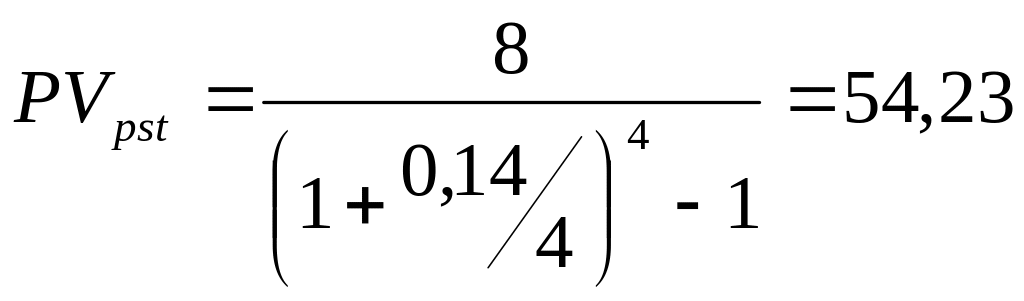тыс. грн.

в) тыс. грн.

Приведенная стоимость бессрочного аннуитета пренумерандо в общем виде определяется с помощью приведенной стоимости бессрочного аннуитета постнумерандо по следующей формуле:

Следовательно, приведенная стоимость бессрочного аннуитета пренумерандо отличается от таковой для аннуитета постнумерандо на величину первого платежа.

Непрерывный аннуитет.

Предположим, что в течение каждого периода времени денежные поступления происходят очень часто, так что промежутки между последовательными поступлениями представляют собой бесконечно малые величины.

В этом случае аннуитет считают непрерывным, т.е. денежные поступления происходят непрерывно с постоянной интенсивностью: одно и то же количество денежных единиц в единицу времени.

Соотношения, характеризующие непрерывный аннуитет, можно вывести из формул для р-срочного аннуитета, переходя в них к пределу при и несколько модифицируя величину члена аннуитета.

Ясно, что непрерывно не может поступать величина А, так как через любой малый промежуток времени накопится бесконечно большая сумма денег.

Пусть в конце каждого периода р-срочного аннуитета суммарная величина денежных поступлений составит , тогда каждое поступление будет равняться и ранее рассмотренная формула 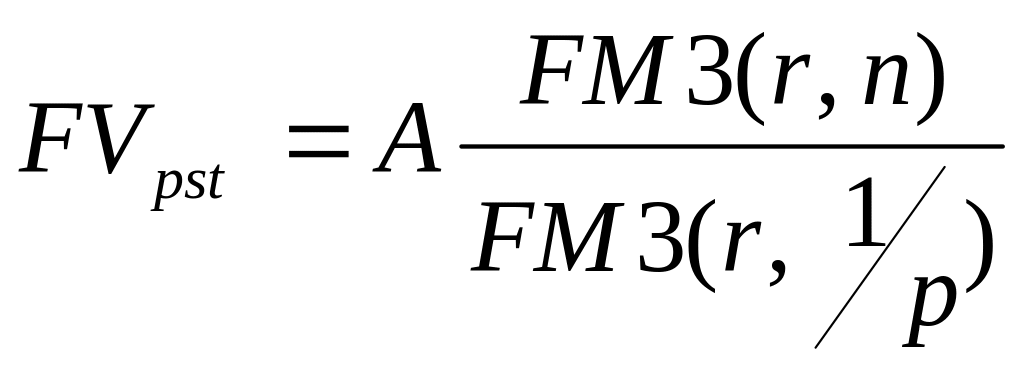может быть использована для оценки будущей стоимости непрерывного аннуитета:

Приведенная стоимость непрерывного аннуитета рассчитывается по формуле:

Пример.

В течение 6 лет на счет в банке ежедневно будут поступать одинаковые платежи, каждый год составляя 40 тыс. грн.

Определить сумму, накопленную к концу шестого года при использовании процентной ставки 12% годовых.

Считая, что платежи поступают непрерывным образом, рассчитаем будущую стоимость непрерывного аннуитета:

тыс. грн.

Эта же задача может быть решена иначе, если примем р = 360, а А = 40/360:

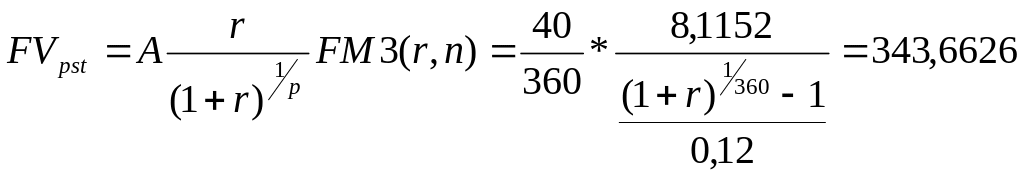тыс. грн.

Выполнив расчет видим, что результаты вычислений по двум формулам привели практически к одинаковому результату.

Если проценты начисляются раз за период, то пользуются формулой:

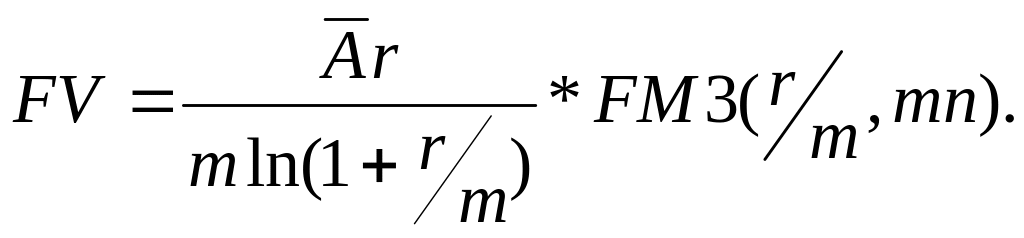
Аннуитет с изменяющейся величиной платежа.

На практике возможны ситуации, когда величина платежа меняется со временем в сторону увеличения или уменьшения. Например, при заключении договора аренды в условиях инфляции может предусматриваться периодическое увеличение платежа, компенсирующее негативное влияние изменения цен. Или другой пример, когда величина амортизационных отчислений может меняться в связи с изменением количества и стоимости основных фондов.

В таких ситуациях поток платежей представляет собой переменный аннуитет (переменную ренту) и для определения будущей или приведенной стоимости необходимо пользоваться ранее рассмотренными формулами для переменного аннуитета. Однако, когда члены аннуитета изменяются в соответствии с некоторыми законами, эти формулы существенно могут быть упрощены.

Предположим, что имеется аннуитет постнумерандо, платежи которого образуют арифметическую прогрессию с первым членом А и разностью z.

В этом случае говорят о переменном аннуитете с постоянным абсолютным изменением его членов. Если число периодов равно n, а r является процентной ставкой за базовый период, в соответствии с которой один раз в конце периода начисляются сложные проценты и период аннуитета совпадает с базовым, то наращенный денежный поток, записанный в порядке поступления платежей имеет вид:

Если z >0, то члены аннуитета возрастают. Если z <0, члены аннуитета убывают и число этих членов должно удовлетворять равенству n < 1 – A/z, иначе можно получить отрицательные платежи, что лишено смысла.

Сложив наращенные члены аннуитета и сгруппировав отдельно слагаемые, содержащие множители А и z, получим:

Из этого выражения с помощью определенных преобразований получаем формулы для определения будущей и приведенной стоимости такого аннуитета:

Пример.

Согласно условиям финансового соглашения на счет в банке в течение 6 лет в конце года будут поступать денежные суммы, первая из которых равна 5 тыс. грн., а каждая последующая будет увеличиваться на 0,4 тыс. грн.

Необходимо оценить аннуитет, если банк применяет процентную ставку 10% годовых и сложные проценты начисляются один раз в конце года.

Как изменятся оценки аннуитета, если денежные суммы будут уменьшаться на 0,4 тыс. грн.?

а) для условия возрастания членов аннуитета:

тыс.грн.

тыс. грн.

б) для условия уменьшения членов аннуитета:

тыс. грн.

тыс. грн.

Для оценки аннуитетов пренумерандо используются следующие формулы:

Аналогичным образом можно получить оценки аннуитета для других ситуаций, например, для случая, если в указанных выше условиях начисление сложных процентов происходит раз за базовый период:

Пример.

В условиях предыдущего примера определить будущую стоимость аннуитета, если начисление сложных процентов происходит в конце каждого полугодия.

тыс.грн.

Из формул для определения будущей и приведенной стоимости аннуитета можно определить величину аннуитета А и разность z:

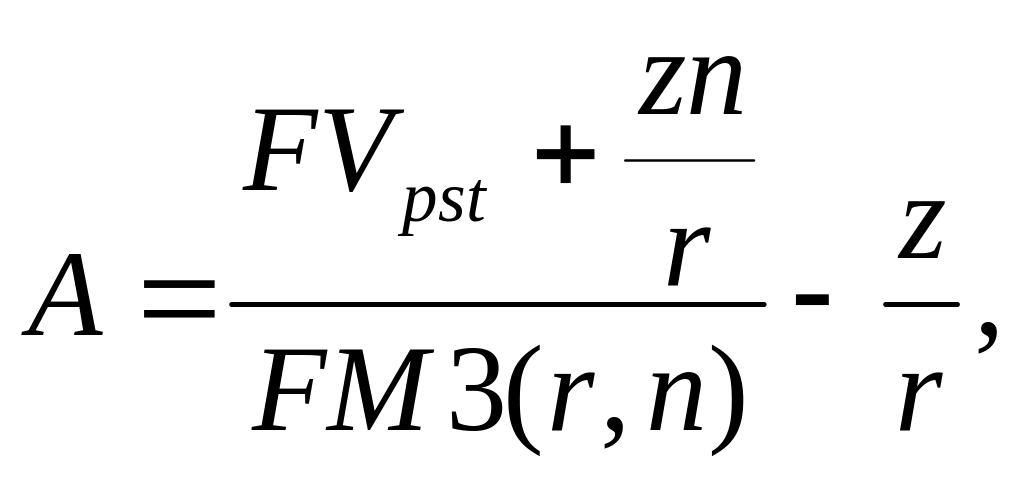
Что касается процентной ставки и продолжительности аннуитета, то формулы для их определения в явном виде не могут быть получены. Поэтому для определения этих параметров используются приближенные методы.

Пример.

За 10 лет необходимо накопить 60 тыс. грн. Какой величины должен быть первый вклад, если предполагается каждый год увеличивать величину денежного поступления на 300 грн. и процентная ставка равна 15% годовых? Денежные поступления и начисление сложных процентов осуществляются в конце года.

Определить, на какую величину необходимо увеличивать каждый год денежное поступление, если первый вклад будет равен 2,5 тыс. грн.?

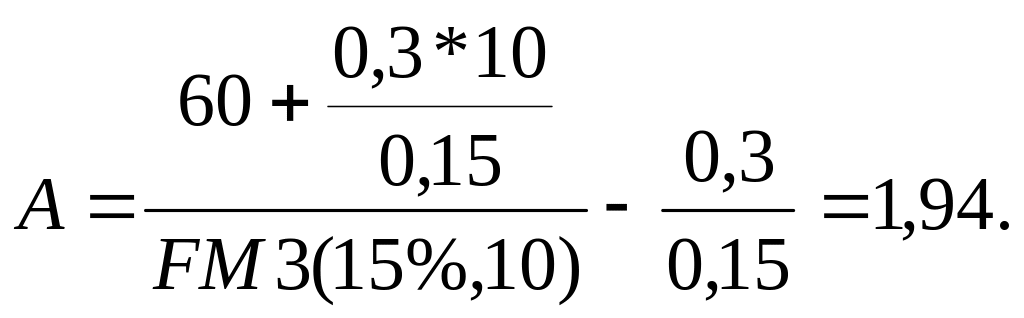тыс.грн.

тыс. грн.

Предположим, что платежи в аннуитете образуют геометрическую прогрессию с первым членом А и знаменателем q.

В этом случае имеет место переменный аннуитет с постоянным относительным изменением его членов.

Если r является процентной ставкой за базовый периолд, совпадающий с периодом аннуитета, n равно числу периодов и в конце каждого периода начисляются сложные проценты, то наращенный денежный поток имеет вид:

Представленная последовательность чисел представляет собой геометрическую прогрессию с первым членом и знаменателем . Поэтому будущая стоимость такого аннуитета будет равна:

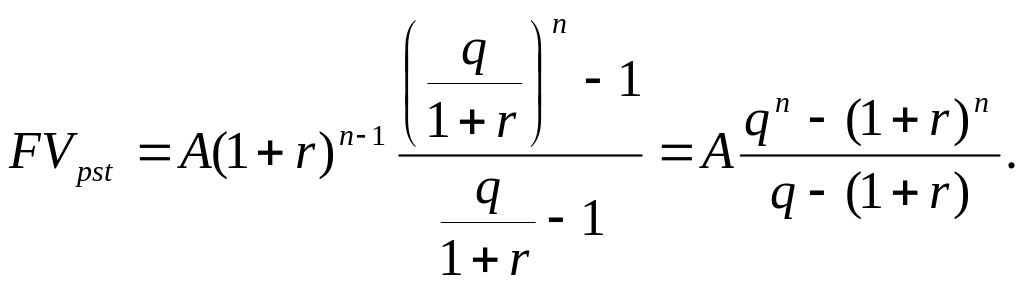
Приведенная стоимость аннуитета определяется по формуле:

Пример.

По условиям контракта на счет в банке поступают в течение 5 лет в конце года платежи. Первый платеж равен 3 тыс. грн., а каждый следующий год по отношению к предыдущему увеличивается на 15%

Необходимо оценить такой аннуитет, если банк начисляет в конце каждого года сложные проценты из расчета 12% годовых.

Увеличение платежа на 15% означает его рост в1,15 раза, т.е. поток платежей образует геометрическую прогрессию с знаменателем q =1,15.

тыс. грн.

тыс. грн.

Используя вышеприведенные формулы для расчета будущей и приведенной стоимости аннуитета можно напистаь в явном виде формулы для определения только величины аннуитета:

Что касается знаменателя геометрической прогрессии, процентной ставки и продолжительности аннуитета, то эти параметры могут быть определены только с помощью приближенных методов.

Если же члены переменного аннуитета не образуют ни арифметическую, ни геометрическую прогрессию, то, тем не менее, во многих случаях оценка таких аннуитетов может быть выполнена с помощью финансовых таблиц. Рассмотрим технику подобных вычислений на следующем примере.

Пример.

Садовый участок сдается в аренду на 10 лет. Арендная плата будет осуществляться ежегодно по схеме постнумерандо на следующих условиях: в первые шесть лет – по 10 тыс. грн., а в оставшиеся четыре года – по 11 тыс. грн.

Требуется оценить приведенную стоимость этого договора, если процентная ставка, используемая аналитиком, равна 15%.

Решать данную задачу можно различными способами, в зависимости от того, какие аннуитеты будут выделены аналитиком.

Ествественн, приведенная стоимость денежного потока должна оцениваться с позиции начала первого временного интервала.

Рассмотрим два возможных варианта. Оба варианта основываются на свойстве аддитивности рассмотренных алгоритмов в отношении величины аннуитетного платежа.

1) Исходный поток можно представить как сумму двух аннуитетов: первый имеет А = 10 тыс. грн. и продолжается 10 лет, второй имеет А = 1 тыс. грн. и продолжается четыре года.

По формуле оцениваем приведенную стоимость каждого аннуитета. Однако второй аннуитет в этом случае будет оценен с позиции начала седьмого года. Поэтоому полученную сумму необходимо дисконтировать с помощью формулы к началу первого года. В этом случае оценки двух аннуитетов будут приведены к одному моменту времени, а их сумма даст оценку приведенной стоимости исходного денежного потока:

тыс. грн.

2) Исходный поток можно представить как разность двух аннуитетов: первый имеет А = 11 тыс. грн. и продолжается десять лет; второй имеет А = 1 тыс. грн. и, начавшись в первом году, заканчивается в шестом. В этом случае расчет выглядит так:

тыс. грн.

Аннуитеты с периодом, большим, чем базовый.

Ранее были рассмотрены аннуитеты, периоды которых не превосходили базовые периоды начисления процентов. В частности, мы говлрили, что если базовый период равен году, то период аннуитета не превышал одного года. Однако, в финансовых операциях бывают случаи срочных аннуитетов, у которых их период больше года. Предположим, речь идет о срочном аннуитете с денеежными поступлениями каждые два года.

Предположим есть постоянный аннуитет постнумерандо, денежные поступления которого каждое в размере А происходят в течение n периодов, являющихся базовым для начисления процентов по ставке r. Причем денежные поступления происходят каждые u периодов, а начисление сложных процентов – в конце каждого периода. Оценим будущую стоимость аннуитета.

Последнее поступление равняется А. На предпоследнее поступление начисляются сложные проценты за u периодов и оно будет равно . На поступление начисляютя сложные проценты за 2u периодов и оно будет равно и т.д. до первого включительно, которое равняется

Полученные величины образуют геометрическую прогрессию с первым членом А, знаменателем и числом членов, равным u. Поэтому сумма этих величин будет равна:

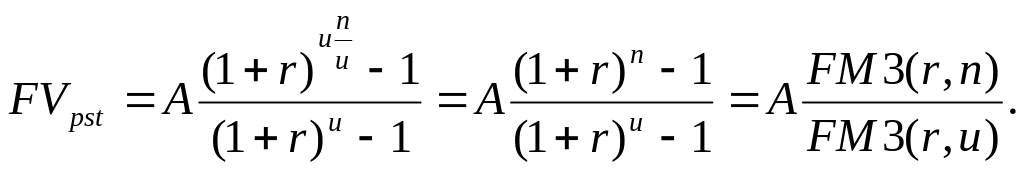
Пример.

Работник заключает с фирмой пенсионный контракт на 10 лет, согласно которому на счет работника в банке в конце каждого двухлетнего периода будет поступать 1,4 тыс. грн.

Требуется определить наращенную к концу действия контракта сумму, если на денежные поступления будут ежегодно начисляться декурсивные сложные проценты по ставке 12% годовых.

В соответствии с контрактом денежные суммы образуют аннуитет длительностью 10 лет и периодом 2 года. Т.о. период аннуитета больше базового периода начисления процентов.

тыс. грн.

Если начисление сложных процентов происходит раз m в течение этого периода, то для нахождения будущей стоимости аннуитета используется следующая формула:

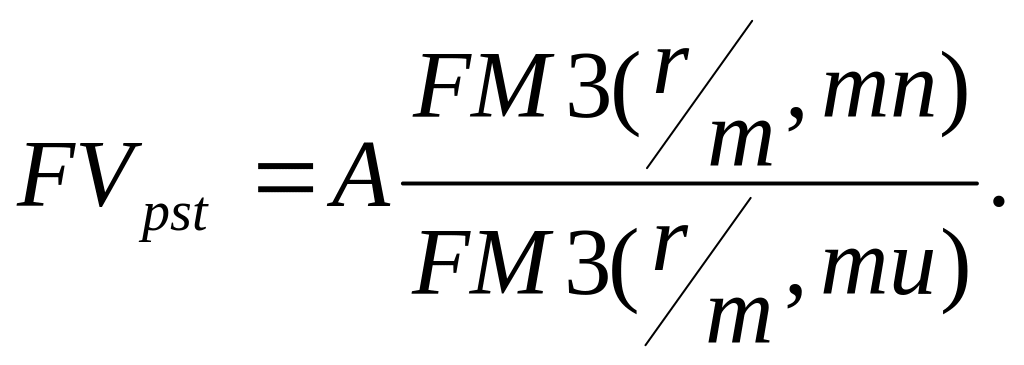
Пример.

Фирма решила образовать фонд для обеспечения будущих расходов, связанных с реконструкцией производства. С этой целью в конце каждых трех лет фирма перечисляет в банк 8 тыс. грн.

Какая сумма будет на счете фирмы через 15 лет, если на поступающие суммы будут ежеквартально начисляться сложные проценты по номинальной годовой процентной ставке 16%?

тыс. грн.

Если начисление сложных процентов происходит раз за базовый период и необходимо найти приведенную стоимость будущих поступлений то используется формула:

Откуда:

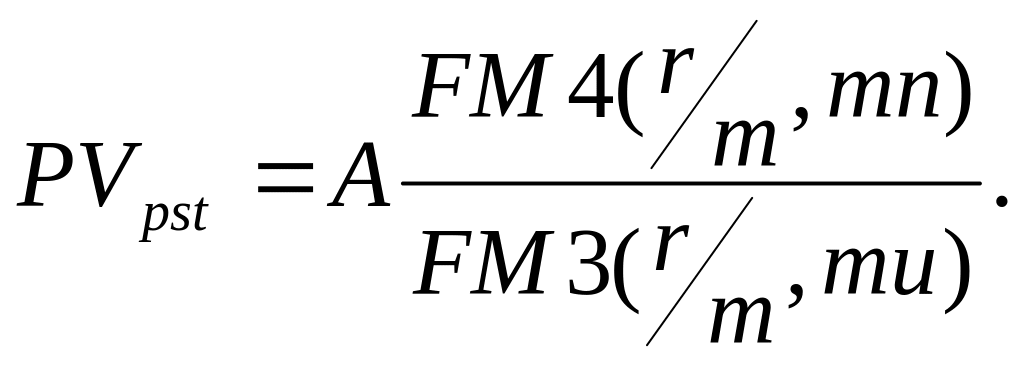
Пример.

Определить сумму, которую необходимо поместить на счет в банке, чтобы в течение 8 лет в конце каждого двухлетнего периода иметь возможность снимать со счета 3 тыс. грн., причем к концу срока полностью выбрать все деньги со счета, если на находящиеся на счете денежные суммы будут начисляться каждые полгода сложные проценты по ставке 12% годовых.

тыс. грн.

Формулы для оценок аннуитета пренумерандо получаются из соответствующих формул для оценки аннуитета постнумерандо:

и