§1.3. Необходимое условие сходимости ряда. Гармонический ряд
Теорема о необходимом условии сходимости ряда.
Если ряд
сходится, то предел последовательности
общих членов этого ряда равен нулю:
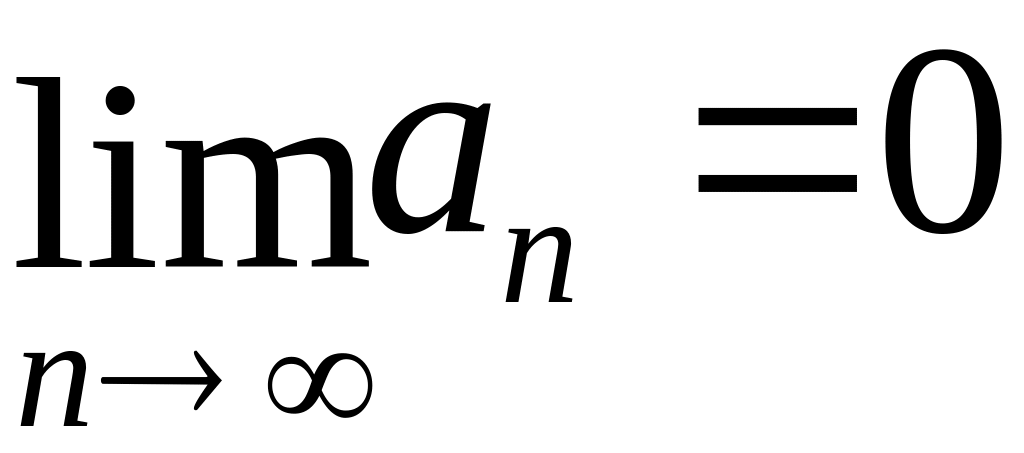. (1.11)
Другая формулировка. Для того чтобы ряд сходился, необходимо (но недостаточно!), чтобы предел последовательности общих членов ряда был равен нулю.
Замечание. Иногда для краткости слово «последовательность» опускают и говорят: «предел общего члена ряда равен нулю». То же для последовательности частичных сумм («предел частичной суммы»).
Доказательство теоремы. Представим общий член ряда в виде (1.10):
.
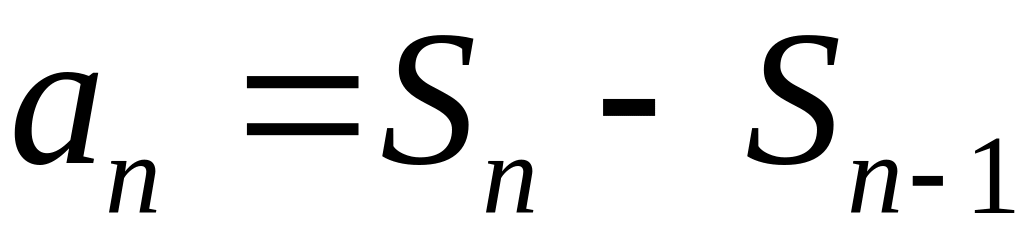По
условию ряд сходится, следовательно,
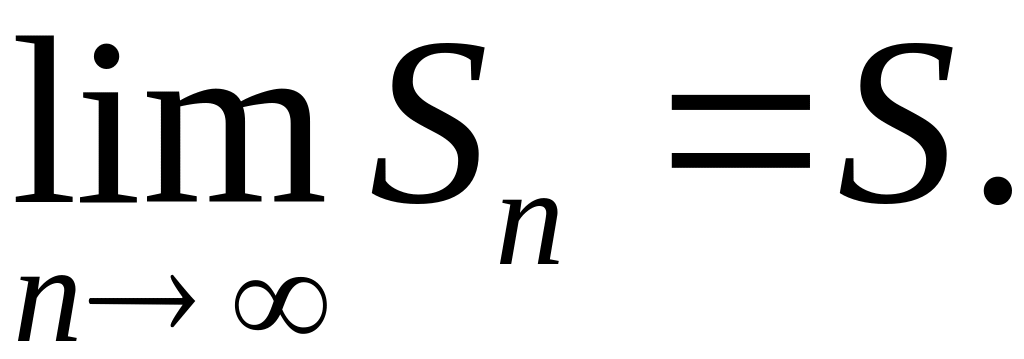Очевидно, что и
,
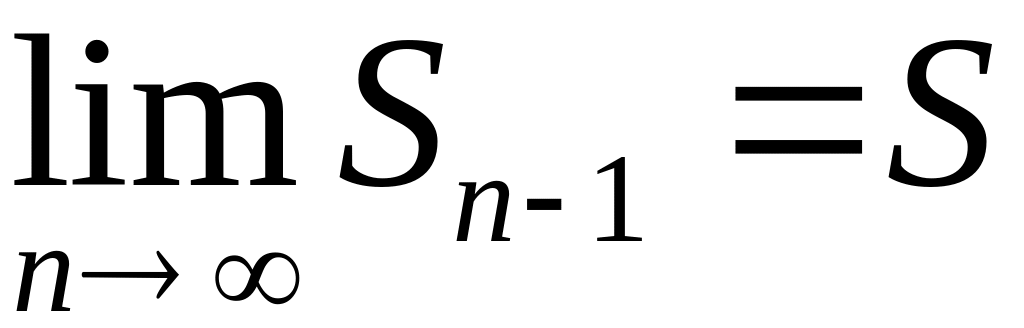т.к. п
и п-1
стремятся к бесконечности одновременно
.
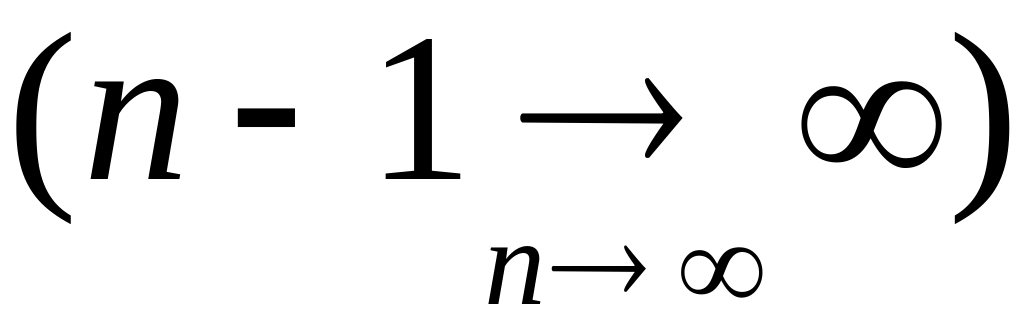Найдем предел последовательности общих
членов ряда:
,
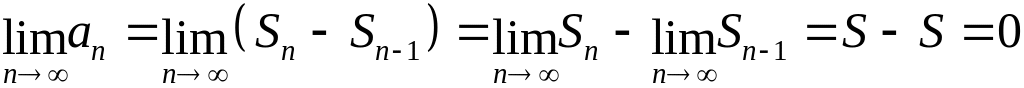ч.т.д.
Замечание. Обратное утверждение неверно. Ряд, удовлетворяющий условию (1.11), не обязательно сходится. Поэтому условие, или признак (1.11) является необходимым, но не является достаточным признаком сходимости ряда.
Пример 1. Гармонический ряд. Рассмотрим ряд
(1.12)
Этот ряд называется гармоническим, т.к. каждый его член, начиная со второго, является средним гармоническим соседних с ним членов:
.
Например:
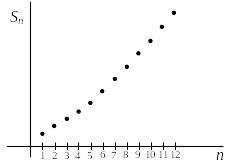
Рис.1.3.1 Рис.1.3.2
Общий член
гармонического ряда удовлетворяет
необходимому условию сходимости ряда
(1.11):
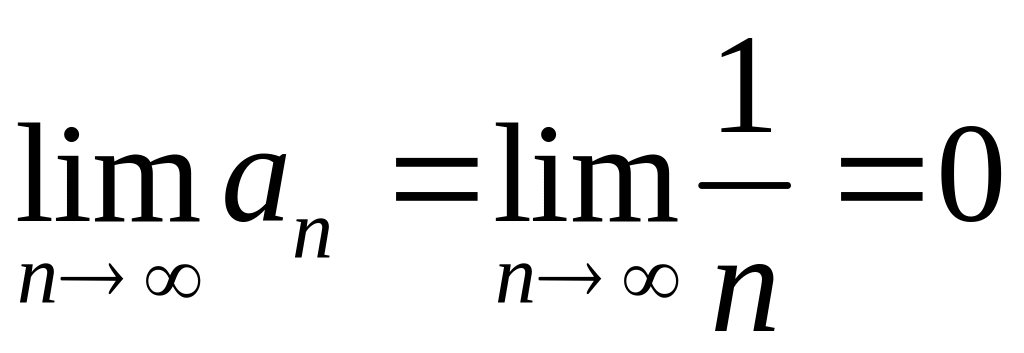(рис.1.3.1). Однако в дальнейшем будет
показано (с помощью интегрального
признака Коши), что этот ряд расходится,
т.е. его сумма равна бесконечности. На
рис.1.3.2 показано, что частичные суммы
неограниченно возрастают при увеличении
номера.
Следствие.
Из необходимого условия сходимости
ряда вытекает достаточный
признак расходимости ряда:
если
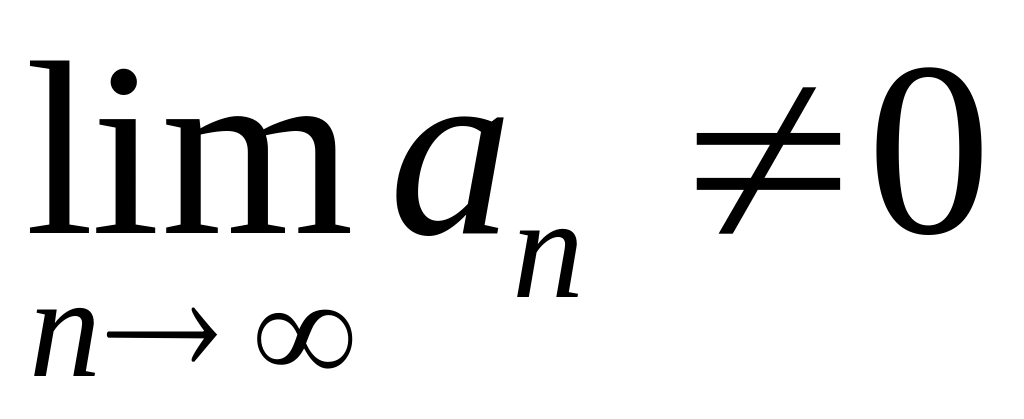или не существует, то ряд расходится.
Доказательство.
Предположим противное, т.е.
(или не существует), но ряд сходится. Но
согласно теореме о необходимом условии
сходимости ряда предел общего члена
должен быть равен нулю:
.
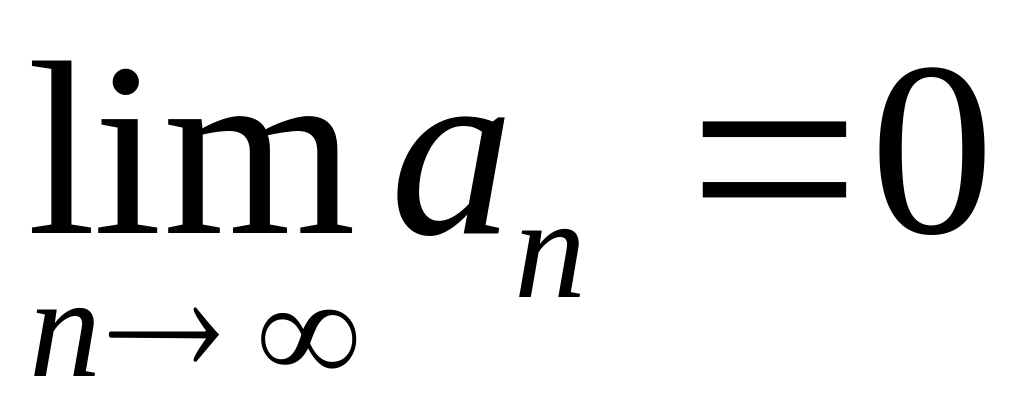Противоречие.
Пример
2.
Исследовать на сходимость ряд с общим
членом
.
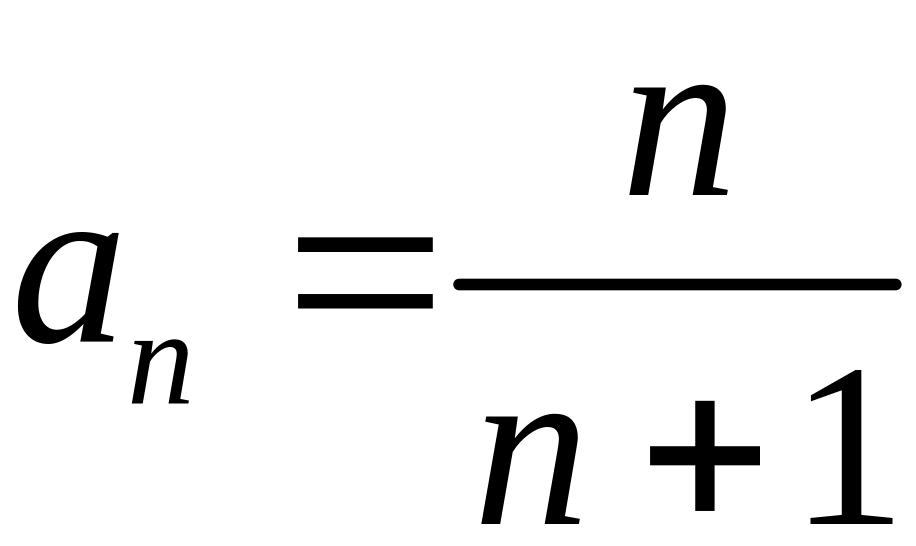Данный ряд имеет
вид:
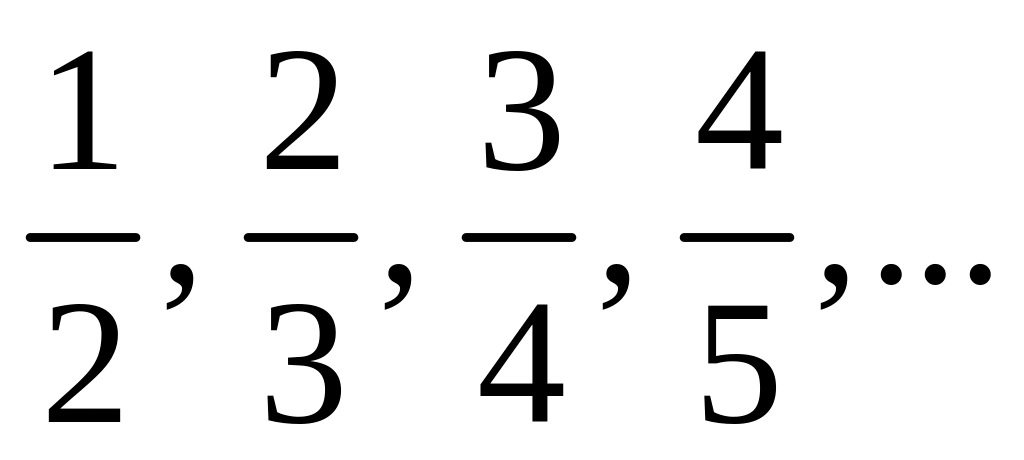
Найдем предел общего члена ряда:
.
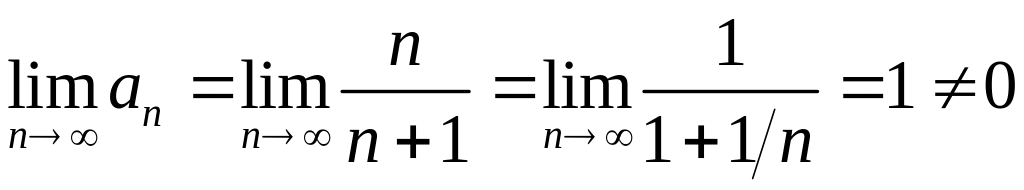Согласно следствию данный ряд расходится.
§1.4. Ряд, образованный геометрической прогрессией
Рассмотрим ряд, составленный из членов геометрической прогрессии. Напомним, что геометрической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число, не равное нулю и называемое знаменателем этой прогрессии. Геометрическая прогрессия имеет вид:
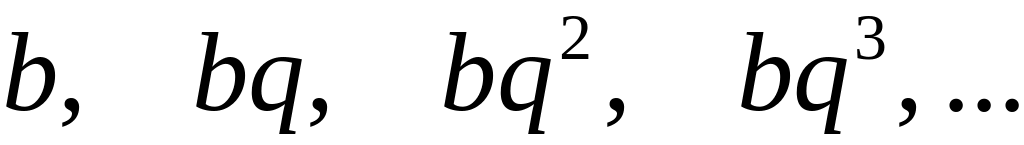
а ряд, составленный из ее членов:
Такой ряд называется геометрическим рядом, но иногда для краткости его называют просто геометрической прогрессией. Название «геометрическая» прогрессия получила потому, что каждый ее член, начиная со второго, равен среднему геометрическому соседних с ним членов:
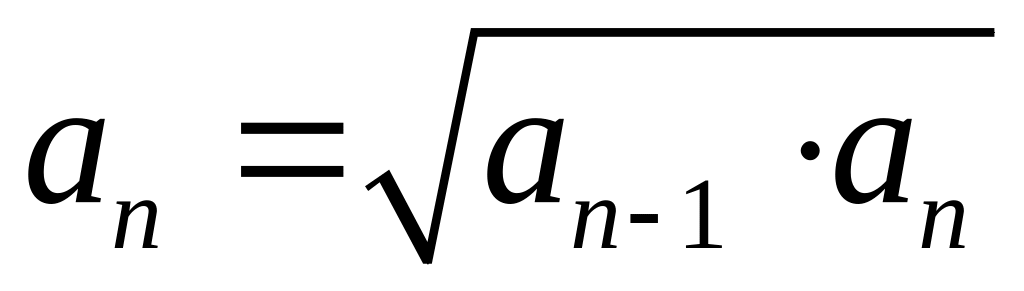, или
.
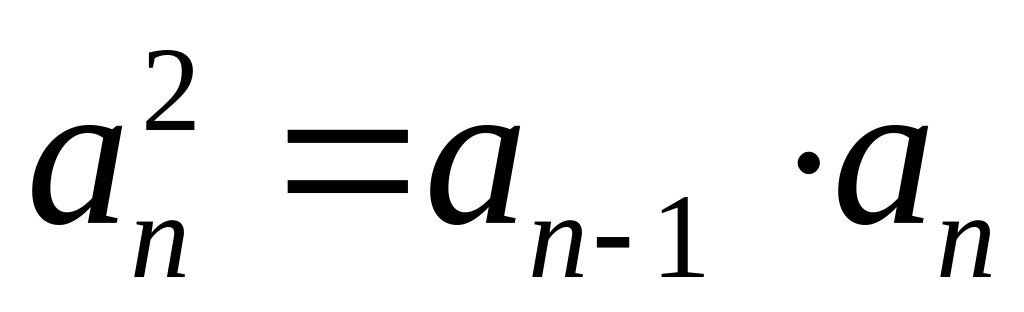Теорема. Ряд, составленный из членов геометрической прогрессии
(1.13)
расходится
при
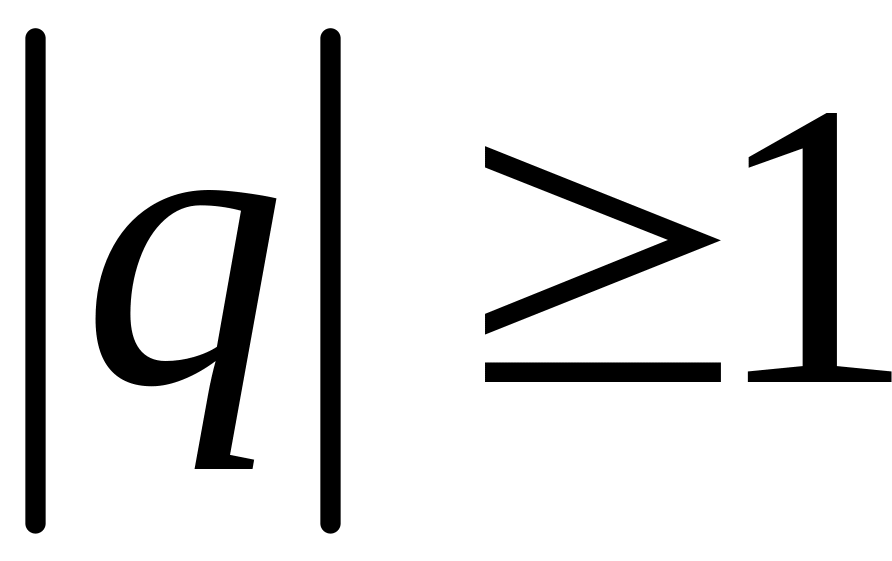и сходится при
,
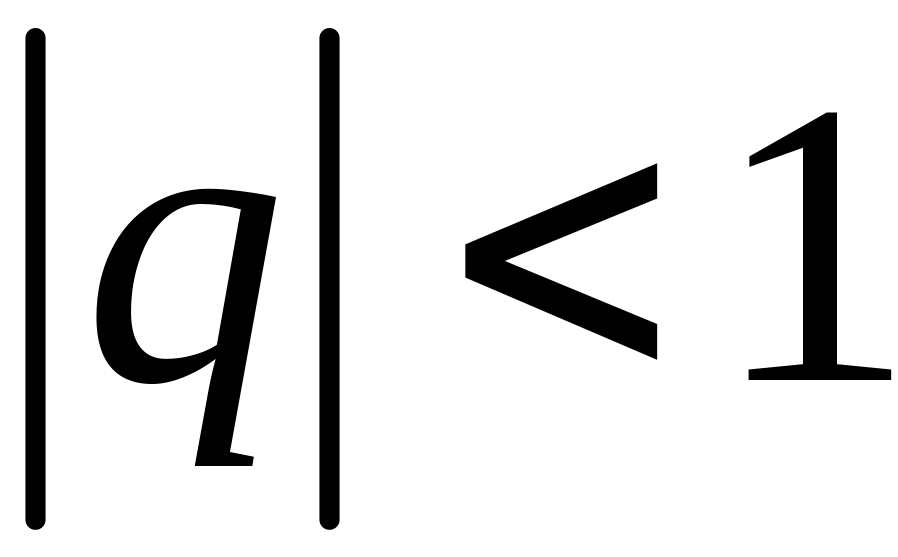причём при
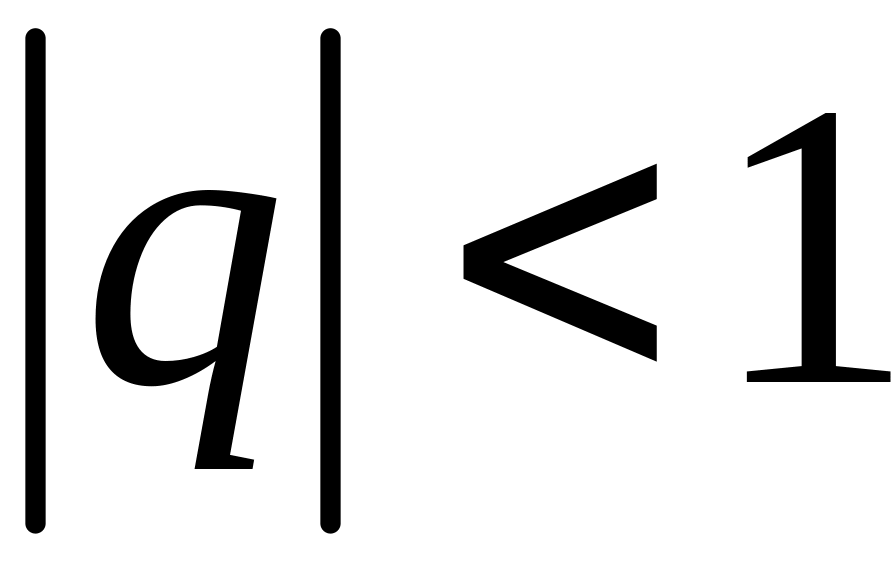сумма ряда
(1.14)
Доказательство.
Общий член ряда, как и общий член
геометрической прогрессии, имеет вид:
.
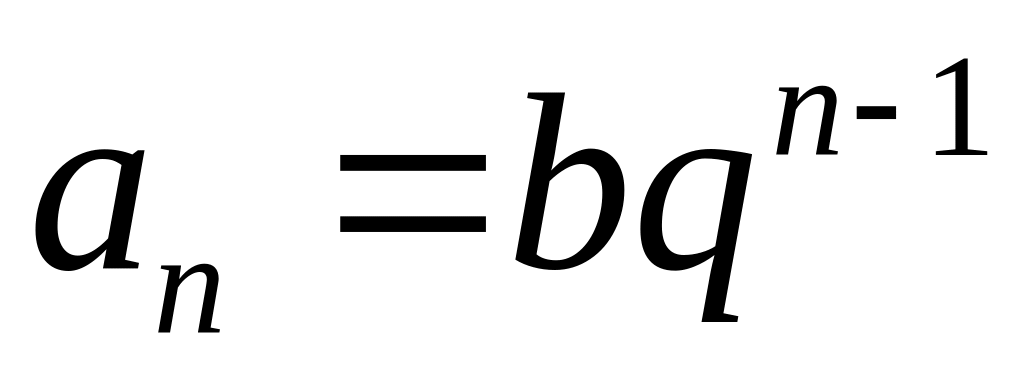1) Если
,
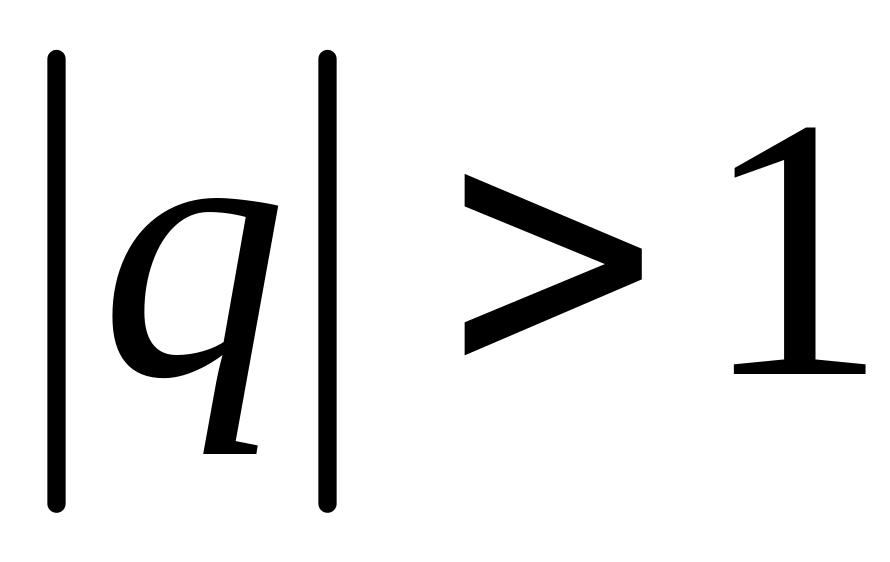то
,
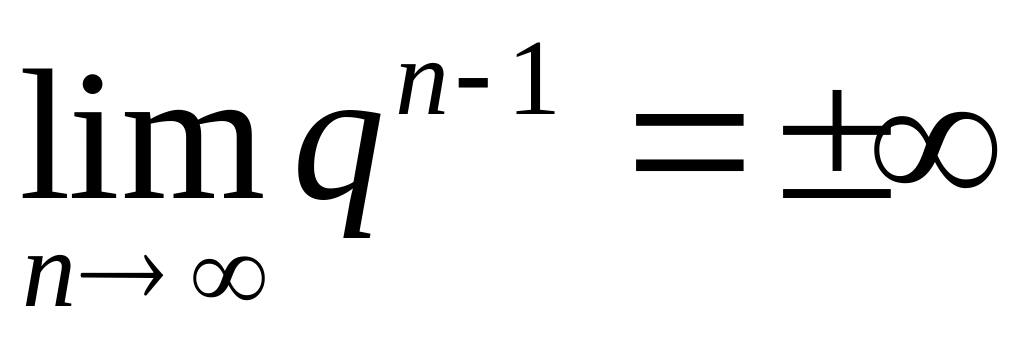т.к. в этом случае
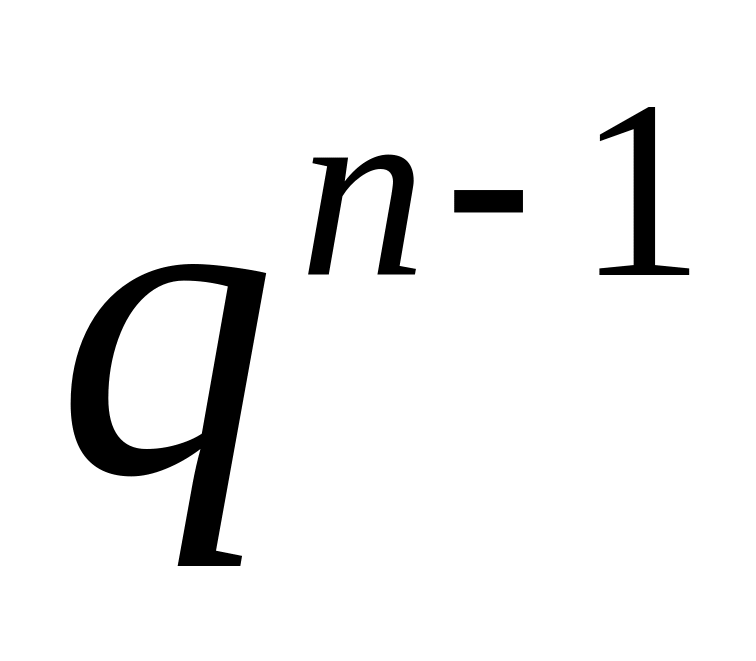– бесконечно большая величина.
2) При
ряд ведёт себя по-разному, т.к. приобретает
различные виды.
При
;
,
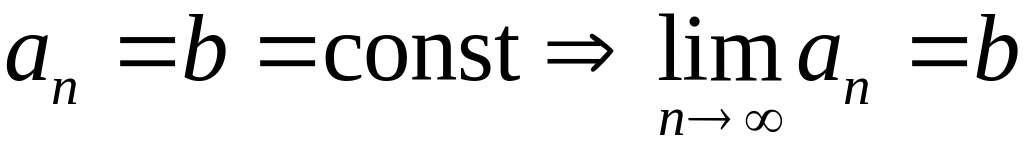т.к. предел константы равен самой
константе. Т.к. по условию теоремы
,
общий член ряда не стремится к нулю.
При
;
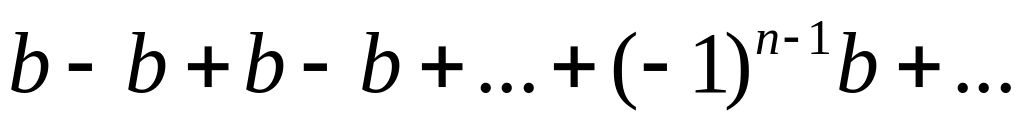предела не существует.
Таким
образом, при
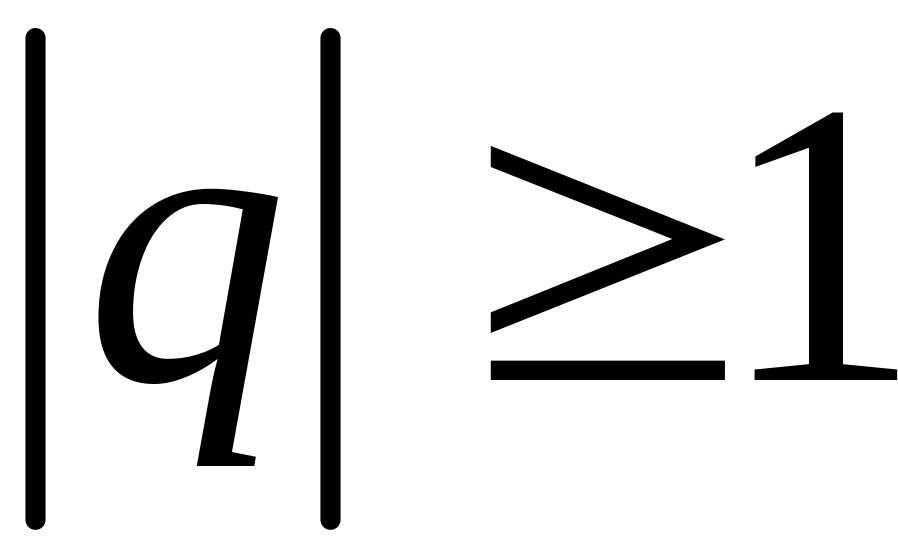не выполняется необходимое условие
сходимости ряда:
.
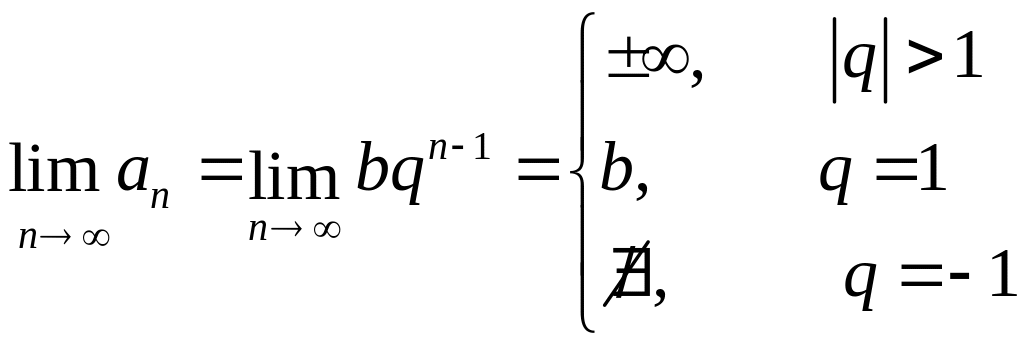Следовательно, ряд (1.13) расходится.
3) Если
,
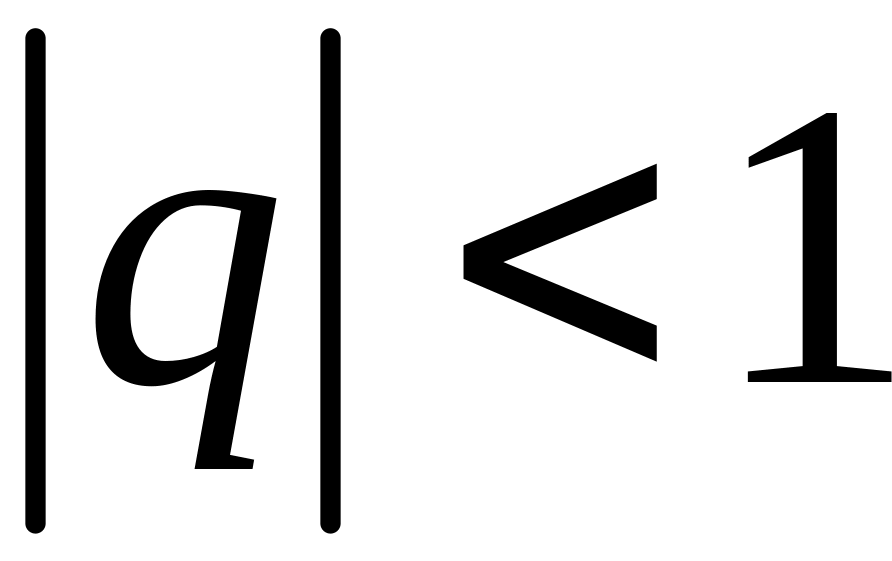то прогрессия называется бесконечно
убывающей. Из школьного курса известно,
что n-ю
частичную сумму ряда (1.13) можно представить
в виде:
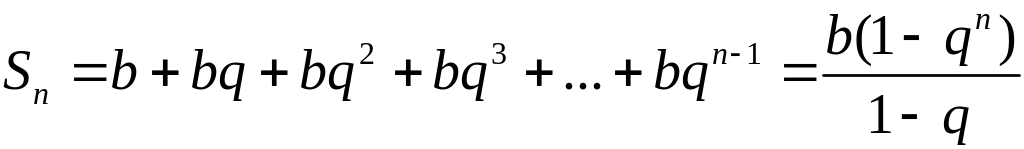. (1.15)
Найдём
сумму ряда. Так как при
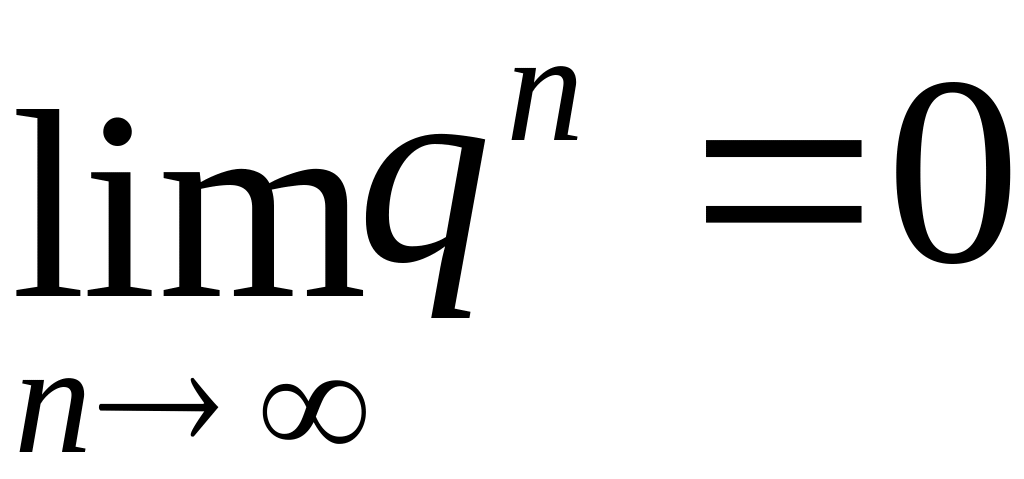(бесконечно малая величина), то
.
Таким
образом, при
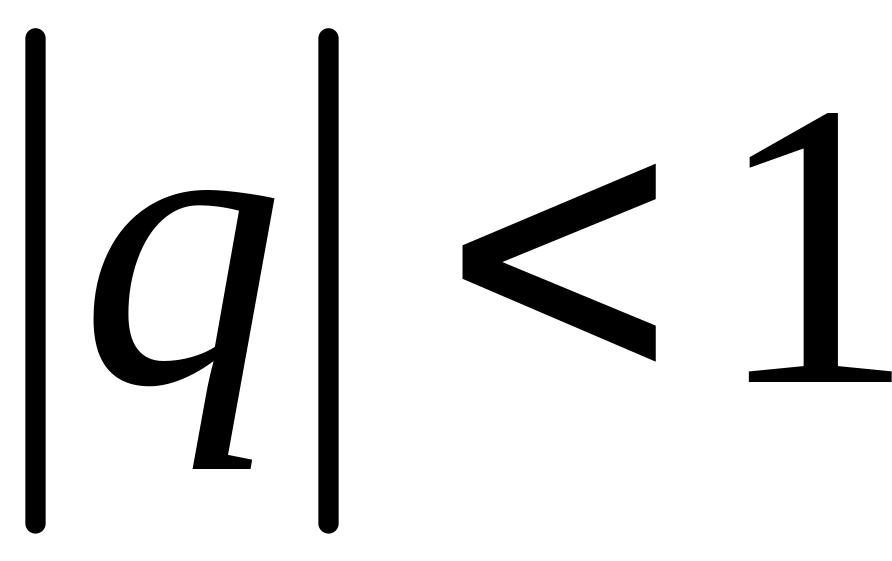ряд (1.13) сходится и имеет сумму, равную
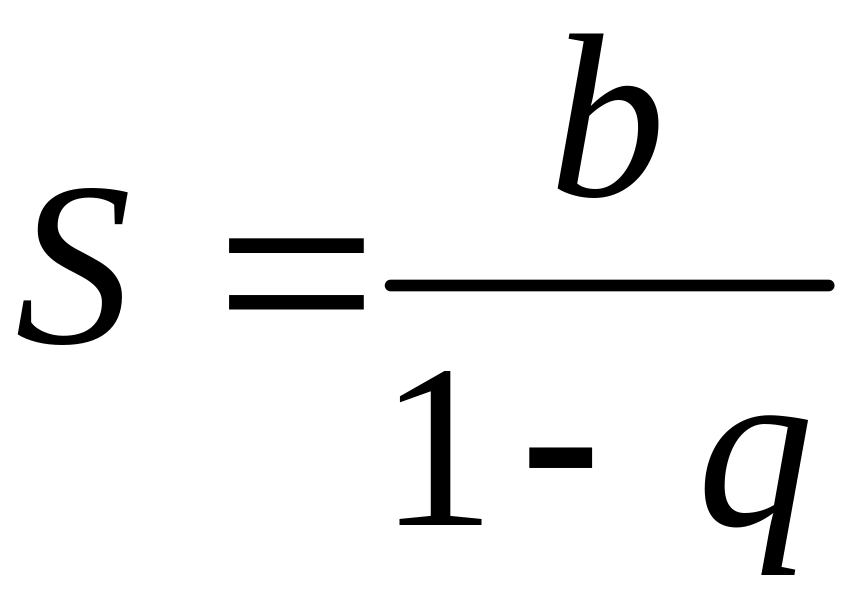. (1.16)
Это и есть сумма бесконечно убывающей геометрической прогрессии.
Пример 1º.
Рис.1.4.1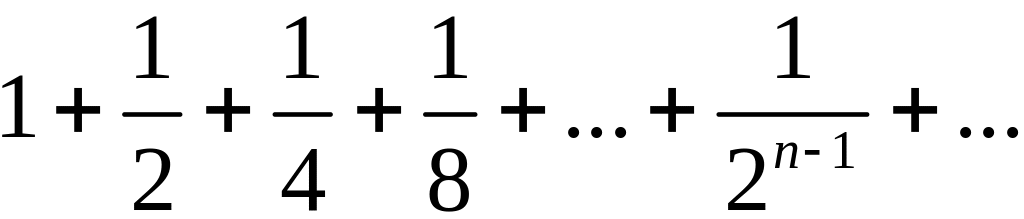
=2.
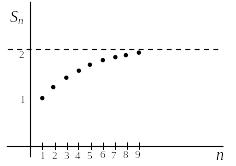
Оценим его сумму, т.е. попробуем определить, к чему стремится последовательность его частичных сумм.
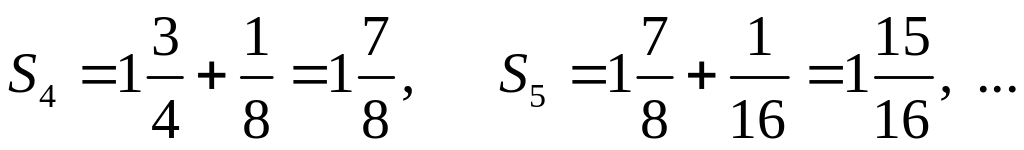
Видно, что последовательность частичных сумм стремится к числу 2 (рис.1.4.1).
А теперь докажем
это. Воспользуемся тем, что данный ряд
это ряд, составленный из членов
геометрической прогрессии, где
.
Сумма бесконечно убывающей геометрической
прогрессии
.
Пример 2º.
.
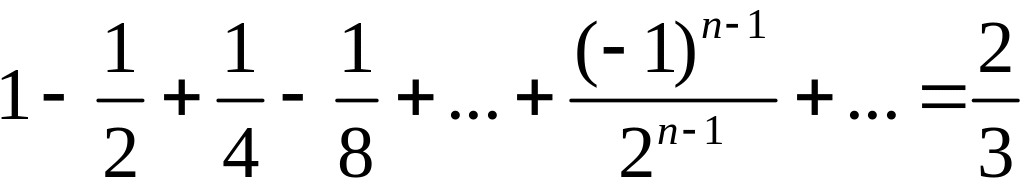Вычисляется аналогично. Поскольку многие из членов ряда в отличие от предыдущего примера имеют знак минус, то сумма оказалась меньше.
Пример 3º.
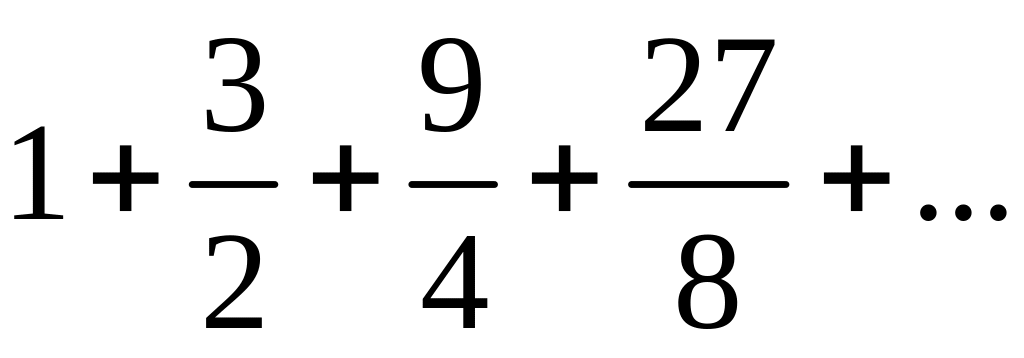
Это геометрический
ряд, где
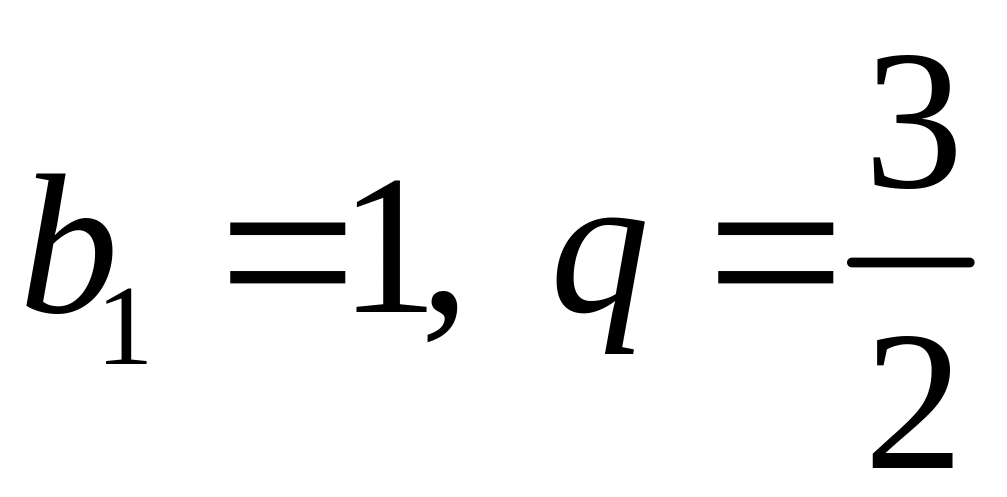>1.
Такой ряд расходится.