§1.6. Знакоположительные ряды
Рассмотрим ряд с неотрицательными членами
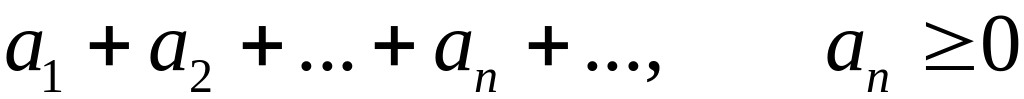, (1.26)
Т
акие
ряды будем называть знакоположительными.
Рассмотрим последовательность частичных
сумм
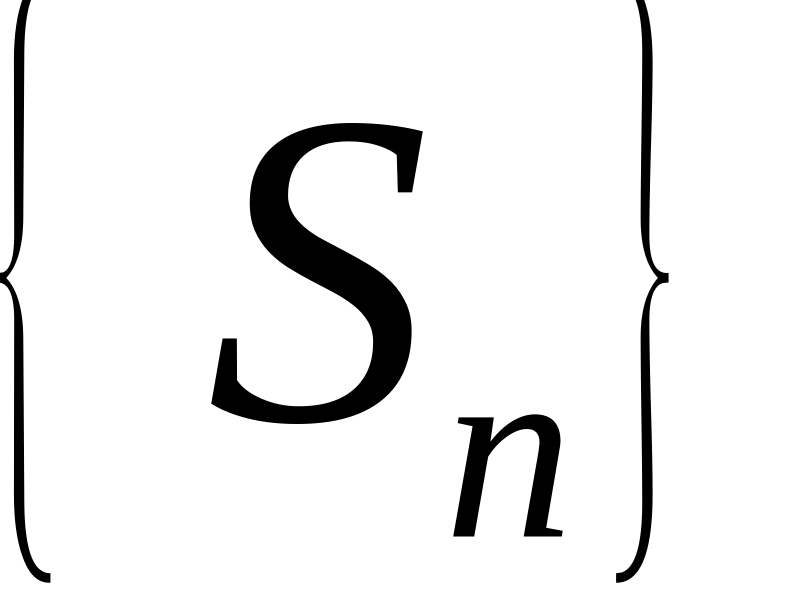знакоположительного ряда (1.26). Поведение
этой последовательности особенно
простое: она монотонно возрастает при
возрастании n,
т.е.
.
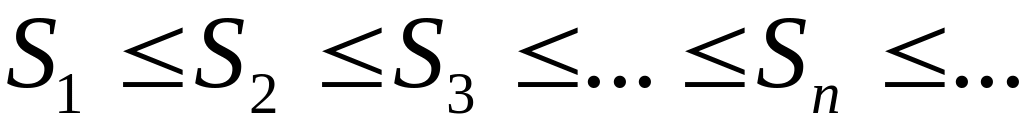(т.к. к каждой последующей частичной
сумме прибавляется неотрицательное
число).
Согласно теореме Вейерштрасса любая монотонная ограниченная последовательность сходится (см. I семестр I курса). Исходя из этого, сформулируем общий критерий сходимости рядов с положительными членами.
Теорема (общий критерий сходимости знакоположительных рядов). Для того, чтобы знакоположительный ряд сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.
Напомним определение
ограниченности последовательности:
последовательность называется
ограниченной, если существует М>0
такое, что для
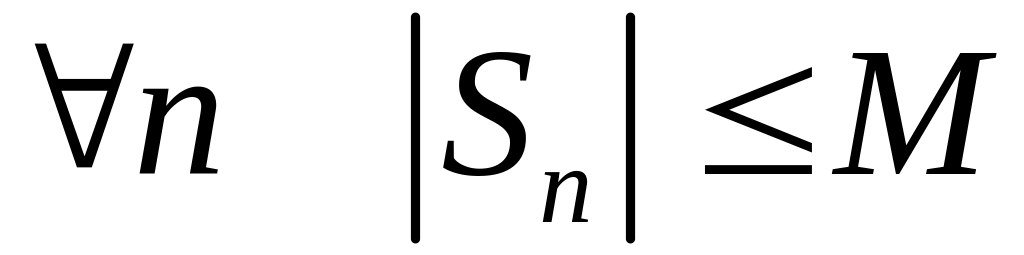(рис.1.6.1). Для знакоположительных рядов
,
и можно говорить об ограниченности
сверху, т.к. снизу
ограничена нулём.
Доказательство. 1) Необходимость. Пусть ряд (1.26) сходится последовательность частичных сумм имеет предел, т.е. сходится. По теореме об ограниченности сходящейся последовательности любая сходящаяся последовательность ограничена ограничена.
2) Достаточность. Пусть последовательность частичных сумм ряда (1.26) ограничена.
Т.к.
,
т.е.
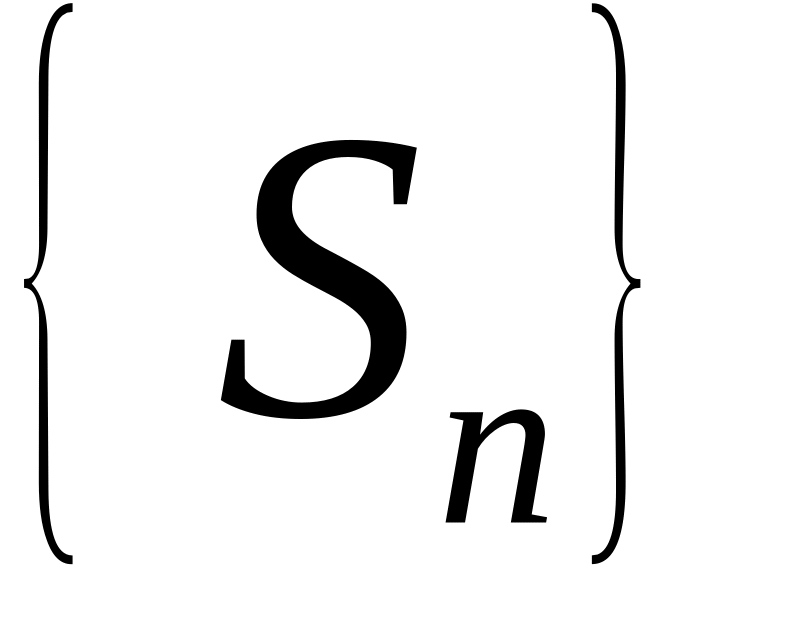монотонна. По теореме Вейерштрасса о
монотонных ограниченных последовательностях
она сходится
сходится ряд (1.26).
Ясно, что при неограниченном возрастании последовательности частичных сумм ряд расходится.
Общий критерий сходимости знакоположительных рядов позволяет установить достаточные признаки сходимости рядов с положительными членами. Этими признаками являются:
1) признаки сравнения рядов;
2) признак Даламбера;
3) признаки Коши.
§1.7. Первый признак сравнения
Теорема о первом признаке сравнения.
Пусть даны два ряда с неотрицательными членами:
(1.27)
(1.28)
причем, начиная с некоторого номера nN, выполняется неравенство
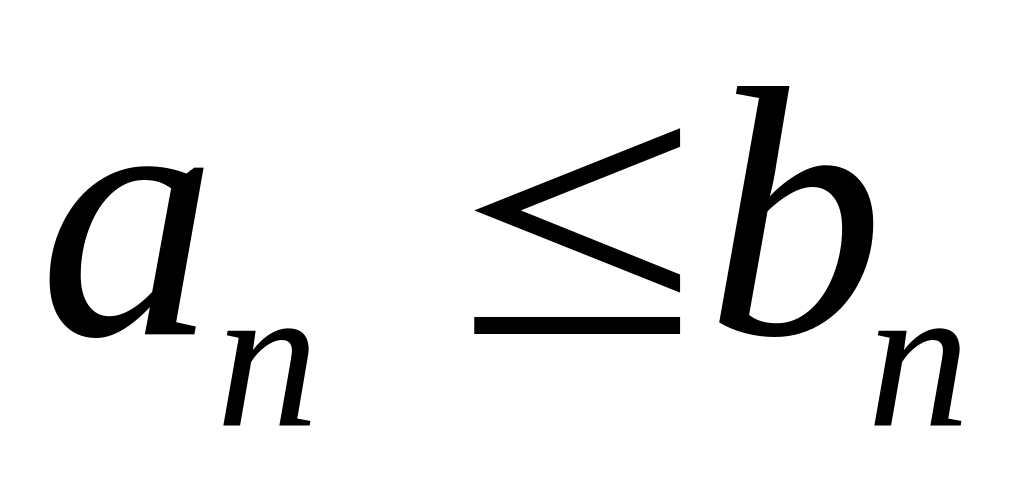. (1.29)
Тогда:
1) из сходимости ряда (1.28) следует сходимость ряда (1.27);
2) из расходимости ряда (1.27) следует расходимость ряда (1.28).
Д
ругими
словами, если сходится больший ряд, то
сходится и меньший, если расходится
меньший ряд, то больший расходится и
подавно (рис.1.7.1).
Доказательство.
1) Пусть
и
частичные суммы рядов (1.27) и (1.28),
соответственно. Т.к.
,
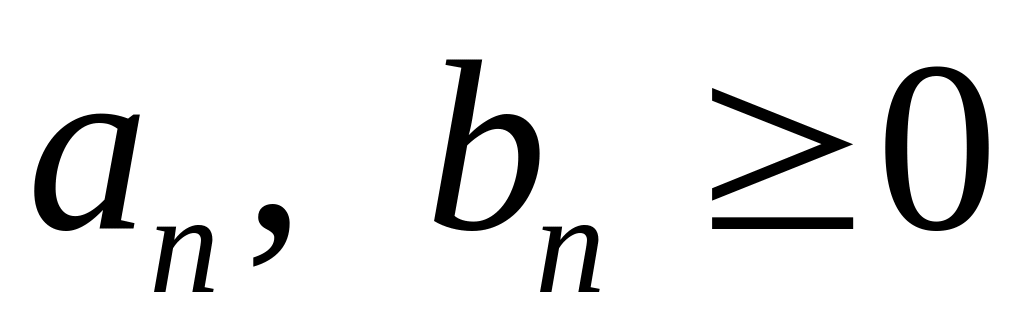из соотношения (1.29) следует, что
(сумма меньших чисел меньше суммы больших
чисел). Если ряд
сходится, то последовательность его
частичных сумм
ограничена (сверху), но тогда ограничена
и последовательность частичных сумм
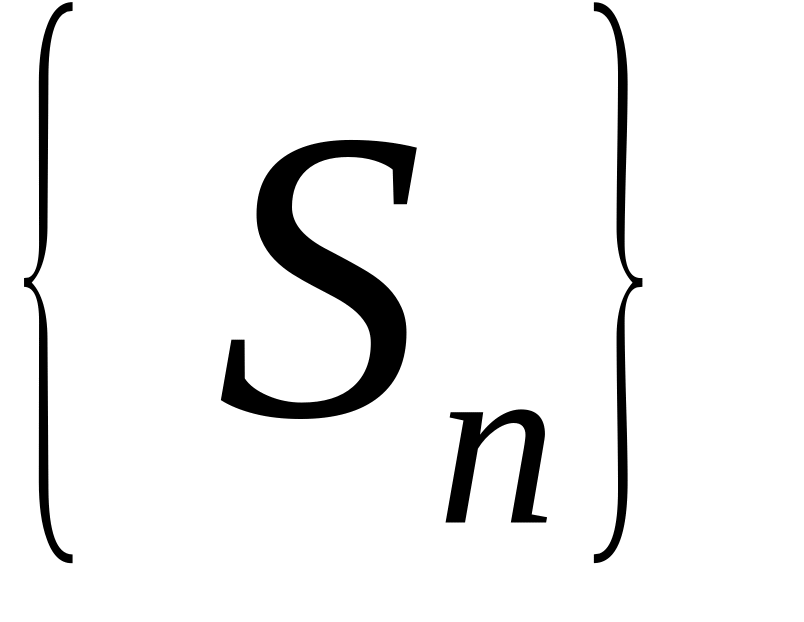ряда
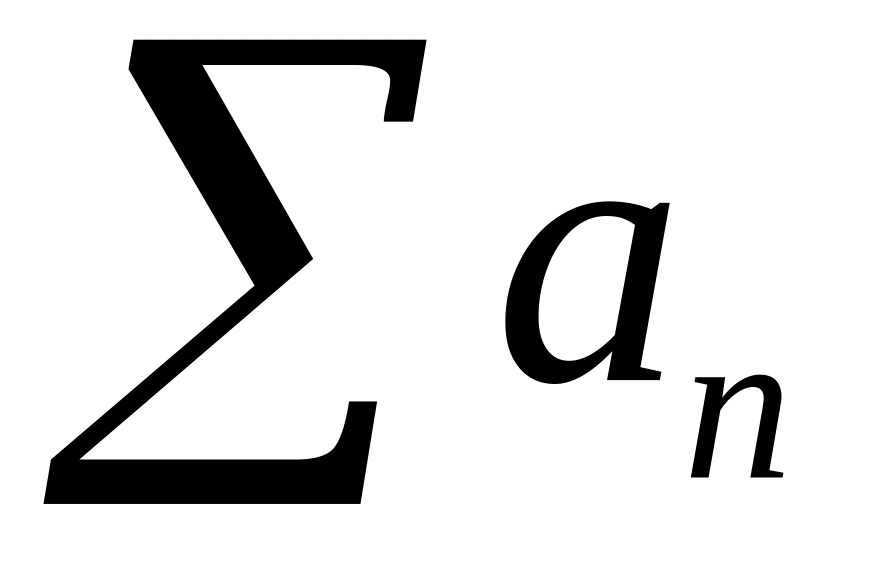как ряда с меньшими членами;
согласно общему критерию сходимости
ряд
сходится.
2) Пусть теперь ряд расходится. Предположим, что при этом ряд сходится. Но тогда по только что доказанному меньший ряд также должен сходиться. Противоречие. Следовательно, ряд расходится.
Признак
сравнения применяется для исследования
сходимости знакоположительных рядов,
если известна сходимость какого-либо
другого ряда, годного для сравнения с
заданным рядом. Чаще всего сравнивают
с геометрической прогрессией (сходится
при
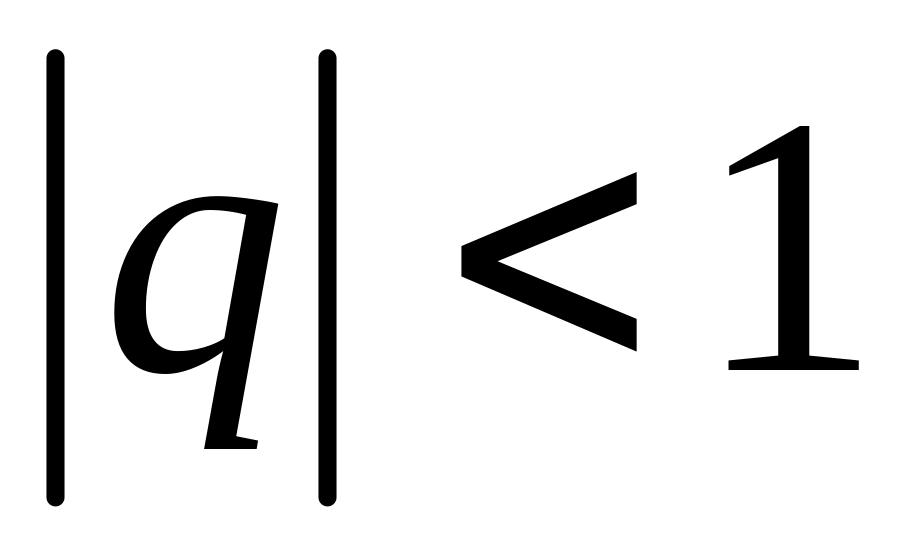и расходится при
)
и с обобщённым гармоническим рядом
,
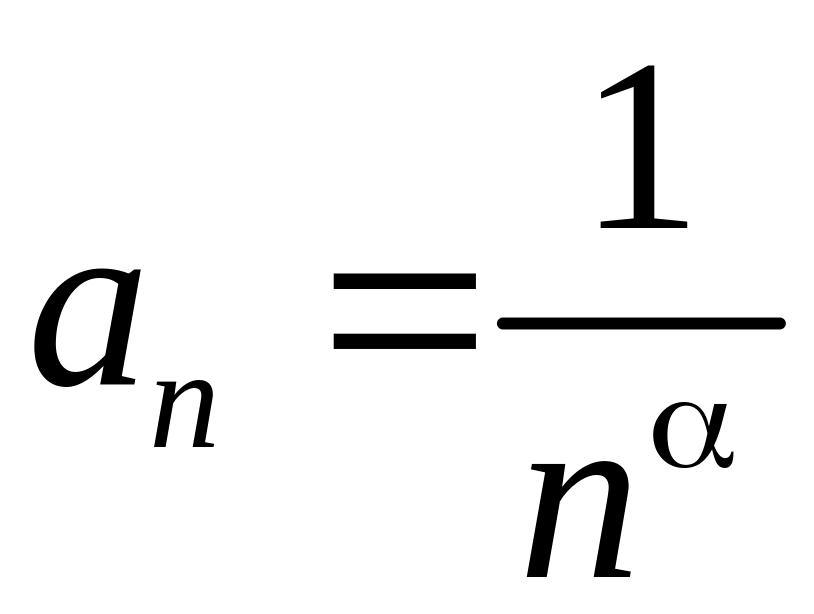который сходится при >1
и расходится при 1
(доказательство будет приведено позже).
Пример
1. 
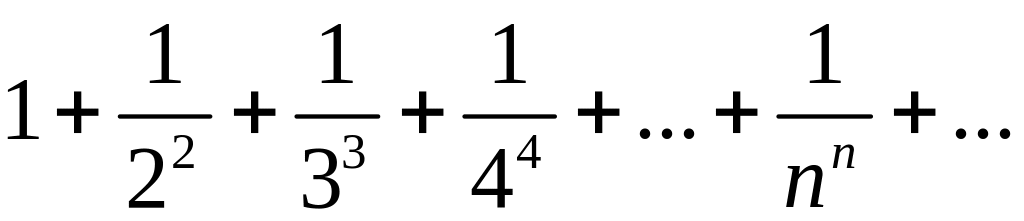
Сравним данный ряд с бесконечной геометрической прогрессией:
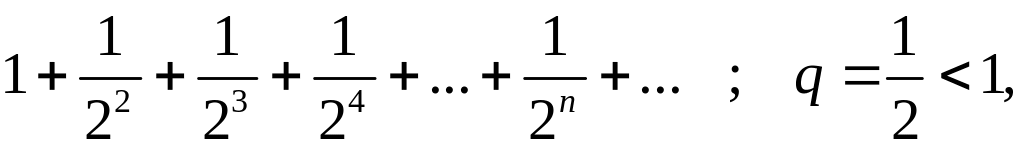которая сходится.
Так
как начиная с n=3
,
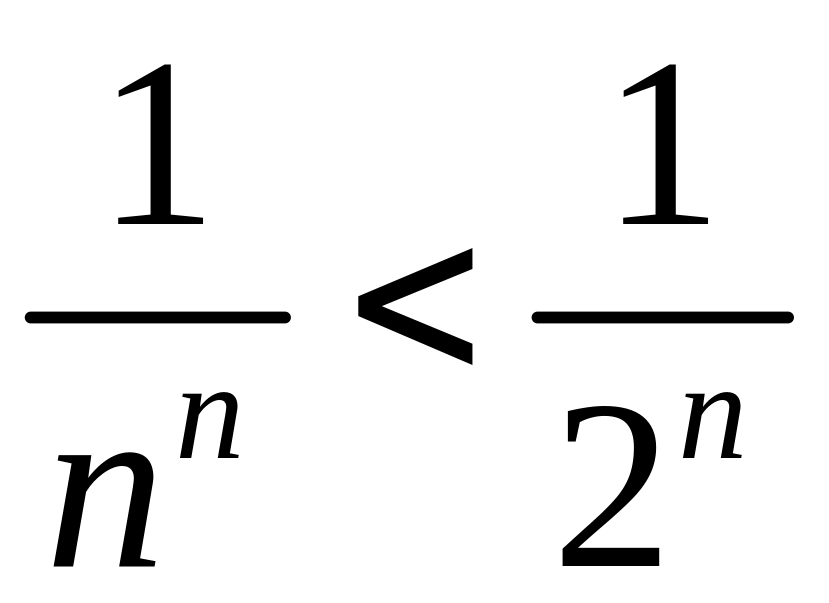то данный ряд сходится.
Пример
2.
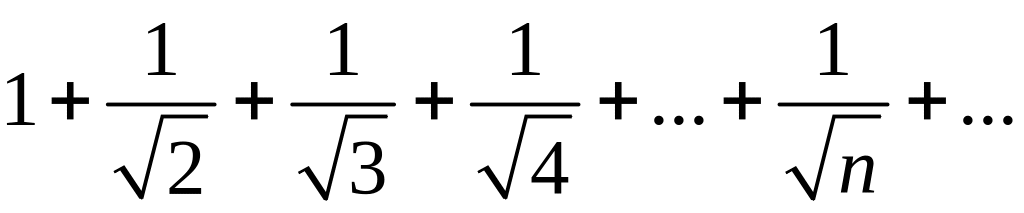
Сравним
данный ряд с расходящимся гармоническим
рядом
.
Так
как начиная с п=2
,
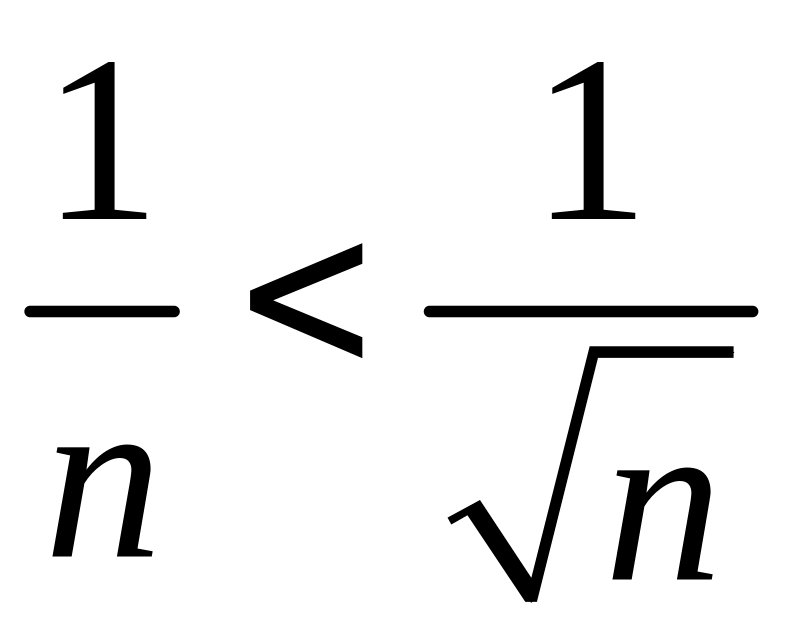то данный ряд расходится.
Замечание.
Данный ряд является обобщенным
гармоническим рядом,
.