§1.5. Свойства сходящихся рядов

Рассмотрим два сходящихся ряда:

, (1.17)

. (1.18)

1. Ряд, полученный почленным сложением (вычитанием) двух сходящихся рядов, также сходится, а его сумма равна алгебраической сумме исходных рядов, т.е.

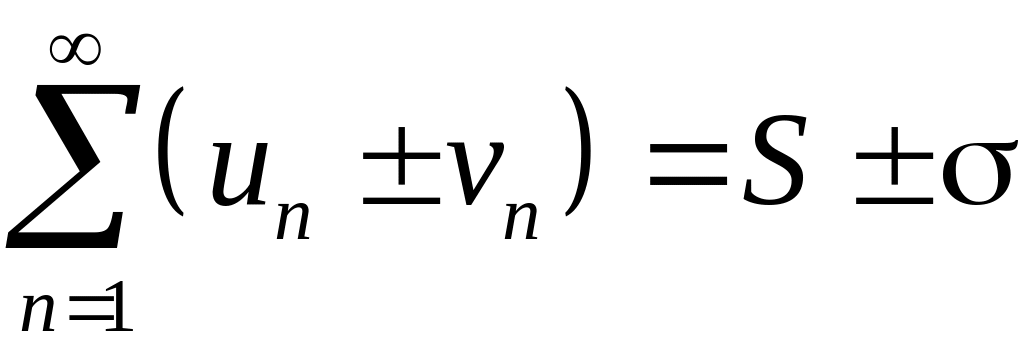. (1.19)

Доказательство. Составим частичные суммы рядов (1.17) и (1.18):

.

Т.к. по условию данные ряды сходятся, существуют пределы этих частичных сумм:

, .

Составим частичную сумму ряда (1.19) и найдём её предел:

;

, ч.т.д.

Пример.

;

.

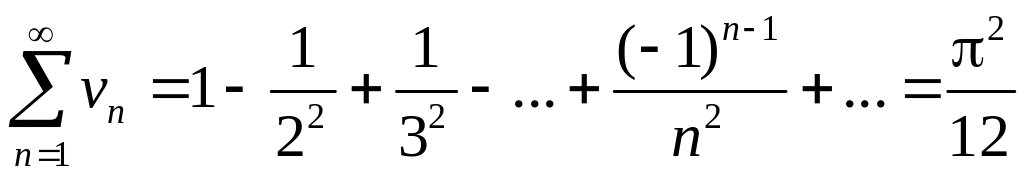Замечание. Обратное утверждение неверно, т.е. из сходимости ряда, стоящего в левой части равенства (1.19), не следует сходимость рядов и . Например, ряд, рассмотренный в примере 4, сходится, и его сумма равна 1; общий член этого ряда был преобразован к виду:

.

Следовательно, ряд можно записать в виде:

.

Рассмотрим теперь отдельно ряды:

Эти ряды расходятся, так как являются гармоническими рядами. Таким образом, из сходимости алгебраической суммы рядов не следует сходимость слагаемых.

2. Если все члены сходящегося ряда с суммой S умножить на одно и то же число с, то полученный ряд также будет сходиться и иметь сумму cS:

. (1.20)

Доказательство аналогично первому свойству (доказать самостоятельно).

Пример. 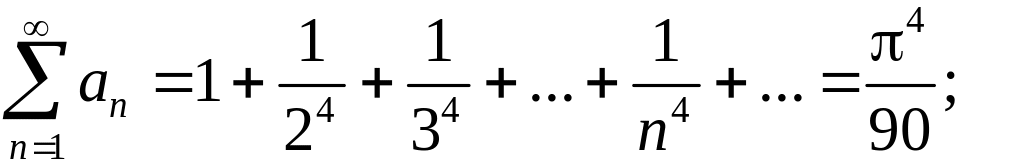с=10000;

.

Оба ряда сходятся, т.к. их суммы конечны.

Таким образом, сходящиеся ряды можно почленно складывать, вычитать и умножать на постоянный множитель.

3. Теорема об отбрасывании нескольких первых членов ряда.

Отбрасывание (или добавление) нескольких первых членов ряда не влияет на сходимость или расходимость этого ряда. Иными словами, если сходится ряд

, (1.21)

то сходится и ряд

. (1.22)

(но сумма может быть другой). И наоборот, если сходится ряд (1.22), то сходится и ряд (1.21).

Замечание 1. В математике термин «несколько» означает «конечное число», т.е. это может быть и 2, и 100, и 10¹⁰⁰, и больше.

Замечание 2. Из данного свойства следует, что ряды с общими членами и эквивалентны в смысле сходимости. Например, гармонический ряд имеет общий член , и ряды с общими членами и  также гармонические.

4. Остаток ряда. Его свойство. Если у ряда отбросить первые k членов, то получится новый ряд, называемый остатком ряда после k-го члена.

Определение. k-м остатком ряда

называется ряд

(1.23),

полученный отбрасыванием первых k членов исходного ряда.

Индекс k означает, сколько первых членов ряда отброшено. Таким образом,

и т.д.

М

Рис.1.5.2

ожно построить последовательность остатков и исследовать её на сходимость при , в отличие от предыдущей теоремы, где к бесконечности стремилось п. В каждом последующем члене этой последовательности «меньше» слагаемых (на самом деле в каждом остатке их бесконечное число). Можно также сказать, что здесь имеет место динамика в начале ряда, а не в его конце.

О

статок ряда можно определить также как разность между суммой ряда и его частичной суммой (рис.1.5.1):

. (1.24)

Н

Рис.1.5.2

айдём предел последовательности для сходящегося ряда с суммой S при . Из определения суммы ряда следует:

.

Тогда из (1.24) следует:

. (1.25)

Получили, что остаток сходящегося ряда есть величина бесконечно малая при , т.е. когда число отбрасываемых членов ряда стремится к бесконечности. Это видно и из рисунков 1.5.1 и 1.5.2.

Замечание. Теорему об отбрасывании нескольких членов ряда можно сформулировать следующим образом: для того, чтобы ряд сходился, необходимо и достаточно, чтобы его остаток стремился к нулю.