Тема 3 Наращение и дисконтирование с использованием схемы сложных процентов
Если инвестиция сделана на условиях сложного процента, то очередной годовой доход исчисляется не с исходной величины инвестируемого капитала, а с общей суммы, которая включает также ранее начисленные, но не востребованные инвестором проценты. В этом случае имеет место капитализация процентов по мере их начисления, так как база, с которой начисляются проценты, все время возрастает.
Таким образом, на протяжении срока финансовой операции размер инвестированного капитала будет равен:
к
концу первого года:
;
к
концу второго года:
;
и так далее …
к
концу n-го
года:
Это
равенство называется формулой наращения
по сложным процентам;
множитель
- множителем наращения сложных процентов;
- коэффициентом наращения.
Согласно формулы сложных процентов приращение капитала составит:
.
Формула наращения по сложным процентам является одной из базовых формул в финансовых вычислениях, поэтому для удобства пользования составлены специальные таблицы для определения в зависимости от изменения значений r и n. В этом случае формула алгоритма наращения по схеме сложных процентов трансформируется следующим образом:
где
–
мультиплицирующий множитель.
Экономический
смысл множителя
состоит
в следующем: он показывает, чему будет
равна одна денежная единица через n
периодов при заданной процентной ставке
r.
Рассмотренная формула предполагает, что измеряется в годах, а является годовой процентной ставкой. Однако эту формулу можно применять и при других периодах начисления. Необходимо только следить за соответствием длины периода и процентной ставки. Так, если базовым периодом начисления процентов является квартал (месяц), то и в расчетах должна использоваться квартальная (месячная) ставка.
Как и в случае начисления простых процентов, финансовое соглашение может предусматривать плавающие процентные ставки и при наращении по сложным процентам.
Пусть
- следующие друг за другом временные
периоды и на период
установлена процентная ставка
Тогда,
учитывая капитализацию начисленных
процентов при использовании схемы
сложных процентов, наращенная сумма за
время
определяется по формуле:
Обозначим
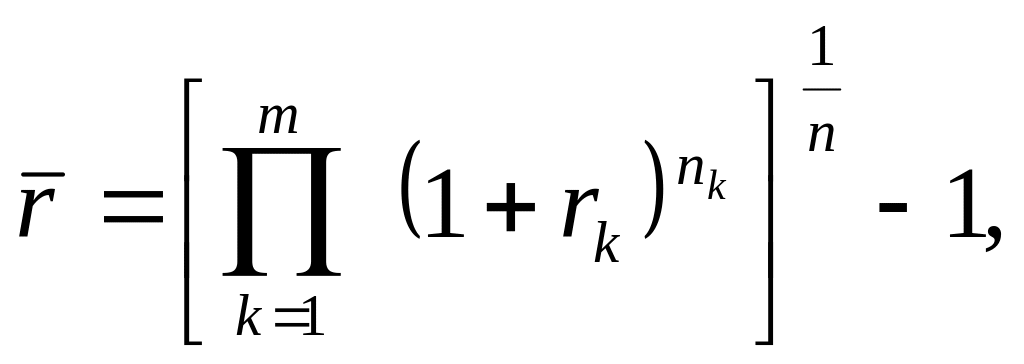тогда формула для определения наращенной
стоимости примет вид:
Таким
образом, в течение всего периода
финансовой операции можно установить
сложную ставку
,
приводящую к такому же результату,
как и с использованием переменных
ставок.
Пример. Предприниматель получил в банке ссуду в размере 40 тыс. грн. сроком на 7 лет на следующих условиях: для первого года процентная ставка равна 15% годовых, на следующие два года устанавливается маржа в размере 0,8% и на следующие годы маржа равна 0,9%. Найти сумму, которую предприниматель должен вернуть в банк по окончании срока ссуды.
тыс.грн.
Такая же величина наращенной суммы получится, если в течение 6 лет проценты будут начисляться по средней процентной ставке за весь период финансовой операции.
или
10,48%.
тыс.
грн.
Достаточно часто заключаются финансовые контракты, продолжительность которых отличается от целого числа лет.
В этом случае проценты могут начисляться с помощью следующих двух методов:
по схеме сложных процентов:
по смешанной схеме (используется схема сложных процентов для целого числа лет и схема простых процентов для дробной части года):
где w - целое число лет;
f - дробная часть года.
Пример. Банк предоставил ссуду в размере 50 тыс. грн. на 42 мес. под 16% годовых на условиях ежегодного начисления процентов. Какую сумму предстоит вернуть банку по истечении срока?
По схеме сложных процентов:
тыс.
грн
По смешанной схеме:.
тыс.
грн.
Таким образом, в данном случае смешанная схема приводит к большей величине наращенной суммы.
При проведении финансовых операций важно знать, как соотносятся между собой величины сумм, наращенных по схеме простых и схеме сложных процентов.
Для
ответа на этот вопрос сравним множители
наращения по простым и сложным процентам,
т.е. сравним
и
.
Очевидно, что при n=1
эти множители совпадают и равны 1+r.
Для любых значений n
справедливы следующие неравенства:
1)
,
если
2)
,
если
Таким образом, в случае ежегодного начисления процентов для лица, предоставляющего кредит:
более выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода);
более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно);
обе схемы дают одинаковый результат при продолжительности периода 1 год и однократном начислении процентов.
При заключении финансовых контрактов зачастую необходимо определить время, которое необходимо для увеличения первоначальной суммы PV в k раз при заданной доходности r в случае использования схемы простых и схемы сложных процентов:
для
простых процентов из равенства
получаем
:
для
сложных процентов из равенства
получаем
Из
этих формул можно, например, найти
период, за который происходит удвоение
капитала при заданной процентной ставке.
Полагая k=2,
соответственно получим:
для простых процентов, и
.
В практических расчетах при заключении финансовой сделки для быстрой оценки эффективности предлагаемой ставки процентов при реализации схемы сложных процентов зачастую пользуются приблизительным расчетом периода времени, необходимого для удвоения инвестируемой суммы. С этой целью используются несколько эмпирических приближенных формул:
«правило 72». Суть правила заключается в том, что, если – r процентная ставка, выраженная в процентах, то n представляет собой число периодов, за которое исходная сумма приблизительно удвоится. Здесь необходимо обратить внимание на то обстоятельство, что, если в большинстве финансовых расчетов используется процентная ставка, выраженная десятичной дробью, то в алгоритме формулы «правило 72» ставка взята в процентах.
«правило
69». Алгоритмом вычисления удвоенной
суммы в данном случае является
.
Заметим, что, как и в предыдущем правиле,
размер процентной ставки выражается в
процентах.
При использовании этих правил необходимо помнить, что при их применении речь идет о периодах начисления процентов и соответствующей данному периоду ставке. Например, если длительностью финансовой операции является половина года, то в расчете должна использоваться полугодовая процентная ставка.
Пример. Необходимо определить период времени, в течение которого исходный инвестированный капитал удвоится при процентной ставке, равной 17% годовых.
«правило
72» :
лет.
«правило
69» :
года.
точная
формула:
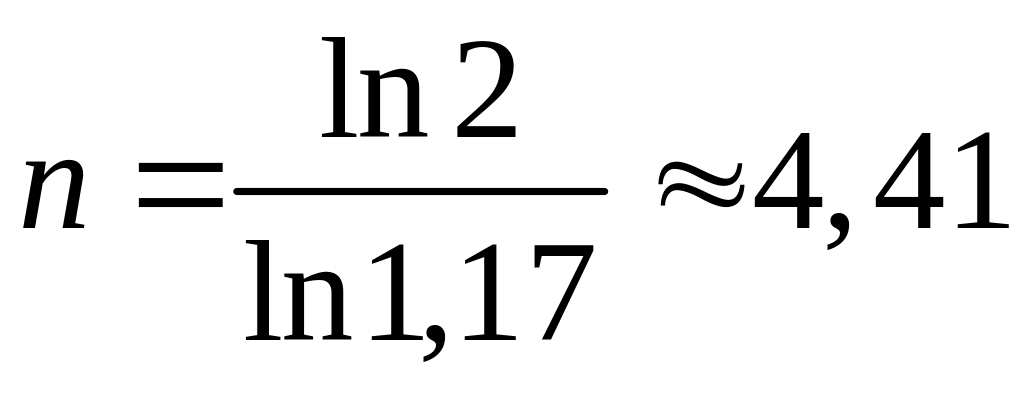года.
Как показывает практика, вышерассмотренные правила хорошо срабатывают для небольших значений процентной ставки, где-то до 20%.
Внутригодовые процентные начисления.
В практике финансовых соглашений часто встречаются ситуации, когда капитализация процентов происходит несколько раз в году – по полугодиям, ежеквартально, ежемесячно и даже ежедневно. Это может иметь место при заключении депозитных договоров, при получении банковского кредита, в акционерных обществах при выплате дивидендов и т.п.
В этом случае формула для нахождения наращенного капитала за n лет при m –кратном начислении процентов в год имеет следующий вид:
где n – количество лет финансовой операции;
m – количество начислений процентов в год;
r – годовая процентная ставка.
Пример.
В банк вложены деньги в сумме 5 тыс. грн. на два года с полугодовым начислением процентов под 20% годовых.
тыс.
грн.
Пример. В условиях предыдущего примера проанализирвать, изменится ли величина капитала к концу двухлетнего периода, если проценты будут начисляться ежеквартально.
тыс.
грн.
Из приведенных примеров можно сделать два простых практических вывода:
при начислении сложных процентов 12% годовых не эквивалентны 1% в месяц;
чем чаще идет начисление по схеме сложных процентов, тем больше накопленная сумма.
В зависимости от частоты начисления процентов, наращение суммы осуществляется различными темпами, причем с возрастанием частоты начисленная сумма увеличивается. Максимально возможное наращение осуществляется при бесконечном дроблении годового интервала.
Что же касается темпа прироста накопленной суммы, то с ростом частоты начисления процентов она постепенно уменьшается.
Пример.
Рассчитать накопленную сумму для различных вариантов начисления сложных процентов за один год, если исходная сумма равняется 1000 грн. а годовая процентная ставка 10%.
Частота начисления |
Наращенная сумма |
Наращение базисное |
Наращение цепное |
Ежегодное |
1100,00 |
- |
- |
Полугодовое |
1102,50 |
+2,5 |
+2,5 |
Квартальное |
1103,81 |
+3,81 |
+1,31 |
Ежемесячное |
1104,71 |
+4,71 |
+0,90 |
Ежедневное |
1105,17 |
+5,16 |
+0,45 |
При заключении финансовых контрактов возможны случаи, в которых начисление процентов осуществляется по внутригодовым подпериодам и продолжительность общего периода действия контракта не равна целому числу подпериодов. В этом случае также возможно использование двух схем:
схема
сложных процентов:
2)
по смешанной схеме:
где: – годовая процентная ставка;
- количество начислений в году;
-
целое число подпериодов в
годах;
–
дробная
часть подпериода.
Пример.
Банк предоставил ссуду в размере 120 тыс. грн. на 27 месяцев под 16% годовых на условиях единовременного возврата основной суммы долга и начисленных процентов. Проанализировать, какую сумму предстоит вернуть банку при различных вариантах и схемах начисления процентов: а) годовое; б) полугодовое; в) квартальное.
Годовое начисление процентов.
схема
сложных процентов:
тыс.
грн.
смешанная
схема:
тыс.
грн.
Полугодовое начисление процентов.
В этом случае мы имеем дело с ситуацией, когда начисление процентов осуществляется по внутригодовым подпериодам, а продолжительность общего периода действия контракта не равна целому числу подпериодов. Значит, решаем задачу с параметрами:
;
;
;
схема
сложных процентов:
тыс.
грн.
смешанная
схема:
тыс.
грн.
Квартальное начисление процентов.
В
этом случае параметры задачи:
;
;
,
т.е. продолжительность ссуды равна
целому числу подпериодов. Поэтому обе
схемы дают один и тот же результат:
тыс.
грн.