58 Линейные дифференциальные уравнения первого порядка

Линейным уравнением первого порядка называют уравнения вида

(1)

где - заданные функции независимого переменного x, определенные на некотором интервале .

Существуют несколько методов решения этого уравнения.

Метод вариации произвольной постоянной (метод Лагранжа).

Сначала решаем однородное уравнение

методом разделения переменных

или , где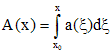

Тогда все решения уравнения (1) определяются формулой

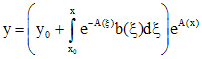
Метод Бернулли.

Решение уравнения (1) ищем в виде .  Подставляем данное выражение в (1),решением которого является функция

,

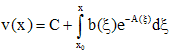где - произвольная постоянная.  Перемножая , получим (3).

59 Однородные ду первого порядка

Определение 1. Функция  называется однородной функцией

n-го измерения относительно переменных x и y, если при любом λ справедливо тождество

.

Например, функция  

Определение 2. Уравнение первого порядка называется однородным относительно x и y, если функция  есть однородная функция нулевого измерения относительно x и y.

Эти частные решения имеют вид

,

которые называются особыми решениями.

60 Ду, допускающие понижение порядка.

Уравнение ,                                                    (1)

где x - независимая переменная, y - искомая функция, а функция F определена и непрерывна в некоторой области и во всяком случае зависит от , называется обыкновенным дифференциальным уравнением n -го порядка.

Рассмотрим некоторые типы уравнений высших порядков, допускающие понижение порядка.

1. Уравнения, не содержащие искомой функции и нескольких последовательных производных. Рассмотрим уравнения вида .      (2)                                   

С помощью замены , где u  - новая неизвестная функция,  уравнение (2) приводится к уравнению (n-k) -го порядка: .

2. Уравнения, не содержащие явно независимой переменной.

Рассмотрим уравнения вида .                            (3)

С помощью замены .

Данная подстановка дает уравнение (n-1) - го порядка относительно новой неизвестной функции p:

3. Уравнения, однородные относительно .

Рассмотрим уравнения вида ,                    (4)

где F является однородной с показателем m относительно , т.е.

.

С помощью замены , где u - новая неизвестная функция, порядок уравнения (4) понижается на единицу. Имеем , , .

Данная подстановка дает дифференциальное уравнение (n-1) - го порядка относительно новой неизвестной функции u: .

4. Обобщенно - однородные уравнения.

Рассмотрим уравнения вида

.                                                                (5)

Уравнение (5) называется обобщенно - однородным, если существуют числа k и m такие, что .

Подстановка последних равенств ,дает уравнение вида ,

которое явно не содержит независимую переменную t.