42. Приложения вычислений определенного интеграла ( вычисление площади плоской фигуры, объема тела вращения, длины кривой).

1. Вычисление площадей плоских фигур.

Площадь криволинейной трапеции, расположенной «выше» оси абсцисс , равна соответствующему определенному интегралу:

или

 Пусть криволинейная трапеция ограничена линиями , х = а, х = b, у = 0 . Для нахождения площади S этой трапеции проделаем следующее:

1.Возьмем произвольное и будем считать,что S = S(x).

2.Дадим аргументу х приращение .

Функция S = S(x) получит приращение , представляющее собой площадь «элементарной криволинейной трапеции». Дифференциал площади dS -главная часть приращения  при , и он равен площади прямоугольника с основанием dx и высотой 

3.Интегрируя полученное равенство в пределах от х = а до х = b,получаем Если криволинейная трапеция расположена «ниже» оси Ox, то есть , то ее площадь может быть найдена по формуле _: Площадь фигуры, ограниченной кривыми  и , прямыми х = а и х = b (при   ) можно найти по формуле

.

2.Вычисление объема тела вращения

Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией , отрезком прямыми х = а и х = b. Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох ( ), есть круг с радиусом . Следовательно, S(x) = . Применяя формулу объема тела по площади параллельных сечений, получаем:

Если криволинейная трапеция ограничена графиком непрерывной функции и прямыми х=0, у=с, у = d (с < d), то объем тела, образованного вращением этой трапеции вокруг оси Оу), равен:

3. Определение длины дуги

Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у = f(х), где .

Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина ее наибольшего звена стремиться к нулю. Покажем, что если функция у=f(х) и ее производная у' = f'(x) непрерывны на отрезке [а;b], то кривая АВ имеет длину, равную

Применим схему I (метод сумм).1. Точками разобьем отрезок [а;b] на п частей. Пусть этим точкам соответствуют точки  на кривой АВ. Проведем хорды , длины которых обозначим соответственно через . Получим ломаную , длина которой равна

57. Дифференциальные уравнения 1 порядка, задача Коши.

Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида

F(x, y, y' )=0,     

где F — известная функция трех переменных, определенная в области G из R³,   x — независимая переменная из интервала (a, b), y(x) — неизвестная функция, y'(x) — ее производная.  

Обыкновенные дифференциальные уравнения, разрешенные относительно производной, т.е. уравнения вида 

y'=f(x, y)

называют уравнениями в нормальной форме.

Задача Коши. Заключается в нахождении решения u (x, t); х = (x₁,..., x_n) дифференциального уравнения вида:

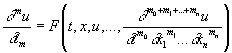, (1)

 m₀ < m, m > 0,

удовлетворяющего т. н. начальным условиям.

, t = t₀, x Î G₀, k = 0, …, m-1, (2)

где G₀ — носитель начальных данных — область гиперплоскости t = t_o пространства переменных x₁,..., x_n. Когда F и f_k, k = 0,..., m — 1, являются аналитическими функциями своих аргументов, задача Коши (1), (2) в некоторой области G пространства переменных t, х, содержащей G₀, всегда имеет и притом единственное решение. Однако это решение может оказаться неустойчивым (т. е. малое изменение начальных данных может вызвать сильное изменение решения), например в том случае, когда уравнение (1) принадлежит эллиптическому типу.