Решение

Методика построения плана ускорений до точки “c₃” включительно ана­логична описанной в примере 1. Поэтому приведем только необходимые вы­числения, векторные равенства, пропорции и краткие пояснения к построениям.

1. Определим ускорение точки A₁

= 15² · 0,096 = 21,6 м/с².

Вектор направлен вдоль AO от точки А к точке О.

2. Определим ускорение точки A₃. Составим векторные равенства ( 13 и 14):

;

,

где = 2 · 3,8 · 0,98 ≈ 7,45 м/с²;

= 3,8² · 0,280 ≈ 4 м/с².

Направление вектора определим с помощью плана скоростей (рис. 7, б). Вектор параллелен BD; вектор перпендикулярен BD; вектор параллелен BD и направлен от точки А к точке В.

3. Определим масштабный коэффициент плана ускорений.

Примем = 108 мм и по формуле (15) вычислим

= 21,6 / 108 = 0,2 [(м/с²)/мм].

Определим длины векторов, изображающих на плане ускорений и :

= 7,45 / 0,2 = 37 мм;

= 4 / 0,2 = 20 мм.

4. На основании равенств (13) и (14) проведем построения:

◊ из произвольного полюса π проведем луч, параллельный АО в направлении

вектора ; отложим на нем отрезок πa₁= 108 мм (рис. 12, б);

◊ из точки “a₁” проведем луч, перпендикулярный ВС в направлении

(см. рис. 7, б) и отложим на нем отрезок a₁k₁ = 37 мм;

◊ из точки “π ” проведем луч, параллельный ВС в направлении вектора

(то есть в направлении от А к В), и отложим на нем отрезок πn = 20 мм;

◊ через точку “k₁ ” проведем прямую, параллельную ВС (это линия действия вектора ), а через точку n – прямую, перпендикулярную ВС

(это линия действия вектора ). На их взаимном пересечении получим

точку “a₃”; соединив ее с полюсом π, получим вектор – ускорение

точки А₃ кулисы в масштабе μ_a.

5. Определим ускорения точек C₃ и D; составим пропорции для плана ускорений:

= BC / BA;

= BD / BA.

Откуда получим

,

.

где длина отрезка = 41 мм получена измерением на плане ускорений (рис.12, б); длины отрезков BA = 70 мм и BC = 99 мм получены измерениями на плане положения механизма (рис. 12, a); длина отрезка BD = 115 мм получена вычислением при построении плана положения механизма.

Так как на плане положения механизма точки А₃, C и D расположены по одну сторону от оси вращения В, то и на плане ускорений точки ”a₃” “с₃” и "d" должны быть расположены также по одну сторону от полюса π. Следова­тельно, точки “с₃” и "d" лежат на продолжении πa₃. В соответствии с этим на продолжении луча πa₃ отложим отрезки πс₃ = 58 мм и πd = 67 мм (рис. 12, б).

6. Определим ускорение точки C₅ ; составим векторное равенство:

, (20)

где .

Направление вектора определим с помощью плана скоростей

(рис. 7, б), повернув на по ω₃ вектор ; вектор параллелен BD; вектор параллелен оси (x – x₁), так как точка C₅ принадлежит рейке 5.

Вычислим: = 3,65 / 0,2 = 18 мм.

8. На основании равенства (20) из точки “c₃” проведем луч, перпенди­кулярный BD в направлении ; отложим на нем отрезок c₃k₂ =18 мм; че­рез точку “k₂” проведем прямую, параллельную BD (это линия действия век­тора ), а через полюс π – горизонтальную прямую. На их взаимном пересе­чении получим точку “c₅”.

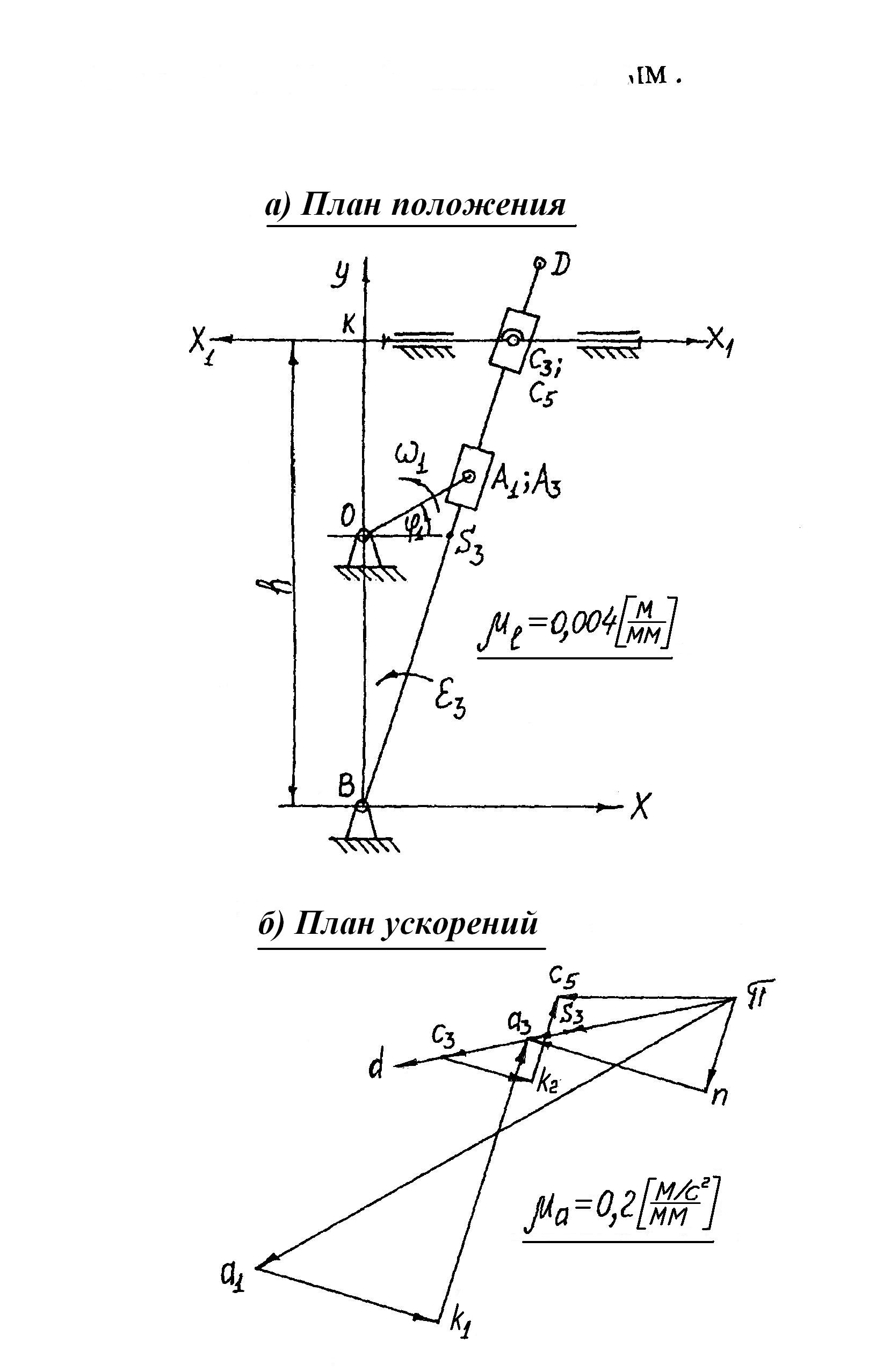
Рис. 12

9. Используя масштабный коэффициент μ_a, вычислим:

◊ ускорение точки C₅:

;

◊ ускорение центра масс S₃ кулисы BD:

м/ с²;

◊ угловое ускорение кулисы BD:

рад/с²,

где длина отрезка πc₅ = 34 мм получена измерением на плане ускорений;

l_AB = BA·μ_l = 70 · 0,004 = 0,28 м; длина отрезка ВА = 70 мм получена измере­нием на плане положения механизма (рис. 12, а).

Пример 4. Построим план ускорений (рис. 13, б) механизма подачи суппорта долбежного станка. Схема механизма изображена на рис. 13, а.

Для решения задачи необходимо предварительно построить план поло­жения и план скоростей механизма.

План положения механизма построен на рис. 13,а. План скоростей меха­низма построен на рис. 13, б. Методика этих построений была рассмотрена в параграфах 1.1 и 1.2.

Исходные данные: ; ; ; ; ; ;

По плану скоростей (рис. 8, б) определили:

; ; .

Методика построения для кулисной части механизма (звенья 1, 2 и 3) описана в примере 2. Поэтому приведем только необходимые вычисления, век­торные равенства, пропорции и краткие пояснения к построениям.

1. Определим ускорение очки A₁

;

вектор направлен вдоль AO (см. рис. 13, а);

2. Определим ускорение точки A₃. Составим векторные равенства (13) и (14):

;

,

где ;

;

;

направление вектора определим, используя план скоростей (рис. 8, б); век­тор параллелен BE; вектор перпендикулярен BE; вектор на­правлен вдоль BE (см. рис. 13, а);

3. Определим масштабный коэффициент плана ускорений.

Примем = 106 мм и по формуле (15) вычислим

= 10,58 / 106 ≈ 0,1 [(м/с²)/мм].

Определим длины векторов, изображающих на плане ускорений и :

;

4. На основании равенств (13) и (14) проведем построения:

◊ из произвольного полюса π проведем луч, параллельный АО в направлении

вектора ; отложим на нем отрезок πa₁= 106 мм (рис. 13, б);

◊ из точки “a₁” проведем луч, перпендикулярный ВС в направлении

(см. рис. 8, б) и отложим на нем отрезок a₁k = 40 мм;

◊ из точки “π ” проведем луч, параллельный ВС в направлении вектора

и отложим на нем отрезок πn₁ = 23 мм;

◊ теперь через точку “k” проведем прямую, параллельную ВС (это линия дей­ствия вектора ), а через точку n₁ – прямую, перпендикулярную ВС

(это линия действия вектора ). На их взаимном пересечении получим

точку “a₃”; соединив ее с полюсом π, получим вектор – ускорение

точки А₃ кулисы в масштабе μ_a.

5. Определим ускорения точек E, S₃ и C; составим пропорции для плана ус­корений:

πe / πa₃ = BE / BA; πs₃ / πa₃ = BS₃ / BA; πc / πa₃ = BC / BA;

откуда получим:

;

;

πc = πa₃·BC / BA = 36·40/85 ≈ 17 мм,

где длина отрезка = 36 мм получена измерением на плане ускорений (рис.13, б); длина отрезка BA = 85 мм получена измерением на плане положения механизма (рис. 13, a); длины отрезков BE = 112 мм, BS₃ = 36 мм и BC = 40 мм получены вычислением при построении плана положения механизма (см. § 1.2, пример 4).