4. Форсирующее звено 2-го порядка

ПФ:

При k=1 ЛЧХ – зеркальные отображения ЛЧХ колебательного звена относительно оси частот.

Форсирующие звенья как первого, так и второго порядка физически неосуществимы.

4. Минимально-фазовые звенья

В общем случае ;

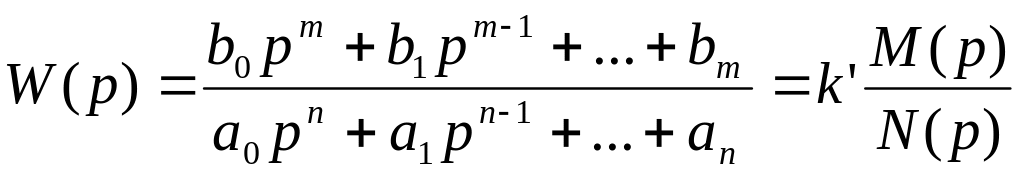где

k’=b0/a0 - приведенный коэффициент усиления;

; ;

.

Это приведенные многочлены (коэффициент при старшем члене равен 1).

По теореме Безу:

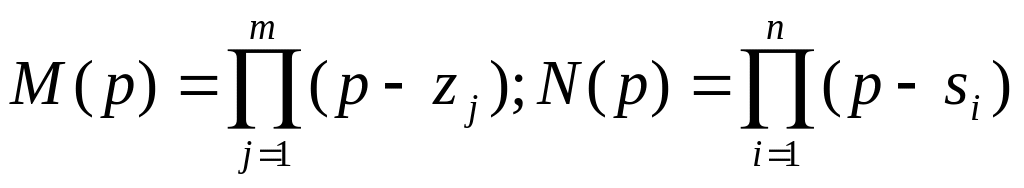
Здесь zj, - нули ПФ; si, - полюса ПФ.

Как видим, M(p) и N(p) – приведенные многочлены.

zj находятся как корни M(p)=0; W(p)=0

si - находятся как корни N(p)=0; W(p)=

Если N и M не содержат общих множителей, то говорят, что zj и si - нули и полюса звена.

Определение. 1.Звено называется минимально-фазовым, если вещественные части всех его нулей и полюсов являются отрицательными или тождественно равными нулю.

2. Звено называется неминимально-фазовым, если оно содержит хотя бы один нуль или полюс с положительной вещественной частью.

Условие минимальной фазности:

Re Si≤0, , Re Zj≤0,

Неминимально-фазовые звенья, содержащие полюсы с положительной вещественной частью называются неустойчивыми звеньями.

Пример. Рассмотрим апериодическое звено с ПФ: , Т>0

Следовательно, имеет полюс S1=-1/T <0 – минимально-фазовое звено.

Рассмотрим неустойчивое апериодическое звено с ПФ: ;

S1=1/T >0 – неминимально-фазовое звено.

ЛАЧХ: L(w)=La(w) ; L(w) – неустойчивого, La(w) – апериодического.

ФЧХ: (w)=-[π+ a(w)], где а(w)=-arctg wT (1)

| (w)|>| a(w)|, , кроме

w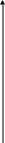

а(w)

(w)

-π

-π/2

0

К минимально-фазовому звену из множества звеньев с одинаковыми ЛАЧХ, относится 1 звено с ФЧХ (1)

Выражение для ФЧХ минимально-фазового звена по теореме Бодэ

(w)= , (*)

где =lg w.

Из этого выражения следует, что для минимально-фазового звена:

1. можно найти (w) по L(w);

2. выражение (w) для ФЧХ при =lg w в основном определяется наклоном L(w), т.к. - малая величина.

Условие минимальной фазности позволяет находить W(p) по L(w), и по W(p) находить (w), особенно просто по асимптотической ЛАЧХ.

Пример. Известна ЛАЧХ минимально-фазового звена. Надо найти W(p).

La

-20

w

0

5

20

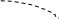
Так как 20lgk=20, а следовательно, k=10; 1/T=5, поэтому T=0.2.

ПФ W(p)=10/(0.2p+1), т.к. звено минимально-фазовое. Отсюда ЛФЧХ

(w)=-arctg0.2w.

3. Описание сау

Математической моделью САУ является ДУ, связывающее управляемую величину и внешние воздействия.

1. Понятие о структурной схеме.

Систему можно описать с помощью уравнений связи и уравнений звеньев.

Пусть система включает N звеньев и известны уравнения звеньев системы в изображениях, представленные в виде Yi(p)=Wi(p)Vi(p) (1), ,

Yi(p) и Vi(p) – выходные и входные величины i-го звена, а Wi(p)=Yi(p)/Vi(p) – ПФ i-го звена.

В простейшем случае уравнение связи имеет вид: V2(p)=Y1(p) – вход 2гозвена равен выходу 1-го. Более сложный случай:

(*)

В (*) V4(p) – вход 4-го звена, - внешнее воздействие на вход 4-го звена, Y1(p), Y3(p), Y5(p) – выходные сигналы 1-го, 3-го, 5-го звеньев.

В общем случае уравнение связи для i-го звена:

, (2)

где - числовые коэффициенты, определяемые как:

0, если связь между входом i-го и выходом j-го звена отсутствует

= 1, если связь между входом i-го и выходом j-го звена является положительной

-1, если связь между входом i-го и выходом j-го звена является отрицательной

Если =1 – то говорят, что i-ое звено охвачено положительной обратной связью (ПОС)

Если =-1 – то говорят, что i-ое звено охвачено отрицательной обратной связью (ООС)

Внешние воздействия: возмущающее воздействие f(p), шум наблюдения S(p), V(p) – задающее воздействие, например, .

Уравнения (1) и (2) дают полное описание САУ, но часто их дополняют уравнением для Y(p) – уравнением выхода, например, Y(p)=YN(p).

Определение. Графическое отображение уравнений звеньев (1) и уравнений связи (2) называется структурной схемой САУ (графическая модель системы).

Структурная схема включает в себя 3 элемента:

1) динамическое звено, отображает уравнение каждого звена, входящего в систему

Wi(p)

Vi(p)

Yi(p)

Это соответствует

Yi(p)=Wi(p)Vi(p),

Wi(p) – ПФ i-го звена

2) элемент суммирования: V3(p)=V1(p)±V2(p). Изображается кружком с перекрестием.

V2(p)

±

V1(p) +

V3(p)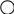

3) точка разветвления сигнала (точка съема)

«а» - точка съема

V

V

‘a’

y

Зная уравнения (1) и (2) можно построить структурную схему. Но схема – не самоцель. (1) и (2) – система алгебраических уравнений, с помощью которой можно определить любую переменную Yi(p), через изображения внешних воздействий ,

или ,

Для получения уравнения САУ используют преобразования структурных схем, т.е. соединения звеньев заменяют одним звеном с эквивалентной ПФ. Проводя несколько раз подобную операцию, приходят к простому соединению звеньев.

Правила преобразования схем.

1. Последовательное соединение - это соединение, при котором выходная величина каждого предыдущего звена является входом последующего. Рассмотрим соединение двух звеньев N=2: y1=W1V1; y2=W2V2 (3);

V=V1; y1=V2; y2=y. Найдем W – ПФ звена, эквивалентного последовательному соединению.

; W1=y1/V1; W2=y2/V2;

W1

W2

V=V1

y1=V2

y2=y

W=W1*W2

W=W1*W2*…*Wn=

2. Параллельное соединение – входная величина поступает на несколько звеньев, а выходные сигналы суммируются.

Пусть 2 звена описываются уравнением (3), а уравнения связи V=V1=V2, уравнение выхода y=y1+y2.

ПФ: W=y/V=(y1+y2)/V=y1/V + y2/V=W1+W2

W=W1+W2

W=W1+W2+…+Wn=

3. Соединение звеньев с ОС.

Пусть 2 звена описываются уравнением (3). Уравнение связи V1=V(±)y2;

V2=y1=y; (-) – ООС; (+) – ПОС

W1 – ПФ прямой связи, W2 – ПФ обратной связи.

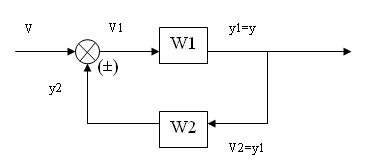
Если W2=1 - соединение звеньев с единичной ОС.

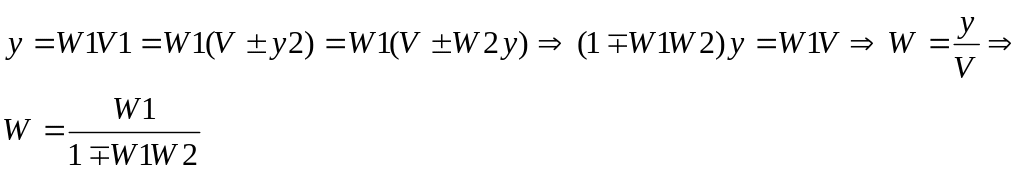
W – ПФ замкнутого контура.

Для получения ПФ разомкнутого контура разрывают ОС: получается последовательное соединение двух звеньев Wp=W1*W2 – ПФ разомкнутого контура.

4. Перемещение элементов суммирования.

а) на выход звена (по ходу сигнала)

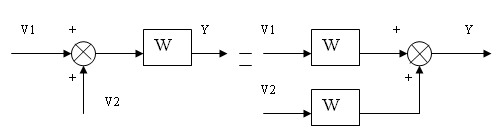
y=W(V1+V2)=WV1+WV2

б) на вход звена

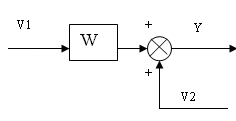
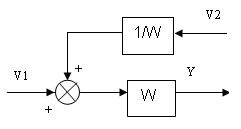
y=WV1+V2=W(V1+V2*1/W)

5. Перемещение точек съема.

а) на выход звена

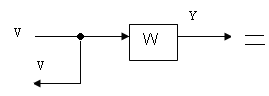
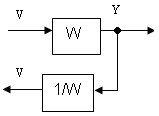
б) на вход звена

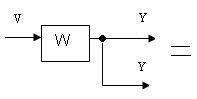
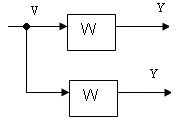
6. Перестановка элементов суммирования и точек съема

а) перестановка элементов суммирования

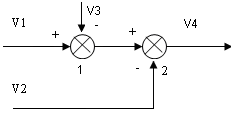
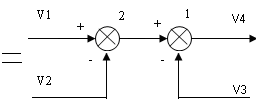
V4=(V1-V3)-V2=V1-V2-V3

б) перестановка точек съема

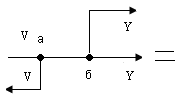
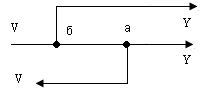
Алгоритм преобразования структурной схемы:

1) Развязать перекрещивающиеся контуры ОС (правила 4-6).

Рекомендация: как правило, переносят элементы суммирования против хода сигнала, а точки съема по ходу сигнала.

2) Заменить каждое из соединений звеньев одним звеном с эквивалентной ПФ (правило 1-3).

Пример: Трехконтурная структурная схема. Надо найти ПФ системы Ф=Y/V.

1. Переносим элемент суммирования 1 на вход звена W1, а затем меняем местами 1-ый и 2-ой элементы суммирования?

2. Переместим точку съема «а» на выход звена W4, а затем поменяем местами точки «а» и «б».

W8=W1*W2/(1+W1*W2*W5);

W9=W3*W4/(1+W3*W4*W6);

W10=W7/W1*W4

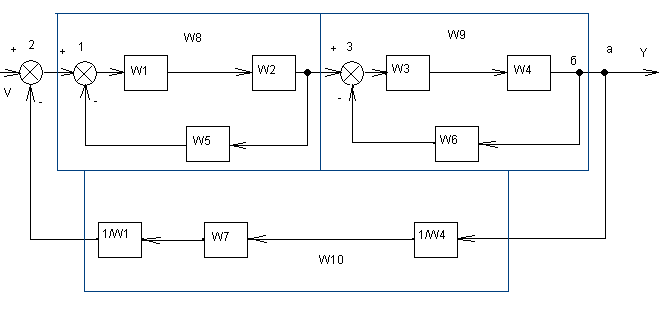
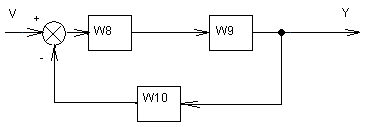
Ф=W8*W9/(1+W8*W9*W10)

Уравнения и ПФ одноконтурных САУ

1. Типовые структурные схемы замкнутой системы.

После преобразования структуры ОУ к одному звену выбирается закон управления, который определяет структурную схему системы управления. Рассмотрим типовые структурные схемы, соответствующие типовым законам управления.

А) Управление с прямой и обратной связью

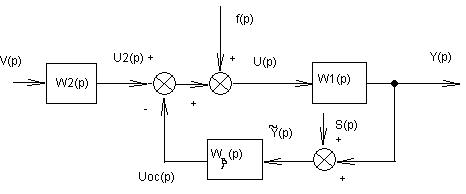
рис. 1 Типовая схема САУ с прямой и обратной схемой.

На этом рис. V(p) – изображение по Лапласу задающего воздействия V(t); f(p) - изображение по Лапласу возмущающего воздействия f(t), эквивалентного по своему влиянию нескольким возмущающим воздействиям, обычно действующим на САУ; S(p) - изображение по Лапласу шума измерения S(t); - изображение по Лапласу наблюдаемого сигнала ; Y(р) – изображение управляемой величины Y(t), причем обычно =Y(t)+S(t); U(p) – изображение управляющего воздействия (управления) V(t); W1(p) – ПФ ОУ.

Если положить f=S=0, то получаем закон управления (в изображениях) с прямой и обратной связью:

U(p)=W2(p)V(p)-W_β(p)Y(p),

описывающий работу управляющего устройства.

Здесь W2(p) – ПФ прямой связи (ПФ управляющего устройства по задающему воздействию), W_β(p) – ПФ ОС (ПФ управляющего устройства по выходной, управляемой величине).

Эта структурная схема соответствует системе с неединичной обратной связью.

Б) Управление по ошибке

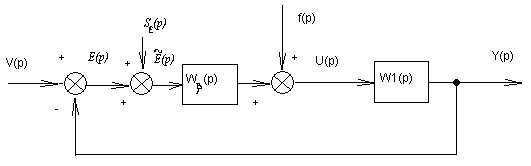
рис. 2

При этом структурная схема получается из схемы (рис. 1) при W2(p)= W_β(p), . Здесь - изображение ошибки управления . На выходе датчика ошибки (сравнивающего устройства) получаем сигнал ошибки

,

где - изображение шума измерения ошибки . Здесь закон управления (при ) описывается выражением:

U(p)= W_β(p)*

Такой закон называется законом управления по ошибке. Его удобно использовать тогда, когда не удается измерить задающее воздействие, а можно измерить разность V(t) и Y(t).

2. Передаточные функции замкнутой одноконтурной САУ.

На САУ влияет 3 внешних воздействия – задающее, возмущающее и шум измерения.

Поэтому различают 3 ПФ:

1) ПФ по задающему воздействию (ПФ замкнутой системы) – это отношение изображения по Лапласу управляемой величины предварительно невозбужденной системы к задающему воздействию в отсутствие других внешних воздействий.

Ф(р)= (1)

При f=S=0 структурная схема (рис. 1) принимает вид

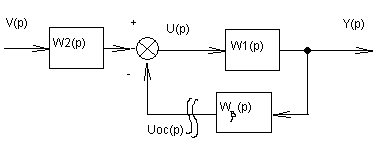
Используя правила преобразования структурных схем, находим ПФ по задающему воздействию.

ПФ разомкнутого контура ОС: Ф(р)=

Для рис. 1 W(p)=W1(p)*W_β(p) (*)

С учетом выражения (*) ПФ замкнутой системы по задающему воздействию можно записать так:

(2)

Структуру системы с единичной ОС, изображенной на рис. 2, при , легко преобразовать к виду, называемому структурой Блэка:

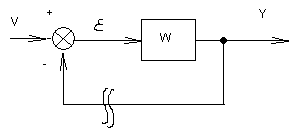
Здесь ПФ W определяется по (*) и называется ПФ разомкнутой системы. ПФ по задающему воздействию определяется в случае единичной обратной связи как

(**)

и называется передаточной функцией замкнутой системы.

Как видим, в этом случае ПФ замкнутой системы полностью выражается через ПФ разомкнутой системы.

Реакцию системы на отдельно взятое задающее воздействие часто обозначают с индексом v, т.е. в виде

y(p)=y_v(p).

2) ПФ по возмущающему воздействию (по возмущению) - это отношение изображения по Лапласу управляемой величины к возмущающему воздействию предварительно невозбужденной системы в отсутствие других внешних воздействий.

Согласно определения эта ПФ записывается так:

Ф_f(р)= (3)

Выразим Ф_f(р) через ПФ ОС и ПФ ОУ. С этой целью преобразуем структурную схему (рис. 1) к другому виду, считая входом f(p) и учитывая, что V=S=0.

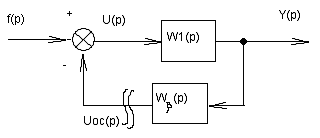
Также учитываем, что

U(p)=f(p)-U_oc(p)

Используя правило, относящееся к соединению звеньев с ОС, получаем

(4)

где W(p) определяется по выражению (*).

ПФ по возмущению для системы с единичной ОС не отличается от выражения (4).

Реакция системы на отдельно взятое возмущающее воздействие обозначается с индексом f, т.е. как

y(p)=y_f(p).

3) ПФ по шуму измерения - это отношение изображения по Лапласу управляемой величины к шуму измерения предварительно невозбужденной системы в отсутствие других внешних воздействий.

Формально ПФ по возмущению выглядит так:

Ф_s(р)= (5)

Считая входом системы шум измерения и учитывая отсутствие других внешних воздействий, преобразуем структуру, представленную на рис. 1, к следующему виду:

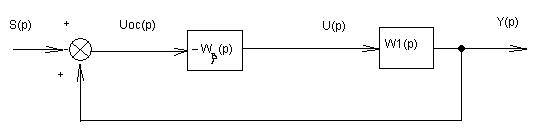
Используя выражения для ПФ соединения звеньев с положительной ОС, получаем или (6)

Для системы с единичной ОС ПФ по шуму измерения ошибки Ф_sε(р)= равняется ПФ замкнутой системы, т.е. Ф_sε(р)=Ф(р).

Реакция системы на отдельно взятый шум измерения обозначается как

y(p)=y_s(p).

Стандартная форма представления ПФ разомкнутой системы (контура).

W_i(p)=K_i(p)/D_i(p) – для i-го звена

ПФ разомкнутой системы W(p)=Y(p)/ε(p) вычисляется в результате алгебраических операций над ПФ звеньев, которые представляют собой отношение многочленов от р.

Следовательно, ПФ разомкнутой системы также можно представить в виде отношения двух многочленов W(p)=K(p)/D(p).

В теории управления принято представлять эту ПФ в стандартной форме, т.е. как

,

где - нормированная ПФ разомкнутой системы, удовлетворяющая условию W₀(0)=1; ν – число интегрирующих звеньев, входящих в ПФ. От числа интегрирующих звеньев зависит точность системы; k – коэффициент усиления разомкнутой системы (контура), определяемый выражением

Выясним физический смысл коэффициента усиления. Для этого используя выражение

найдем уравнение разомкнутой системы в изображениях.

Здесь представляет собой преобразование Лапласа от ν-той производной управляемой величины предварительно невозбужденной системы.

Пусть ошибка является постоянным сигналом ε(t)=ε₀=const, так что ее изображение ε(р)= ε₀/р. При этом установившееся значение ν-ой производной находим по теореме о конечном значении:

=

Отсюда, коэффициент усиления разомкнутой системы представляет собой отношение установившегося значения ν-ой производной ее реакции и постоянного входного сигнала:

Размерность k=[c^-ν]

Пример. Преобразуем ПФ к стандартному виду. Т.к. ν=1, то k=20с^-1 и

Реакция замкнутой системы на внешние воздействия.

Рассмотрим следующую задачу.

Дано: Передаточные функции предварительно невозбужденной замкнутой системы Ф(р); Ф_f(p); Ф_s(p) и математические модели внешних воздействий V(t); f(t); S(t).

Требуется найти реакцию замкнутой системы y(t).

Используя принцип суперпозиции (принцип наложения), согласно которому реакция линейной системы на несколько внешних воздействий, приложенных в разные точки структурной схемы, равна сумме реакций на каждое из внешних воздействий, взятых в отдельности, искомую реакцию можем записать как

y(t)=y_v(t)+y_f(t)+y_s(t).

Здесь y_v(t), y_f(t), y_s(t) – соответственно реакции замкнутой системы на отдельно взятые в отдельности задающее воздействие v(t), возмущающее воздействие f(t) и шум измерения s(t). Отсюда преобразование Лапласа у(р) реакции y(t) равняется сумме преобразований Лапласа y_v(р), y_f(р), y_s(р) реакций y_v(t), y_f(t), y_s(t), т.е.

y(р)=y_v(р)+y_f(р)+y_s(р).

В соответствии с (1), (3) и (5) преобразование реакции у(р)

У(р)=Ф(р)V(p)+Ф_f(р)f(p)+Ф_s(p)S(p) (7)

где ПФ замкнутой системы можно определить с помощью структурной схемы. Определяя обратное преобразование Лапласа от (7), находим y(t)=L^-1[y(p)]. В частности, используя теорему об изображении интеграла свертки, получаем реакции

где k(t)=L^-1[Ф(p)] – весовая функция замкнутой системы.

k_f(t) – весовая функция по возмущающему воздействию.

k_s(t) – весовая функция по шуму измерения.

Дифференциальные уравнения замкнутой системы.

ДУ системы – это уравнение, связывающее между собой y(t) c V(t), f(t), S(t). ДУ можно определить с помощью структурной схемы (рис. 1) по известным ПФ ее звеньев. Предположим, что найдены в виде отношения многочленов

- ПФ ОУ

- ПФ прямой связи

- ПФ ОС

При этом

1+W(p)=1+

где Д(р)= + (8)

В соответствии с (2), ПФ по задающему воздействию

(9)

В соответствии с (4) ПФ по возмущающему воздействию

(10)

В соответствии с (6) ПФ по шуму измерения

(11)

Если числители этих ПФ не содержат общих делителей со знаменателем Д(р), то Д(р) – характеристический многочлен замкнутой системы.

Пример. ; Д(р)= , а р+1≠Д(р)

Из (7) с учетом (9-11) после умножения на Д(р) получаем уравнение замкнутой системы в изображениях

Д(р)У(р)=К1(р)К2(р)V(р)+К1(р)D2(р)f(p)-К1(р)К_β(р)S(p) (12)

Если правая часть равна нулю, то Д(р)У(р)=0 – характеристическое уравнение замкнутой автономной системы в изображениях. Заменяя в (12) изображения сигналов оригиналами и многочлены от р операторными многочленами, получаем дифференциальное уравнение замкнутой системы, записанное в операторной (символической) форме

Д(D)У(t)=К1(D)К2(D)V(t)+К1(D)D2(D)f(t)-К1(D)К_β(D)S(t) (13)

D – оператор дифференцирования.

Пример. Пусть ПФ

, ,

S=0. В этом случае

K1(p)=k1; K2(p)=k₂(T₂p+1); =k₃(T₃p+1); D1(p)=T₁p+1; D2(p)=p

Согласно (8)

Д(р)= + =( T₁p+1)р+ k1k₃(T₃p+1)=T₁p²+(1+k1k3T₃)p+k₁k₃

В соответствии с (12) и (13) находим уравнение замкнутой системы в изображениях

[T₁p²+(1+k1k3T₃)p+k₁k₃]Y(p)=k1k2(T₂p+1)V(p)+k1pf(p)

в операторной форме

[T₁D²+(1+k1k3T₃)D+k₁k₃]y(t)=k1k2(T₂D+1)V(t)+k1Df(t)

и в оригиналах