6. Робастная устойчивость

Если модель системы точно не определена (обычный случай), то необходимо обеспечить, по меньшей мере, номинальную устойчивость. Все, что было до сих пор сказано об устойчивости, основано на предположении, что линеаризованная модель объекта точно описывает систему в окрестности состояния равновесия. Так как все реальные системы являются нелинейными, то удобно рассматривать саму линейную аппроксимацию (линеаризованную модель) системы как обладающую модельной неопределенностью, так что модель, которую мы приняли для исследования устойчивости, является лишь номинальной моделью объекта. Все методы анализа устойчивости, прямые или косвенные, при использовании номинальной модели гарантируют только номинальную устойчивость.

Робастная устойчивость имеет отношение к устойчивости для всех моделей в рамках (пределах) модельной неопределенности. Робастная устойчивость может быть в принципе гарантирована, если условия устойчивости соблюдаются для всех возможных моделей неточно определенной системы. К сожалению, при этом анализ устойчивости оказывается весьма затруднительным. Однако критерий Найквиста может быть использован для суждения о робастной устойчивости, если ввести в рассмотрение модельную неопределенность как частотную функцию (модельную неопределенность в частотной области), которая оценивает уровень модельной неопределенности для каждого значения частоты. В общем случае, как показала практика, неопределенность имеет тенденцию быть больше на высоких частотах и модуль АФХ разомкнутой системы может быть измерен точнее, чем ее аргумент (фаза).

С помощью критерия Найквиста можно определить робастную устойчивость. Число охватов критической точки (-1, j0) АФХ разомкнутой системы (диаграммой Найквиста) является решающим тестом в частотной области для ответа на вопрос о номинальной устойчивости. Если число охватов удовлетворяет условию номинальной устойчивости, расстояние от АФХ разомкнутой системы до критической точки (-1,j0) определяет робастную устойчивость в терминах модельной неопределенности в частотной области. Это расстояние |1+W(jw)| (см. рисунок ниже) обратно

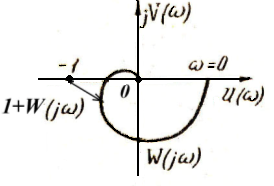
пропорционально модулю |S(jw)| так называемой функции чувствительности

S(jw)=1/[1+W(jw)].

Таким образом, малая чувствительность на данной частоте соответствует большему расстоянию от АФХ разомкнутой системы до критической точки (-1,j0) и отсюда высокой робастной устойчивости на этой частоте.

Запас устойчивости по модулю является мерой робастной устойчивости для частоты w_π, на которой ФЧХ разомкнутой системы равна -180 градусам. Этот запас есть количественная оценка робастной устойчивости при «чистом» отклонении (возмущении) модуля АФХ разомкнутой системы. В то время как запас устойчивости по фазе является количественной мерой робастной устойчивости для частот (они называются частотами среза w_с), на которых модуль АФХ разомкнутой системы принимает значения, равные единице. Этот запас есть количественная оценка робастной устойчивости при «чистом» отклонении (возмущении) фазы АФХ разомкнутой системы. Заметим, что замкнутая система с модулем АФХ (со значениями АЧХ), превышающим единицу в некотором диапазоне частот, имеет ограниченный запас устойчивости по фазе, что вытекает из критерия Найквиста. Никогда не забывайте, что расстояние от АФХ разомкнутой системы до критической точки (-1,j0) неуместно для использования, если число охватов не удовлетворяет критерию Найквиста, т.е. если номинальная устойчивость не имеет места. Вот почему непродуманное использование управляющего устройства с высоким коэффициентом усиления не может служить как жизнеспособная стратегия управления.

Запас устойчивости по фазе определяется следующим образом. На комплексной плоскости U, jV проводится окружность единичного радиуса с центром в начале координат (рис. 15) и отмечается точка ее пересечения с характеристикой W(jw). Угол γ, образуемый проходящим через эту точку радиусом и отрицательной частью вещественной оси, называется запасом устойчивости по фазе.

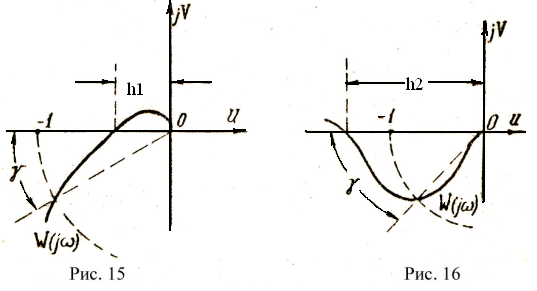
Запас устойчивости по амплитуде характеризует расстояние между критической точкой (-1,j0) и ближайшими точками пересечения характеристики W(jw) с вещественной осью. Если точка пересечения располагается справа от критической точки, то в качестве запаса устойчивости по амплитуде принимают величину 1/h1, обратную расстоянию от этой точки пересечения до мнимой оси (рис. 15).

Если АФХ имеет несколько пересечений отрицательной вещественной оси, то запас по модулю определяется по той точке, которая дает наименьшее значение 1/h.

Если же точка пересечения находится слева от точки (-1,j0), то под запасом устойчивости по амплитуде понимают расстояние h2 от точки пересечения до мнимой оси (рис. 16). Нетрудно видеть, что чем больше удалены точки пересечения характеристики W(jw) с вещественной осью от критической точки (-1,j0), тем больше запасы устойчивости 1/h1 и h2.

Для того, чтобы определить запасы устойчивости по логарифмическим частотным характеристикам, рассмотрим вид логарифмических частотных характеристик, соответствующих устойчивой и неустойчивой системам.

7. Логарифмический критерий устойчивости

Для проверки устойчивости замкнутой системы можно использовать также логарифмические частотные характеристики разомкнутой системы. Рассмотрим вначале ситуацию, когда каждая из логарифмических частотных характеристик лишь один раз пересекает ось частот.

1) Замкнутая система неустойчива

Для неустойчивой системы, которая устойчива в разомкнутом состоянии АФХ W(jw) приведена на рис. 17,a. Мы видим, что в данном случае значению фазы φ(w)=-180^о соответствует значение R(w) больше единицы, так что при этом L(w)=20lgR(w)>0.

a) б)

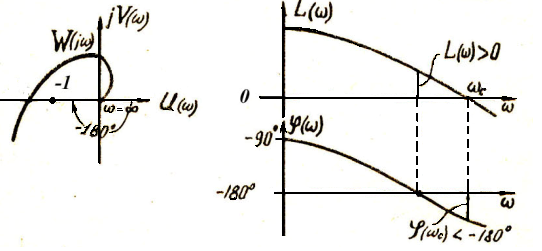
Рис. 17

Это является признаком неустойчивой замкнутой системы и соответствует взаимному расположению логарифмических частотных характеристик L(w) и φ(w), показанному на рис. 17, б.

Для удобства отсчета фазы ось абсцисс при построении логарифмической фазовой характеристики обычно проводят при значении φ(w)=-180^о.

2) Замкнутая система устойчивая

Из рассмотрения АФХ W(jw) устойчивой разомкнутой системы, которая в замкнутом состоянии неустойчивая, видим, что значению φ(w)=-180^о соответствует R(w)=1/h <1 (рис. 18,а). При этом

L(w)=20lgR(w)=-20lgh<0 (рис. 18,б). Это является признаком устойчивой замкнутой системы.

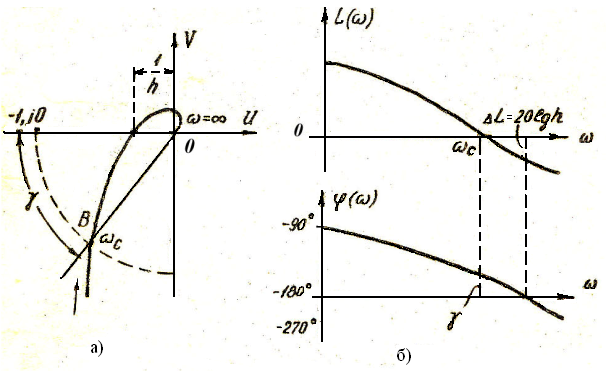
Рис. 18

Ордината L=20lgh характеристики L(w), соответствующая значению φ(w)=-180^о, определяет запас устойчивости по амплитуде, выраженный в децибелах. Рекомендуется иметь запас устойчивости по амплитуде не менее 10-15 дБ.

Угол γ, представляющий собой запас устойчивости по фазе, определяется точкой В, полученной в результате пересечения характеристикой W(jw) окружности единичного радиуса, проведенной из начала координат. Следовательно, в точке В величина R(w)=1, а это значит, что частота, соответствующая точке В, есть частота среза.

Таким образом, на логарифмических характеристиках угол γ представляет собой ординату фазовой характеристики, соответствующую частоте среза w_c (рис. 18б).

Замкнутая система будет находиться на колебательной границе устойчивости, если на той же частоте w_с, где ЛАЧХ разомкнутой системы обращается в нуль, значение фазовой частотной характеристики равно -180 градусов.

Общий случай. Будем считать «+1 – пересечением» логарифмической фазовой характеристикой уровня -180 градусов снизу вверх и «-1 – пересечением» - пересечение логарифмической фазовой характеристикой уровня -180 градусов сверху вниз при положительном значении логарифмической амплитудно-частотной характеристикой.

Логарифмический критерий устойчивости гласит: Если разомкнутая система имеет l правых полюсов, то для устойчивости замкнутой системы необходимо и достаточно, чтобы на интервале частот, когда L(w)>0, число пересечений фазовой характеристикой уровня -180 градусов снизу вверх превышало число пересечений сверху вниз на l/2. На рис. 18 показаны АФХ и соответствующие ей логарифмические характеристики.

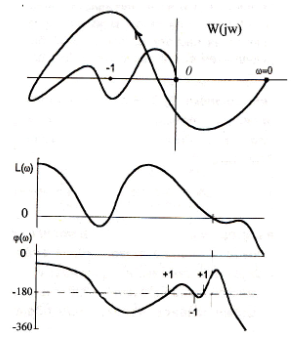
Рис. 18

Как видим, число пересечений снизу вверх(+1) равно 2, а число пересечений сверху вниз (-1) равно 1. Отсюда замкнутая система устойчивая, если разомкнутая система имеет l=2 правых полюсов.

8. Устойчивость систем управления с запаздыванием.

В предыдущих разделах критерий устойчивости Найквиста рассматривался применительно к системам, передаточные функции которых имели дробно-рациональный вид. Однако во многих системах управления присутствует запаздывание по времени, существенно влияющее на устойчивость. Запаздывание по времени – это промежуток времени между моментом, когда в каком-то месте системы произойдет некоторое событие, и моментом, когда это событие проявит себя в другом месте. Критерий Найквиста обладает тем преимуществом, что он позволяет учесть влияние этого запаздывания на устойчивость системы. Идеальное запаздывание по времени можно охарактеризовать передаточной функцией

W_d(p)=e^-pτ ,

где τ есть время запаздывания. Критерий Найквиста остается в силе и для систем с запаздыванием, поскольку множитель e^-pτ не приводит к появлению дополнительных полюсов или нулей в передаточной функции разомкнутой системы. Этот множитель, не влияя на амплитудную характеристику систему, вносит только дополнительный отрицательный фазовый сдвиг.

Рис. 19

Подобное запаздывание свойственно системам, в которых имеет место перемещение материалов, когда между точкой, где произошло како-то изменение переменной, и точкой, где проявляется соответствующий эффект, проходит определенное (конечное) время.

В качестве примера приведем систему управления прокатом стальной полосы, изображенную на рис. 20. Электродвигатель управляет скоростью валков таким образом, чтобы минимизировать ошибку в толщине полосы. Если скорость движения полосы равна v, то запаздывание между точкой изменения скорости валков и точкой измерения толщины полосы равно

.

Рис.20

Таким образом, для уменьшения запаздывания необходимо уменьшать расстояние от валков до точки измерения толщины полосы. Но, так или иначе, влияние запаздывания полностью исключить невозможно, поэтому передаточную функцию разомкнутой системы управления надо рассматривать в виде

W(p)=W1(p)e ^{– pτ}

При этом АФХ системы с запаздыванием приобретает вид

W(jw)=W1(jw)e ^{- jwτ} .

Обычно мы исследуем устойчивость замкнутой системы, построив годограф W(jw) на комплексной плоскости и исследуя его положение относительно точки -1. Аналогично, мы можем построить логарифмические частотные характеристики и исследовать их вид в окрестности точки с координатами 0 дБ и -180^о. Множитель e^-jwτ приводит к дополнительному фазовому сдвигу

φ(w)=-wτ, (*)

который должен быть добавлен к фазовому сдвигу, создаваемому функцией W1(jw). (Обратите внимание, что выражение (*) определяет угол в радианах.) Следующий пример иллюстрирует, как просто учесть запаздывание при анализе устойчивости с помощью построения АФХ W(jw) (Рис.21)

Рис. 21

Для разомкнутой системы с запаздыванием, описываемой передаточной функцией W1(p)e^-pτ можно построить АФХ. Разомкнутая система имеет АФХ W(jw)=W1(jw)e^-jwτ и, следовательно,

|W1(jw)e^-jwτ | =|W1(jw)| и arg W1(jw)e^-jwτ =arg W1(jw) - wτ.

Как видим, АФХ системы с запаздыванием будет отличаться от АФХ системы без запаздывания (разумеется, речь идет о разомкнутых системах) лишь тем, что к arg W1(jw) должен быть добавлен угол –wτ. Этот угол измеряется в радианах и увеличивается с ростом частоты. Результирующая АФХ W(jw) изображена на рис. 22 вместе с годографом для W1(p), который показан пунктирной линией. Мы видим, что единственный эффект запаздывания состоит в том, что он добавляет в систему отставание по фазе. Разумеется, это ухудшает устойчивость системы, поскольку АФХ поворачивается в сторону точки -1.

В ряде случаев необходимо определить максимально допустимую величину запаздывания τ_кр, при которой замкнутая система еще остается устойчивой. Для этого достаточно найти максимальный угол, на который можно повернуть АФХ W1(jw) и чтобы при этом она не охватила точку -1. Этот угол (Рис. 23), очевидно, соответствует запасу устойчивости по фазе системы без запаздывания. Отсюда

.

Следовательно,

- замкнутая система устойчива,

- замкнутая система неустойчива.

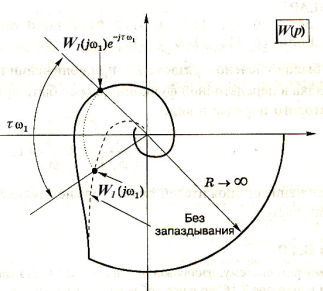
Рис.22

Рис. 23

Критерий устойчивости: если разомкнутая система с запаздыванием не охватывает точку (-1, j0), то замкнутая система с запаздыванием является устойчивой.