
- •Цели и принципы управления
- •1. Понятие об управлении.
- •2. Задачи слежения и регулирования, возмущения и ограничения. Слежение.
- •3. Основные принципы управления.
- •Раздел 2.
- •Типовые (линейные) динамические звенья и их характеристики.
- •1. Усилительное (безинерционное) звено
- •2. Дифференцирующее звено.
- •3. Интегрирующее звено.
- •4. Апериодическое звено.
- •6. Звено второго порядка.
- •Форсирующее звено 2-го порядка
- •Минимально-фазовые звенья
- •3. Описание сау
- •3. Частотные характеристики линейных систем
- •1) Частотные характеристики разомкнутой системы
- •4. Устойчивость систем автоматического управления
- •Геометрическая интерпретация условий устойчивости.
- •6. Робастная устойчивость
- •5. Анализ качества систем автоматического управления
- •1. Понятие о качестве системы
- •2. Точность работы сау в установившемся режиме.
- •Синтез линейных сау
- •1. Понятие о синтезе
- •2. Требования к проектируемой системе.
- •Синтез линейных сау по методу лчх
- •Параметрический синтез сау по методу лчх
- •Коррекция системы с помощью опережения по фазе (реальный пд-регулятор)
- •4. Определим частоту среза скорректированной системы wc*, исходя из .
6. Звено второго порядка.
Дифференциальное уравнение звена второго порядка
![]() (39)
(39)
принято записывать в стандартном виде
![]() , (40)
, (40)
где
![]() - постоянная времени звена;
- постоянная времени звена;
![]() - коэффициент демпфирования, который
определяет склонность переходных
процессов к колебаниям,
- коэффициент демпфирования, который
определяет склонность переходных
процессов к колебаниям,
![]() ; k=b/
; k=b/
![]() - коэффициент усиления.
- коэффициент усиления.
Передаточную функцию звена получим на основе символической записи дифференциального уравнения
![]()
в виде
![]() (41)
(41)
Для определения модальных характеристик запишем характеристическое уравнение звена
![]() =0 (42)
=0 (42)
Оно имеет два корня (полюса), которые в зависимости от коэффициента демпфирования могут быть вещественными или комплексно-сопряженными, что приводит к различным переходным процессам. Рассмотрим варианты корней.
1. Если
≥1,
то корни уравнения (42) вещественные и
положительные. Обозначим их через
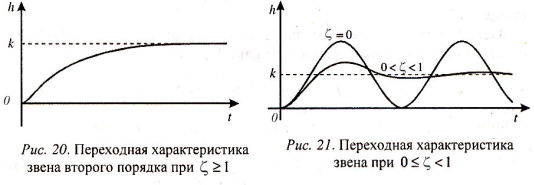
![]() и получим переходную функцию (рис. 20) в
виде
и получим переходную функцию (рис. 20) в
виде
![]() (43)
(43)
2. Если 0≤
<1,
то корни уравнения (42) будут
комплексно-сопряженными, т.е.
![]() .
При
=0
получаем
.
При
=0
получаем
![]()
В случае, когда коэффициент демпфирования изменяется в диапазоне 0< <1, звено второго порядка называют колебательным. Выражение для его переходной характеристики следующее:
![]() (44)
(44)
Причем колебательность переходного процесса будет тем больше, чем меньше коэффициент демпфирования . В пределе при =0 будут иметь место незатухающие колебания. В этом случае звено называется консервативным. Соответствующие графики переходных процессов представлены на рис. 21.
Определим выражение для общей частотной характеристики колебательного звена, заменив р на jw в передаточной функции (41):
![]() (45)
(45)
Запишем выражение для вещественной частотной характеристики
![]() (46)
(46)
и мнимой частотной характеристики:
![]() (47)
(47)
На основе (46) и (47) построим АФХ на комплексной плоскости, рассматривая характерные точки: w=0, w=1/T,…,w→∞. Ее вид существенно зависит от коэффициента демпфирования (рис. 22).
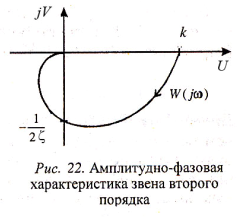
Амплитудно-фазовая характеристика консервативного звена ( =0) начинается в точке k на вещественной оси и при увеличении w стремится к +∞, а затем из -∞ - к началу координат.
Амплитудная частотная характеристика строится на основе выражения
![]() (48)
(48)
и может иметь резонансный пик, высота которого будет тем больше, чем меньше коэффициент демпфирования.
Формула для фазовой частотной характеристики имеет вид
![]() (49)
(49)
Построение ЛАЧХ колебательного звена (при 0< <1) осуществляется по соотношению, полученному из (48):
![]() (50)
(50)
При значениях коэффициента демпфирования в интервале 0,3≤ ≤1 можно строить упрощенную асимптотическую ЛАЧХ, рассматривая отдельно области высоких и низких частот.
В области низких частот (w<<1/T) асимптота имеет вид L1(w)=20lgk.
В области высоких частот, когда w>>1/T, получим вторую асимптоту (рис. 23) L2(w)=20lgk-40lg(Tw).
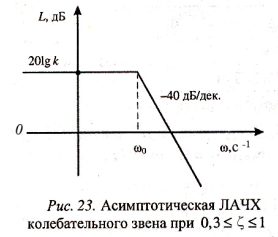
На сопрягающей частоте колебательного звена w0=1/T справедливо соотношение L1(w0)=L2(w0).
Наибольшее отличие асимптотической ЛАЧХ от действительной характеристики наблюдается на частоте w0 (рис. 24) и зависит от величины коэффициента демпфирования.
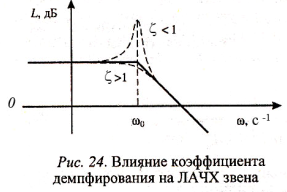
При значениях <0,3 не следует пользоваться асимптотической ЛАЧХ, а нужно строить точную ЛАЧХ.
При >1 корни характеристического уравнения (42) будут вещественными и передаточную функцию звена второго порядка (41) можно представить в виде произведения двух передаточных функций апериодических звеньев:
![]() (51)
(51)
где
![]() - постоянные времени апериодических
звеньев. В этом случае асимптотическая
ЛАЧХ звена второго порядка имеет два
«излома» на частотах w1=1/T1,w2=1/T2.
- постоянные времени апериодических
звеньев. В этом случае асимптотическая
ЛАЧХ звена второго порядка имеет два
«излома» на частотах w1=1/T1,w2=1/T2.
Она может быть получена суммированием асимптотических ЛАЧХ двух апериодических звеньев.
