3. Интегрирующее звено.

Интегрирующим называется звено, поведение которого описывает уравнение

(10)

Примером интегрирующего звена является операционный усилитель в режиме интегрирования.

Основной динамической характеристикой звена является его дифференциальное уравнение

, (11)

на основе которого можно получить передаточную функцию

. (12)

Характеристическое уравнение

D(р)=р=0

имеет единственный корень (полюс), р=0, который представляет собой модальную характеристику интегрирующего звена.

Переходная характеристика звена имеет вид линейно возрастающей функции

, (13)

а весовая функция – ступенчатой функции

. (14)

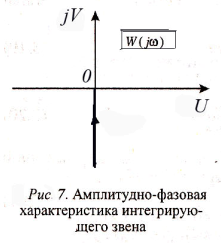
Выражение для амплитудно-фазовой характеристики (рис. 7) получим, заменив в (12) р на jw:

.

Вещественная частотная характеристика отсутствует, U(w)=0. Мнимая частотная характеристика имеет вид

V(w)=-k/w,

а амплитудная частотная характеристика

R(w)=k/w.

При этом фазовая частотная характеристика следующая:

, (15)

т.е. звено имеет постоянный фазовый сдвиг, который не зависит от частоты.

Амплитудно-фазовая характеристика интегрирующего звена имеет вид прямой, совпадающей с отрицательной мнимой полуосью комплексной плоскости (рис. 7).

Запишем выражение для логарифмической амплитудно-частотной характеристики

L(w)=20lgk/w=20lgk - 20lgw (16)

и изобразим ее график (рис. 8).

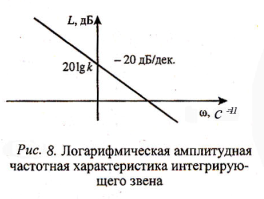
Как видим, логарифмическая амплитудно-частотная характеристика интегратора представляет собой прямую с наклоном -20 дБ/дек, и пересекает ось ординат в точке 20lgk. Она показывает, что звено усиливает низкочастотные сигналы и ослабляет высокочастотные.

4. Апериодическое звено.

Апериодическим называется звено, дифференциальное уравнение которого имеет вид

. (17)

Различного типа двигатели являются примерами такого звена.

Дифференциальное уравнение апериодического звена принято записывать в стандартном виде:

, (18)

где - постоянная времени; - коэффициент усиления звена.

Заменив в (18) d/dt на D, перейдем к символической записи дифференциального уравнения

(TD+1)y=kv (19)

и найдем передаточную функцию апериодического звена:

. (20)

Для определения модальных характеристик по передаточной функции (20) запишем характеристическое уравнение

D(р)=Тр+1=0. (21)

Оно имеет единственный корень (полюс), р=-1/Т.

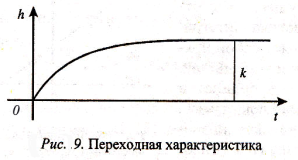
Переходную характеристику звена (рис. 9) можно найти как решение уравнения (18) при v=1(t) и y(0)=0:

(22)

Весовую функцию (рис. 10) вычислим по соотношению

(23)

Выражение, соответствующее амплитудно-фазовой характеристике апериодического звена, имеет вид

(24)

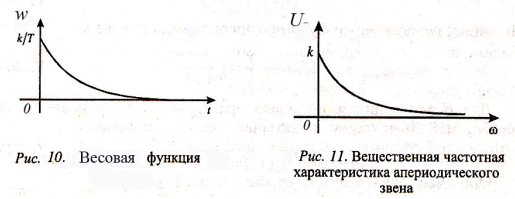
По выражению

(25)

можно построить его вещественную частотную характеристику (рис. 11).

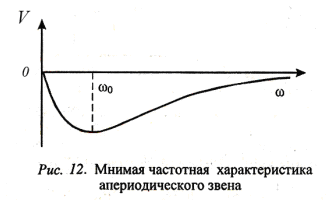
Мнимая частотная характеристика (рис. 12) апериодического звена соответствует уравнению

(26)

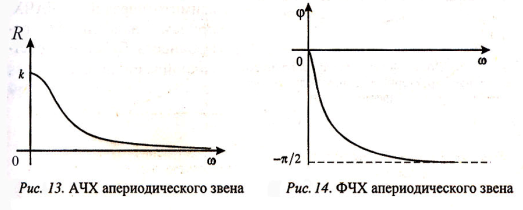
Амплитудную частотную характеристику (рис. 13) описывает выражение

(27)

Фазовая частотная характеристика звена определяется соотношением

(28)

Она представляет собой кривую (рис. 14) с пределом .

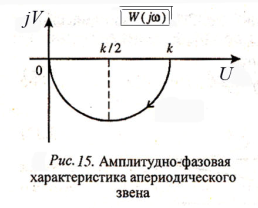
На комплексной плоскости по выражению (24) можно построить амплитудно-фазовую характеристику апериодического звена, которая имеет вид полуокружности (рис. 15).

Запишем выражение для логарифмической амплитудно-частотной характеристики

(29)

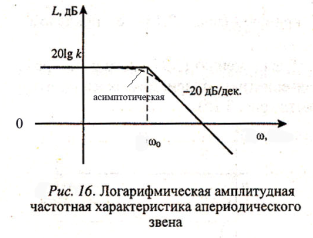
Наиболее просто для звена можно построить асимптотическую логарифмическую амплитудно-частотную характеристику. В этом случае следует рассмотреть отдельно области высоких и низких частот и для каждой определить свою асимптоту:

1) в области низких частот, когда w<<1/T, вместо точной ЛАЧХ (29) можно рассмотреть приближенную

L1(w)=20lgk; (30)

2) в области высоких частот при w>>1/T вторая асимптота имеет вид

L2(w)=20lgk-20lg(Tw) (31)

На частоте w0=1/T, которая называется сопрягающей частотой апериодического звена, справедливо условие

L1(w0)=L2(w0)

Точная характеристика звена на рис. 16 показана пунктирной линией и несколько отличается от асимптотической ЛАЧХ, причем наибольшая погрешность будет на сопрягающей частоте w0.

5. Форсирующее звено.

Форсирующим называется звено, дифференциальное уравнение которого имеет вид:

. (32)

Нетрудно убедиться в том, что (32) можно представить как сумму уравнений пропорционального и дифференцирующего звеньев.

Передаточную функцию форсирующего звена

принято записывать в стандартной форме

W(p)=k(1+Tp), (33)

где k=k1 – коэффициент усиления, а T=k2/k1 – постоянная времени звена.

Передаточная функция (33) содержит полином в числителе, корень которого z=-1/T называется «нулем» форсирующего звена.

Его переходная характеристика определяется соотношением

. (34)

Качественный вид ее приведен на рис. 17.

Весовая функция звена следующая:

(35)

Амплитудно-фазовая характеристика находится по передаточной функции (33) и имеет вид

W(jw)=k(1+jTw). (36)

Соответствующая амплитудно-фазовая характеристика изображена на рис. 18.

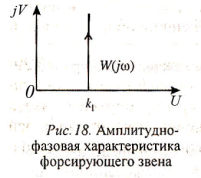
Вещественная частотная характеристика звена не зависит от частоты и равна U(w)=k, мнимая частотная характеристика представляет собой прямую V(w)=kTw.

Амплитудная частотная характеристика может быть построена по выражению

,

а фазовая частотная характеристика определяется в виде

(3.37)

причем в пределе .

На основании выражения для R(w) определим логарифмическую амплитудную частотную характеристику

(3.38)

Как и в предыдущем случае, для форсирующего звена удобнее строить не точную, а асимптотическую ЛАЧХ (рис. 19). Здесь w0=1/T – сопрягающая частота звена.

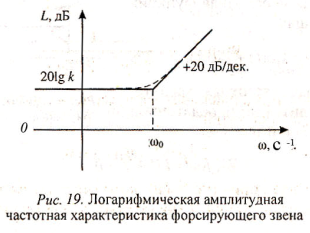
Причем ее можно получить, исследуя отдельно области низких и высоких частот или суммируя ЛАЧХ пропорционального и дифференцирующего звеньев.

Нетрудно убедиться, сравнивая выражения (28) и (29) с выражениями (37) и (38), в том, что логарифмические амплитудная и фазовая частотные характеристики форсирующего звена представляют собой зеркальное отображение относительно оси абсцисс соответствующих логарифмических характеристик апериодического звена.