2. Точность работы сау в установившемся режиме.

В общем случае на САУ оказывают влияние задающее воздействие v(t), возмущающее воздействие f(t) и шум измерения s(t). При этом изображение по Лапласу у(р) выходной величины y(t) линейной системы может быть записано в виде

y(p)=Ф(p)v(p)+Ф_f(p)f(p)+Ф_s(p)s(p), (1)

где Ф(р) – передаточная функция замкнутой системы;

Ф_f(p) – передаточная функция по возмущению f(p)=L{f(t)};

Ф_s(p) – передаточная функция по шуму измерения s(p)=L{s(t)};

v(p)=L{v(t)} - изображение по Лапласу задающего воздействия v(t).

Задачей САУ является обеспечение в любой момент времени равенства величин: y(t)=v(t). Однако реальная система выполняет эту задачу с некоторой ошибкой

ε_п(t)=v(t)-y(t) (2)

равной разности между заданным v(t) и действительным y(t) значениями управляемой величины. Изображение по Лапласу этой ошибки с учетом (1) равно

ε_п(р)=v(p)-y(p)= ε(p)+ ε_f(p)+ ε_s(p) (3)

где

ε(p)=[1-Ф(p)]v(p); (4)

ε_f(p)=-Ф_f(p)f(p); (5)

ε_s(p)=-Ф_s(p)s(p). (5,а)

Таким образом, ошибка системы состоит из трех составляющих

ε_п(t)= ε(t)+ ε_f(t)+ ε_s(t) (6)

первая из которых ε(t)=L^-1[ε(p)] называется ошибкой воспроизведения, вторая ε_f(t)=L^-1[ε_f(p)] - ошибкой по возмущению, а третья ε_s(t)=L^-1[ε_s(p)] – ошибкой по шуму измерения.

Ошибка воспроизведения показывает, как точно воспроизводит данная система задающее воздействие v(t) в отсутствие других внешних воздействий (f=s=0). Величина этой ошибки определяется инерционностью системы и видом задающего воздействия v(t).

Ошибки по возмущению и шуму измерения соответственно показывают, как влияют на управляемую величину возмущение и шум измерения при задающем воздействии v(t), равном нулю. Такое разделение ошибки на три составляющие возможно лишь в линейных системах, для которых справедлив принцип суперпозиции.

Выражение (6) для устойчивых систем определяет ошибку как в установившемся, так и в переходном режимах. Переходная составляющая ошибки обычно рассматривается при исследовании переходных процессов. Поэтому в данной главе остановимся на рассмотрении ошибки в установившемся режиме, который теоретически наступает при t→∞. Величина установившейся ошибки

(ε_п)_уст(t)= ε_уст(t)+ (ε_f)_уст(t)+ (ε_s)_уст(t) (7)

характеризует точность работы САР в установившемся режиме.

Рассмотрим методы вычисления установившейся ошибки воспроизведения ε_уст(t) и установившейся ошибки по возмущению (ε_f)_уст(t).

Ошибка воспроизведения.

Установившееся значение ошибки воспроизведения в ряде случаев определяется с помощью известной в операционном исчислении теоремы о конечном значении, которая применительно к данному случаю может быть записана в виде

ε_уст= (8)

Преобразование Лапласа ε(р) ошибки легко найти, если известны преобразование Лапласа v(р) входного сигнала и передаточная функция для ошибки Ф_ε(р), связанная с передаточной функцией Ф(р) замкнутой системы соотношением

Ф_ε(р)=1-Ф(р) (9)

Действительно, согласно (4)

ε(р)=Ф_ε(р)v(p) (10)

Принимая во внимание существующую связь между передаточными функциями замкнутой Ф(р) и разомкнутой W(р) систем

Ф(р)=W(p)/(1+W(p)),

а также, что

_,

на основании (9) имеем

Ф_ε(р)=

Передаточная функция по ошибке называется также функцией чувствительности.

Следовательно,

(11)

Учитывая, что W₀(p) обладает свойством W₀(0)=1 получаем

(12)

Выражение (12) имеет смысл, если ε(t) стремится к определенному пределу при t→∞. В противном случае выражение (8) неприменимо. Рассмотрим от каких факторов зависит ошибка ε_уст при типовых входных сигналах, для которых вышеуказанное требование соблюдается.

Входной сигнал – ступенчатая функция v(t)=a₀1(t).

Операторное выражение такой функции v(p)=a₀/p. При этом

(13)

Если ν=0 (система не содержит интегрирующих звеньев), то

(14)

Следовательно, в такой системе, даже при постоянном входном сигнале, имеет место ошибка, называемая ошибкой по положению или статической ошибкой. Ошибка при известном а₀ определяется статизмом системы

(15)

и она тем меньше, чем больше коэффициент усиления k.

Системы, обладающие статической ошибкой, называются статическими системами. Коэффициент усиления k статических систем является безразмерной величиной, так как величины а₀ и ε_уст имеют одинаковую размерность.

Отметим, что статическая ошибка, определяемая выражением (14), является принципиальной (методической) ошибкой и обусловлена принципом действия системы.

Если ν>1 (система содержит одно или несколько интегрирующих звеньев), то, как это видно из выражения (13), статическая ошибка равна нулю. Системы, обладающие нулевой статической ошибкой, называются астатическими системами. При этом величина ν, как говорят, определяет порядок астатизма системы.

Астатическую систему можно рассматривать как статическую систему с бесконечно большим коэффициентом усиления k. Действительно, наличие интегрирующих звеньев приводит к тому, что при постоянном входе сигнал на выходе разомкнутой системы с течением времени растет до бесконечности.

Входной сигнал v(t)=a₁t, изменяющийся с постоянной скоростью a₁.

В этом случае v(p)=a₁/p², а установившаяся ошибка

(16)

Если ν=0 (статическая система), то ε_уст=∞. Полученному результату легко дать объяснение, если учесть, что в установившемся режиме, т.е. при t→∞, на входе системы имеется бесконечно большой сигнал и поэтому при конечном коэффициенте усиления k, согласно (14), ошибка ε_уст равна бесконечности. Другими словами, данный случай можно рассматривать как предыдущий при v(t)=a₀, если положить a₀=∞.

Если ν=1 (система с астатизмом первого порядка), то

(17)

При этом ошибка ε_уст обратно пропорциональна коэффициенту усиления и носит название скоростной ошибки. Так как входной сигнал v и ошибка ε имеют одинаковую размерность, то коэффициент усиления системы с астатизмом первого порядка имеет размерность [сек^-1] и характеризует установившуюся скорость изменения выходной величины разомкнутой системы при постоянном входном сигнале.

Физический смысл полученного результата виден на примере простейшей следящей системы (рис. 1). Если на входе имеем сигнал v, изменяющийся с постоянной линейной скоростью a₁, то установившийся режим будет иметь место лишь в случае, когда выходная величина у будет изменяться с той же скоростью а₁.

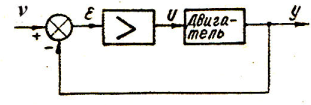
Рис. 1

Но для этого необходимо подвести к двигателю определенное напряжение U=a₁/K_дв, зависящее от коэффициента усиления двигателя К_дв. Это напряжение может появиться только при наличии сигнала ошибки ε_уст. Чем больше коэффициент усиления усилителя К_ус, а следовательно, и всей системы – К=К_усК_дв, тем меньшее значение ε_уст=а₁/К_ус требуется для вращения двигателя со скоростью, равной скорости изменения входного сигнала.

Используя выражение (17), по заданным значениям скорости а₁₀ и скоростной ошибки (ε_ск)_доп можно найти величину коэффициента усиления

(18)

обеспечивающую требуемую точность воспроизведения сигнала v(t)=a₁₀t.

Если ν≥2 (система с порядком астатизма выше первого), то скоростная ошибка равна нулю.

Входной сигнал , изменяющийся с постоянным ускорением а₂.

Так как , то ошибка с учетом (12)

(19)

Если ν=0, 1, то установившаяся ошибка равна бесконечности. Если ν=2 (система с астатизмом второго порядка), то ошибка определяется выражением

(20)

и носит название ошибки по ускорению. Как видно их этого выражения, коэффициент усиления системы с астатизмом второго порядка имеет размерность [сек^-2].

Если ν≥3, то установившаяся ошибка равна нулю.

Таким образом, точность работы САУ при входных сигналах вида степенной функции

(20а)

зависит только от порядка астатизма ν и коэффициента усиления k системы, причем, чем больше значения ν и k, тем меньше величина ошибки воспроизведения.

Формулу (12) для определения ошибки ε_уст удобно использовать, если входное воздействие представляет собой степенную функцию вида (20а). Однако на практике часто встречаются входные сигналы, которые меняются достаточно медленно по известному, а порой и неизвестному, законам. Обычно такие сигналы на некотором текущем интервале времени можно представить в виде ряда Тейлора. В этом случае удобно ввести понятие о коэффициентах ошибок, с помощью которых нетрудно найти установившуюся ошибку воспроизведения.

Понятие о коэффициентах ошибок

Пусть входной сигнал v(t) меняется настолько медленно, что на текущем интервале времени, соизмеримом с длительностью переходного процесса в системе (речь идет о практической длительности переходного процесса t_р), он может быть с достаточной степенью точности представлен в виде полинома степени r

(21)

где a_i=v⁽ⁱ⁾(t) – i-ая производная сигнала v(t).

Если известна весовая функция замкнутой системы k(t), то значение выходного сигнала определяется интегралом свертки

Если момент приложения входного сигнала достаточно удален от текущего момента времени, т.е. t₀=-∞, то в системе к интересующему нас моменту t≥0 переходный процесс уже наверняка закончится, так что будет иметь место установившийся процесс, который определяется выражением

,

отсюда

(22)

Вводя обозначение

(23)

получаем другое выражение для выходной величины

(24)

Величины , определяемые согласно (23), называются моментами весовой функции.

При этом установившаяся ошибка

(25)

Обозначая

(26)

получаем

(27)

Входящие в выражение (27) коэффициенты C_i получили название коэффициентов ошибок.

Если известны значения производных входного сигнала, то по формуле (27) легко вычислить установившуюся ошибку. При этом система будет тем точнее, чем меньше величины коэффициентов ошибок. Следовательно, коэффициенты ошибок можно рассматривать как показатели качества системы при медленно меняющихся воздействиях.

Дл я определения коэффициентов ошибок удобно выражать моменты весовой функции ; i=0,1,2,… непосредственно через передаточную функцию системы Ф(р). По определению

Дифференцируя это выражение i раз по р, получим

Положив в этом выражении р=0, получим

(28)

Сравнивая выражения (28) и (23), находим

(29)

или =Ф₀(0), , , …

Вычисление величин непосредственно по формуле (29) связано с громоздкими выкладками. Эти выкладки значительно упрощаются, если представить передаточную функцию Ф(р) в виде отношения двух многочленов

Ф(р)=К(р)/Д(р) или Ф(р)Д(р)=К(р) (30)

где

Разложим функцию Ф(р) в ряд Маклорена в окрестности точки р=0. Учитывая выражение (29), получим

Выражение (30) при этом принимает вид

Приравнивая коэффициенты при одинаковых степенях р, например при рⁱ в правой и левой частях этого выражения, получим

или

(31)

Полученная формула является рекуррентной и позволяет последовательно вычислять коэффициенты . Для нескольких первых коэффициентов получаются следующие формулы

(32)

Пример. Пусть передаточная функция разомкнутой системы определяется выражением W(p)=k/p(Tp+1), а входной сигнал изменяется по закону v(t)=arctgαt.

Передаточная функция замкнутой системы имеет вид

Следовательно,

К(р)=k, Д(р)=k+р+Тр²

Отсюда

m=1, n=2, a₂=k, a₁=1, a₀=T, b₀=k, b₁=0.

В соответствии с формулами (32) определяем моменты весовой функции

, , …

Учитывая выражение (26), находим коэффициенты ошибок

Так как , то, ограничившись учетом первых двух слагаемых ошибки, получаем

Графики изменения входного сигнала и ошибки приведены на рис.2. При t=0 ошибка достигает максимального значения, равного α/k.

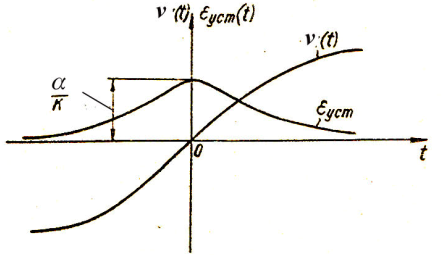
Рис. 2.

Заметим, что коэффициенты ошибок представляют собой коэффициенты разложения передаточной функции по ошибке Ф_ε(р) в ряд Маклорена в окрестности точки р=0. Действительно, передаточная функция по ошибке связана с передаточной функцией замкнутой системы

соотношением

Ф_ε(р)=1-Ф(р)

Учитывая, что коэффициенты ошибок определяются через моменты весовой функции согласно (26) как

получаем

(33)

что и требовалось показать. Следовательно, коэффициенты ошибок можно найти по формуле

(34)

Коэффициенты ошибок статических и астатических систем.

Первые три коэффициента ошибок С₀, С₁, С₂ имеют специальные названия, соответствующие их физическому смыслу.

Коэффициент С₀ называется коэффициентом статической ошибки ε_ст или коэффициентом ошибки по положению, так как он определяет величину установившейся ошибки при постоянном входном сигнале. Действительно, если v(t)=a₀=const, то согласно (27) ε_уст= ε_ст=С₀а₀. Последняя формула позволяет дать другое определение для статических и астатических систем.

Системы, для которых ε_ст≠0, по введенному выше определению, называются статическими системами. Однако ε_ст≠0 только тогда, когда С₀≠0. Следовательно, неравенство нулю коэффициента ошибки С₀ является признаком статической системы.

В астатических системах статическая ошибка равна нулю. Поэтому условие С₀=0 обеспечивает системе автоматического управления астатизм первого порядка.

Коэффициент С₁ называется коэффициентом ошибки по скорости, так как от него зависит величина ошибки по скорости ε_ск. Если С₀=0, а С₁≠0, то система имеет постоянную ошибку по скорости при входном сигнале, меняющемся с постоянной скоростью. Действительно, когда v(t)=a₁t, то v’(t)=a₁, v’’(t)=0 и ε_уст= ε_ск=С₁а₁. Если С₀=С₁=0, то ε_ск=0, т.е система имеет астатизм второго порядка. Такая система, как известно, отрабатывает входной сигнал, меняющийся с постоянной скоростью, без ошибки.

Наконец, величина С₂ называется коэффициентом ошибки по ускорению, так как от нее зависит величина ошибки по ускорению. Если С₀=С₁=0, а С₂≠0, то система отрабатывает с постоянной ошибкой сигнал, меняющийся с постоянным ускорением а₂. Действительно, когда v(t)= a₂t², то v’(t)=a₂t, v’’(t)=a₂, v’’’(t)=0, так что ε_уст= ε_уск=С₂а₂=const.

Если С₀=С₁=С₂=0, то ε_уск=0, т.е. система имеет астатизм третьего порядка. Такая система отрабатывает без ошибки входной сигнал, меняющийся с постоянным ускорением.

Как видим, число первых нулевых коэффициентов ошибок определяет порядок астатизма системы.

Полученный результат легко обобщить на замкнутую систему с единичной обратной связью и с порядком астатизма, равным ν, которая в разомкнутом состоянии имеет передаточную функцию

Действительно, передаточная функция по ошибке

(35)

где

Следовательно, коэффициент статической ошибки согласно (34)

(36)

Полагая ν≥1, разложим в ряд Маклорена в окрестности точки р=0:

Так как , то согласно (35)

Ранее показали (см. (33)), что

Приравнивая коэффициенты при одинаковых степенях р у двух последних выражений, получаем

Следовательно, для системы с единичной обратной связью, содержащей ν интегрирующих звеньев, первые ν коэффициентов ошибок обращаются в нуль, т.е. такая система имеет ν-ый порядок астатизма.

Следует отметить, что определение астатической системы порядка ν как системы, у которой первые ν коэффициентов ошибок равны нулю, является более общим, чем ее определение как системы, имеющей ν интегрирующих звеньев. Ниже будут даны методы, позволяющие повышать порядок астатизма, не используя интегрирующие звенья.

Ненулевые коэффициенты ошибок С_i обязательно включают в себя в качестве делителя коэффициент усиления системы. Поэтому с увеличением коэффициента усиления величина ненулевых коэффициентов ошибок уменьшается.

В заключение нужно отметить, что для системы с единичной обратной связью основное значение в вопросе обеспечения заданной точности имеют коэффициент усиления и порядок астатизма. Однако, стремление увеличить коэффициент усиления и (или) порядок астатизма может повлечь за собой дестабилизацию системы.

Ошибка по возмущению

Методика определения установившейся ошибки по возмущению ε_fуст принципиально не отличается от рассмотренных способов определения установившейся ошибки воспроизведения. При типовых возмущающих сигналах вида степенных функций используют теорему о конечном значении, согласно которой

ε_fуст= (38)

В случае воздействия на систему одного возмущения f(t) с учетом (5) получим

ε_fуст=- (39)

Если же возмущение f(t) – медленно меняющийся сигнал, представляемый конечным числом слагаемых ряда Тейлора

(40)

то установившаяся ошибка по возмущению подсчитывается по формуле

ε_fуст(t)= (41)

где коэффициенты C’₀,C’₁,C’₂,… представляют собой коэффициенты ошибок по возмущению, определяемые по формуле

(42)

Коэффициенты ошибок по возмущению С’_I в общем случае отличаются от коэффициентов ошибок воспроизведения С_i. Поэтому требует уточнения ранее сформулированное определение статических и астатических систем. Все, что говорилось ранее по данному вопросу, справедливо для систем, астатических по отношению к входному сигналу. Так, если С₀=0, то система имеет астатизм первого порядка по отношению к входу; если С₀=С₁=0, то система обладает астатизмом второго порядка относительно входного сигнала.

Теперь введем понятие астатизма системы по отношению к возмущению. Системы, для которых С’₀=0, называются астатическими по отношению к возмущению с астатизмом первого порядка. Такие системы полностью устраняют влияние на регулируемую величину в установившемся состоянии постоянных возмущений f(t)=f₀=const.

Наконец, системой ν_f-го порядка астатизма по отношению к возмущению называется система, для которой

C’₀=C’₁=…=C’_νf-1=0 (43)

Рассмотрим вопрос о том, каким образом можно обеспечить астатизм системы по возмущению. С этой целью исследуем систему, структура которой представлена на рис. 3. Пусть передаточная функция объекта W₁(p) включает ν₁ интегрирующих звеньев, а передаточная функция управляющего устройства W₂(p) – ν₂ интегрирующих звеньев, так что

, (43а)

причем W10(0)=W20(0)=1.

Рис. 3.

Докажем, что порядок астатизма системы по возмущению определяется числом интегрирующих звеньев ν₂, содержащихся в звене УУ, расположенном между входом системы и точкой приложения возмущения, т.е. докажем, что при ошибка ε_fуст=0, если ν₂>i.

Передаточная функция по возмущению

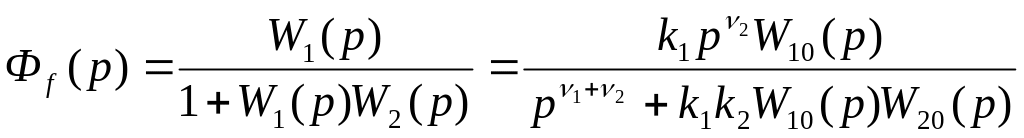(44)

Подставляя полученное выражение в формулу (39), находим

ε_fуст = (45)

Учитывая, что , получим

ε_fуст =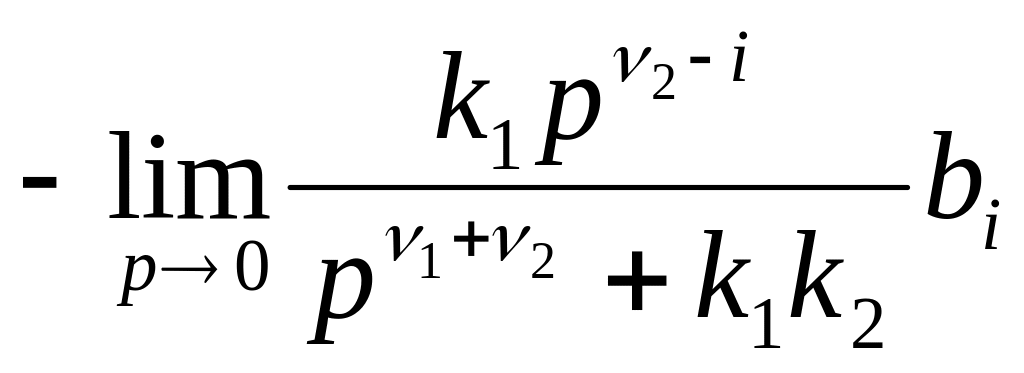 (46)

Отсюда

ε_fуст = (47)

независимо от величины ν₁.

Следовательно, ν₂ первых коэффициентов ошибок по возмущению равны нулю, т.е.

С’_i=0, i=0,1,…, ν₂-1

и система имеет порядок астатизма ν_f= ν₂ по отношению к возмущению f(t).

Если элемент с передаточной функцией W₂(p)не содержит интегрирующих звеньев, то наличие последних в элементе с передаточной функцией W₁(p) не может придать системе астатизм по возмущению. Заметим, что порядок астатизма системы по отношению к входному сигналу определяется общим числом интегрирующих звеньев, т.е. величиной ν=ν₁+ν₂.

Если ν₂=I, то ошибка по возмущению – постоянная величина, определяемая выражением

ε_fуст = (48)

В этом случае ошибка ε_fуст может быть уменьшена путем увеличения коэффициента усиления k₂, что приводит к увеличению коэффициента усиления всей системы k=k₁k₂.

Понятие об инвариантных системах

В предыдущем параграфе этой главы рассматривался вопрос о вычислении установившейся ошибки системы при известном законе изменения внешних воздействий. Зная, от каких факторов зависит ошибка, можно заметить пути обеспечения заданной точности системы.

Однако в целом ряде случаев законы изменения сигналов v(t) и f(t) оказываются неизвестными и фактически мы даже не располагаем никакой априорной информацией об этих воздействиях, в том числе и статического характера, кроме информации о том, что эти сигналы существуют и приложены к определенным точкам структурной схемы.

При этом возникает задача создания системы, которая была бы нечувствительна к возмущениям произвольного вида и воспроизводила без искажения входной сигнал произвольного вида. Теория инвариантности как раз и рассматривает методы решения поставленной задачи.

Основным понятием теории инвариантности является понятие абсолютно инвариантной системы. Системой, абсолютно инвариантной к задающему воздействию v(t), называется система, имеющая нулевую установившуюся ошибку воспроизведения ε_уст(t) при любом законе изменения v(t). Системой, абсолютно инвариантной к возмущению f(t), называется система, имеющая нулевую установившуюся ошибку по возмущению ε_fyст(t) при любом законе изменения f(t). Учитывая существующие выражения для изображений этих ошибок

ε(р)=Ф_ε(р)v(p) и ε_f(p)=-Ф_f(p)f(p);

нетрудно установить, что условия абсолютной инвариантности сводятся к требованию равенства нулю передаточных функций по ошибке Ф_ε(р) и по возмущению Ф_f(p), т.е.

Ф_ε(р)=0, Ф_f(p)=0 (49)

Рассмотрим условия физической осуществимости абсолютно инвариантных систем. Вопрос об этих условиях, возникающий при проектировании инвариантных систем, весьма важен.

Необходимое условие физической осуществимости заключается в выполнении системой условий инвариантности (49) как в замкнутом, так и в разомкнутом состоянии, другими словами, абсолютно инвариантная система не должна терять своих свойств при отключении обратной связи. Для обеспечения необходимого условия в системы вводятся дополнительные связи по возмущению и по входному сигналу. При этом возникает потребность в удовлетворении достаточного условия.

Достаточным условием физической осуществимости абсолютно инвариантных систем является физическая реализуемость дополнительно вводимых в систему элементов. Порядок знаменателя передаточной функции физически реализуемых элементов превышает (в крайнем случае равен) порядок числителя этой же функции.

Обычно построить абсолютно инвариантную систему оказывается затруднительным. Поэтому на практике используют селективные абсолютно инвариантные системы, которые позволяют обеспечить нулевую установившуюся ошибку при некоторых определенных видах внешних воздействий. Условие абсолютной селективной инвариантности к задающему воздействию, изменяющемуся по известному закону v(t), выглядит следующим образом:

v(t):ε_уст(t)=0 (50)

Фактически условие селективной абсолютной инвариантности заключается в требовании равенства нулю нескольких первых коэффициентов ошибок системы или, другими словами, в требовании определенного порядка астатизма системы, как это имеет место, если v(t) является степенной функцией или полиномом.

Поэтому коэффициенты ошибок называют также коэффициентами инвариантности системы.

В системах, использующих принцип управления по ошибке, порядок астатизма может быть увеличен в основном за счет увеличения числа интегрирующих звеньев. Однако обеспечение устойчивости систем с большим числом интегрирующих звеньев представляет собой трудную задачу.

Более удобным способом повышения порядка астатизма является введение дополнительных связей по возмущению и по входному сигналу, т.е. переход к системам, использующим комбинированный принцип управления. Такие дополнительные связи не влияют на устойчивость системы. При их включении характеристическое уравнение замкнутой системы не меняется. Поэтому в подобных системах можно повышать порядок астатизма, не затрагивая условий устойчивости.

Введение связей по возмущению

В случае, когда возмущающее воздействие можно измерить с помощью датчика, то за счет введения связи по возмущению можно добиться даже абсолютной инвариантности системы к возмущающему воздействию, не затрагивая при этом условия устойчивости.

Структурная схема системы с обратной связью и со связью по возмущению, описываемой передаточной функцией W₃(p), представлена на рис. 4. Разумеется, передаточная функция связи по возмущению отражает так же динамические свойства датчика, с помощью которого измеряется возмущающее воздействие.

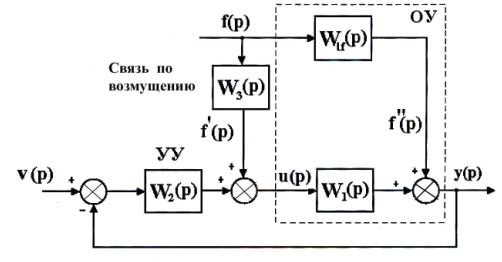
Рис. 4

Здесь W_1f(p) - передаточная функция объекта по возмущению,

W₁(p) – - передаточная функция объекта по управлению.

Передаточную функцию по возмущению Ф_f(р) для системы на рис. 4, можно найти, положив задающее воздействие равным нулю, т.е. положив v(p)=0, и используя принцип суперпозиции, в силу которого реакцию системы можно рассматривать как сумму реакций на каждый из сигналов f’(p)=W₃(p)f(p) и f’’(p)=W_1f(p)f(p), взятых в отдельности. Отсюда

Следовательно,

(51)

В соответствии с условием (49) абсолютная инвариантность к возмущающему воздействию обеспечивается, если Ф_f(p)=0. Приравнивая к нулю выражение (51), находим передаточную функцию связи по возмущению

W₃(p)=-W_1f(p)/W₁(p) (52)

обеспечивающую выполнение условия абсолютной инвариантности системы к возмущающему воздействию.

С физической точки зрения нулевую установившуюся ошибку по возмущению, получаемую при этом для каждого вида возмущающего воздействия, можно объяснить следующим образом. При передаточной функции W₃(p), описываемой выражением (52), возмущающее воздействие, пройдя последовательно через связь по возмущению и часть объекта управления с передаточной функцией W₁(p), компенсирует сигнал f’’(p), приложенный к выходу объекта управления и порожденный непосредственным, а не искусственным влиянием возмущения на объект. Во многих случаях условие (52) можно реализовать, так как знаменатель передаточных функций объекта управления

W_1f(p)=-K_1f(p)/D₁(p), W₁(p)=-K₁(p)/D₁(p)

оказывается одинаковым и равным D₁(p). При этом из (52) получаем передаточную функцию связи по возмущению

W₃(p)=-K_1f(p)/K₁(p) (53)

которая обычно физически осуществима, т.е. степень K₁(p) не ниже степени K_1f(p), так что degK₁≥degK_1f.

Если условие физической осуществимости связи по возмущению, описываемой (52), не выполняется, можно обычно реализовать селективную инвариантность к возмущающему воздействию. В этой связи отметим, что за счет связи по возмущению часто добиваются выполнения условий астатизма системы, т.е. условия абсолютной селективной инвариантности к постоянному возмущающему воздействию. Так как изображение постоянного возмущающего воздействия f(t)=b₀=const равно f(p)=b₀/p, то в соответствии с (42) условие астатизма по отношению к возмущающему воздействию можно записать в этом случае как

C’₀=Ф_f(0)=0.

Полагая в (51) р=0 и приравнивая затем полученное выражение к нулю, находим коэффициент усиления связи по возмущению

k₃=W₃(0)=-W_1f(0)/W₁(0),

гарантирующий астатизм системы по возмущению для любых значений b₀.

Недостатком приведенной на рис. 4 структурной схемы является зависимость передаточной функции W₃(p) от свойств объекта. Вариации параметров передаточной функции объекта управления W₁(p) относительно принятых при расчете передаточной функции W₃(p) приведут к нарушению как абсолютной, так и селективной инвариантности, хотя при соответствующем выборе передаточной функции обратной связи W₂(p) можно в значительной степени ослабить чувствительность системы к изменению параметров объекта управления. Упомянутые вариации параметров обусловлены неточностью, неопределенностью и изменчивостью математической модели объекта управления.

Селективная абсолютная инвариантность к задающему воздействию в системах с единичной обратной связью. Принцип внутренней модели.

Рассмотрим систему с единичной обратной связью, т.е. систему, в которой используется принцип управления по ошибке.

Пусть задающему воздействию v(t) соответствует изображение

v(p)=K_v(p)/D_v(p) (54а)

и известны полюсы этого изображения, другими словами, корни уравнения

D_v(p)=0,

Причем степень полинома D_v(p) равна degD_v. Тогда уравнение селективной абсолютной инвариантности v(t):ε_уст(t)=0

можно записать по отношению к передаточной функции разомкнутой системы в виде

(55)

где D(p)= .

При этом передаточная функция по ошибке оказывается равной

(55б)

где Д(р)=D(p)+К(р) есть характеристический многочлен замкнутой системы управления (знаменатель передаточной функции Ф(р)), и ε_уст=0. Действительно, с учетом ε(p)=Ф_ε(р)v(p), (54а) и (55б) изображение ошибки

содержит лишь полюсы проектируемой системы р_i, i= , т.е. корни уравнения Д(р)=0, degД=n, которые для обеспечения устойчивости должны быть левыми. Следовательно, ошибка воспроизведения при простых корнях

,

с течением времени стремится к нулю, т.е.

.

Вывод. Передаточная функция W₂(p) управляющего устройства, обеспечивающего селективную абсолютную инвариантность системы управления к задающему воздействию, должна включать как свои полюсы все полюсы изображения этого задающего воздействия. Приведенный вывод можно рассматривать как конкретизацию принципа внутренней модели, который говорит о том, что хорошая система должна содержать модель внешней среды, в данном случае передаточная функция разомкнутой системы должна включать в себя математическую модель задающего воздействия, точнее знаменатель D_v(p) в изображения задающего воздействия.

Из этого вывода следует, что условие селективной абсолютной инвариантности можно записать как .

Пример1. Пусть задающее воздействие – постоянный сигнал v(t)=a₀, так что V(p)=a₀/p, q₁=0, и условие селективной абсолютной инвариантности принимает вид: W(0)=∞, т.е. значение АЧХ разомкнутой системы на нулевой частоте должно быть равно бесконечности, другими словами, ПФ разомкнутой системы должна включать в себя хотя бы одно интегрирующее звено – система должна обладать астатическими свойствами.

Пример2. Пусть задающее воздействие – гармонический сигнал v(t)=v₀sinw_vt, с амплитудой v₀ и частотой w_v. Тогда V(p)=v₀w_v/(p²+w²_v), q_1,2=±jw_v. При этом условие селективной абсолютной инвариантности принимает вид: W(jw_v)=∞, т.е. значение АЧХ разомкнутой системы на частоте задающего воздействия | W(jw_v)| должно быть равно бесконечности, другими словами, знаменатель ПФ разомкнутой системы должен содержать сомножитель p²+w²_v.

Заметим, что в селективной абсолютной инвариантной системе с единичной обратной связью нулевая установившаяся ошибка воспроизведения сохраняется независимо от уровня задающего воздействия, а также от параметров объекта управления. Дело в том, что условие инвариантности (55), записанное применительно к передаточной функции разомкнутой системы не зависит от передаточной функции объекта управления. При этом, как говорят, свойство селективной абсолютной инвариантности робастно.

Селективная инвариантность до ε к задающему воздействию.

Под селективной инвариантностью до ε понимается ограниченность установившейся ошибки воспроизведения задающих воздействий v(t) определенного вида. При такой форме инвариантности имеет место условие

(23)

где - некоторая постоянная.

Селективная инвариантность до ε к гармоническому задающему воздействию.

Для задающих воздействий, изображения которых содержат лишь простые полюсы q_k, условие селективной инвариантности до ε можно записать в виде

(36)

Гармоническое задающее воздействие

v(t)=v₀sinw_vt

с изображением

и полюсами q_1,2=±jw_v как раз относится к таким воздействиям, поэтому условие (36) для гармонического задающего воздействия можно записать так:

(37)

При этом мы учитываем, что в силу комплексной сопряженности выражений и , имеет место равенство | |=| |.

Входящая в выражение (37) характеристика представляет собой АФХ для ошибки, которая определяется как

,

где | | - АЧХ для ошибки, - ФЧХ для ошибки.

Как видим, условие селективной инвариантности до ε к гармоническому задающему воздействию выполняется, если значение АЧХ для ошибки ограничено на частоте задающего воздействия.

В соответствии с физическим смыслом любой АЧХ звена (системы) АЧХ для ошибки определяет амплитуду ε₀ установившейся ошибки воспроизведения

на гармоническое задающее воздействие (21), причем

(38)

Следовательно, при выполнении условия (37) амплитуда установившейся ошибки воспроизведения и отсюда сама установившаяся ошибка воспроизведения ограничены, т.е.

При построении систем автоматического управления требуется, чтобы амплитуда ε₀ установившейся ошибки воспроизведения балы не только ограниченной, но и достаточно малой величиной. Обычно это требование записывается в виде

где - допустимая установившаяся ошибка воспроизведения, а определяет диапазон изменения частоты w_v гармонического задающего воздействия, другими словами, спектр задающего воздействия.

Полагая, что максимальная величина v_макс амплитуды v₀ гармонического воздействия известна (v₀ v_макс), с помощью (38) и (33) получаем условие требуемой точности воспроизведения гармонического задающего воздействия

(40)

где - относительная допустимая ошибка воспроизведения. Чем меньше , тем выше точность работы системы управления при низкочастотных задающих воздействиях.

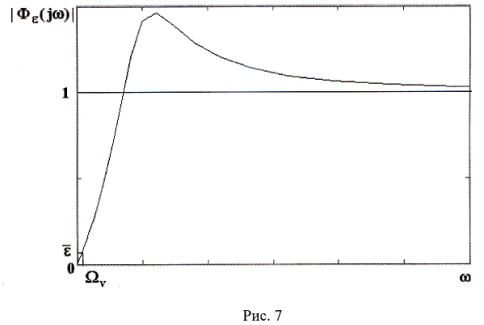
Вывод. Для обеспечения высокой точности работы системы в установившемся режиме надо, чтобы АЧХ для ошибки принимала как можно малые значения в диапазоне частот задающего воздействия. На рис. 7 показана АЧХ для ошибки, соответствующая типичной высокоточной системы управления.

Учитывая, что АФХ замкнутой системы Ф(jw) связана с АФХ для ошибки соотношением

,

приходим к еще одному выводу: точность работы системы тем выше, чем ближе к единице значения АЧХ замкнутой системы в диапазоне частот задающего воздействия, т.е. если

Для системы с единичной обратной связью

(41)

где - АФХ разомкнутой системы, условие требуемой точности воспроизведения гармонического задающего воздействия можно представить в виде

(42)

Здесь учитываем, что при выполнении условия (42) АЧХ разомкнутой системы достигает весьма больших значений в диапазоне частот задающего воздействия, т.е.

(43)

Применительно к ЛАЧХ разомкнутой системы

L(w)=20lg|W(jw)|

условие (42) требуемой точности воспроизведения гармонического задающего воздействия имеет вид

. (44)

Значение определяет нижнюю допустимую границу для ЛАЧХ разомкнутой системы в диапазоне частот задающего воздействия (рис. 8).

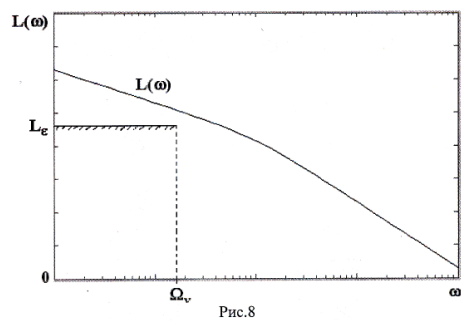
Если ЛАЧХ L(w) проходит ниже допустимой границы, система не удовлетворяет требованиям, предъявленным к точности ее работы в установившемся режиме.

Анализ качества переходного процесса САР при ступенчатом воздействии

При ступенчатом воздействии вида

все переменные устойчивой системы переходят из одного установившегося состояния в другое установившееся состояние. Условия работы системы при таком воздействии весьма неблагоприятны. Поэтому часто, даже когда система не подвержена скачкообразным воздействиям, ее рассчитывают на такой вид воздействия.

Реакция системы на ступенчатую функцию представляет собой переходную характеристику h(t). Чем меньше отличается переходная характеристика от своего установившегося значения, тем выше качество переходного процесса. При этом качество переходного процесса системы определяется как видом характеристики (переходный процесс без перерегулирования, с перерегулированием, монотонный, немонотонный), так и величинами некоторых параметров этой характеристики, носящих название показателей качества. Основными показателями качества являются следующие.

1) Перерегулирование, т.е. величина максимального отклонения от установившегося режима, выраженная в процентах:

2) Время переходного процесса (регулирования) t_p, определяемое моментом, начиная с которого значение управляемой величины отличается от установившегося значения не более, чем на , т.е.

.

Величина обычно лежит в пределах от 0,01 до 0,05.

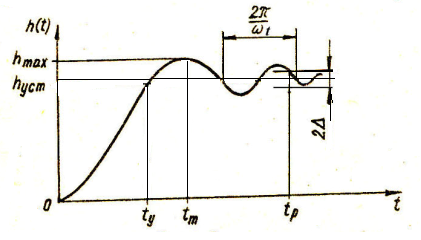
Рис. 5

3) Время установления t_y , определяемое моментом, когда переходная характеристика в первый раз достигает своего установившегося значения.

Перерегулирование определяет запасы устойчивости или, по-другому, колебательность системы, а время регулирования и установления характеризуют быстродействие системы, т.е. скорость, с которой системы переходит от одного установившегося состояния к другому.

Кроме основных показателей качества в ряде случаев используют второстепенные показатели качества: число колебаний за время t_p (обычно в хороших системах), время наступления первого максимума переходной характеристики t_m, круговую частоту колебаний w_t. Для того, чтобы оценить качество системы или определить, удовлетворяет ли система заданным требованиям качества, необходимо сравнить заданные величины , t_p, t_y с теми значениями, которые имеют место в проектируемой системе. Для этого нужно построить переходную характеристику системы.

Косвенные методы оценки качества переходного процесса.

В настоящее время применяются в основном два метода вычисления и построения переходной характеристики: аналитический, основанный на формуле

и используемый, когда известны передаточная функция замкнутой системы Ф(р)=К(р)/Д(р), ее полюсы , и порядок системы небольшой n<3; машинный, опирающийся на современные пакеты Matlab, Vissim.

Методы оценки быстродействия и колебательности систем регулирования, связанные с построением переходной характеристики, получили название прямых методов оценки качества переходного процесса. Применение этих методов является целесообразным на заключительных этапах проектирования системы, т.к. связано с трудностью нахождения переходной характеристики.

На предварительных этапах проектирования системы используют более простые методы оценки качества, позволяющие получить приближенное представление о динамических свойствах системы, не прибегая к вычислению переходного процесса. Косвенные методы оценки качества переходного процесса дают возможность вычислить приближенные значения величин , t_p и t_y либо по виду частотных характеристик системы, либо по расположению нулей и полюсов замкнутой системы.

Частотные методы оценки качества переходного процесса

А) Оценка качества переходного процесса по АЧХ замкнутой системы и АФХ разомкнутой системы.

Система автоматического управления была бы идеальной, если бы выходная величина системы в любой момент времени в точности равнялась бы входной величине. Так как любой входной сигнал может быть представлен в виде суммы синусоидальных составляющих с разными частотами путем разложения в ряд Фурье или представления в виде интеграла Фурье, то в случае идеальной системы амплитуда любой гармоники на выходе должна равняться амплитуде той же гармоники на входе, т.е. АЧХ замкнутой системы, определяемая как

Ф(w)=|Ф(jw)|,

где Ф(jw)=Ф(р)|_p=jw представляет собой АФХ замкнутой системы, должна удовлетворять условию

Ф(w)=1 (83)

для всех частот.

Обычно составляющих очень высокой частоты в задающем воздействии не содержится. Поэтому условие (83) должно выполняться лишь для некоторой полосы частот от 0 до w_cз, а при остальных частотах Ф(w) в соответствии с требованием высокой помехоустойчивости должна обращаться в нуль.

Таким образом, характеристика Ф(w) для идеальной системы должна иметь вид АЧХ идеального фильтра низких частот, показанной на рис. 15.

Характеристика Ф(w) реальной системы отличается от идеальной (рис. 15) наличием максимума Ф_макс и постепенным спадом при высоких частотах. Частота w_p, при которой Ф(w)=Ф_макс, называется резонансной частотой.

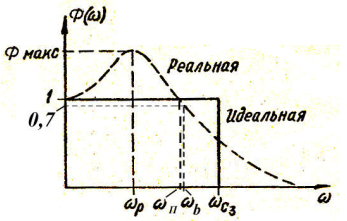
Рис. 15

Сравнивая характеристики реальной и идеальной систем, видим, что различие между этими характеристиками тем больше, чем больше величина М=Ф_макс. Поэтому эта величина, называемая показателем колебательности, может служить для оценки качества переходного процесса, а именно для оценки запаса устойчивости (колебательности) системы. Чем больше М, тем больше колебательность, а следовательно, и перерегулирование. Если М обращается в бесконечность, то это свидетельствует о нахождении системы на границе устойчивости.

Действительно, если модуль характеристики Ф(jw) равен бесконечности, то и само выражение Ф(jw)=∞ на частоте w_p. Следовательно, система имеет два сопряженных мнимых полюса ±jw_р.

Обычно считают, что переходная характеристика имеет слабую колебательность, если величина М не превосходит 1,2-1,5.

Если начальное значение характеристики Ф(w) не равно 1 (это имеет место в случае статических систем), то за показатель колебательности принимают величину относительного максимума Ф_макс/Ф(0).

При Ь>1 время установления t_y можно оценить по формуле

(85)

По этой же формуле можно приближенно оценить время t_m первого максимума переходной характеристики h(t) системы.

Обычно при М=1,1-1,5 круговая частота w_t колебаний переходной характеристики близка к частоте резонанса. Если теперь считать, что число колебаний за время переходного процесса t_p равно двум, то

(86)

О быстродействии можно судить по частотам w_п и w_b, определяющих полосу пропускания замкнутой системы соответственно на уровне 1 и 0,707. Дело в том, что при М=1,1-1,5 w_п и w_b примерно равны резонансной частоте.

От оценок по частотным характеристикам замкнутой системы можно перейти к оценкам по АФХ разомкнутой системы. При этом в качестве оценок фигурируют частота среза w_c и запасы устойчивости по фазе и амплитуде 1/h.

В случае, когда переходная характеристика носит колебательный характер (М>1), частота w_c приблизительно равна частоте w_p. Поэтому время t_y и t_p можно определить по формулам (85) и (86), произведя в них замену w_p на w_c.

Перерегулирование, а следовательно, и колебательность переходной характеристики можно оценить по запасам устойчивости и 1/h, показывающим, насколько удалена АФХ от точки с координатами (-1,j0).

Запас устойчивости можно связать с показателем колебательности М, если аппроксимировать систему высокого порядка системой второго порядка. На возможность такой аппроксимации как первого приближения указано А.Ю.Ишлинским. Графики, представленные на рис. 17 дают количественную связь между перерегулированием , показателем колебательности М, запасом устойчивости по фазе и относительным коэффициентом затухания системы второго порядка с передаточной функцией

.

Из рисунка 17 видно, что приемлемый запас устойчивости по фазе лежит в пределах 30-60^о.

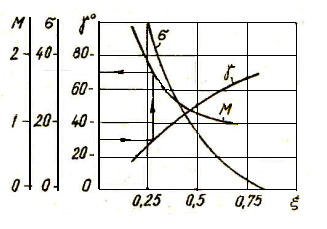
Рис. 17.

В таблице приведены соотношения, связывающие показатели качества с параметрами системы второго порядка.

Кроме того, для такой системы полоса пропускания на уровне 0,707 может быть найдена по приближенной формуле

w_b= (-1.19 +1.85)w₀

Как показала практика, для качественной работы системы требуется запас устойчивости по амплитуде, который лежит в пределах 3-5.

б) Оценка качества переходного процесса по ЛЧХ

Запасы устойчивости по фазе и амплитуде , а также частота среза w_c могут быть найдены с помощью ЛЧХ L(w) и разомкнутой системы. Поэтому все выводы предыдущего раздела, касающиеся вопроса об оценке качества системы с помощью величин , 1/h, w_c, справедливы и в данном случае. Так, приемлемый запас устойчивости по амплитуде определяется рекомендуемыми значениями 1/h и лежит в пределах 10-15 дБ.

Замечание. Перерегулирование обычно более чувствительно к запасу устойчивости по фазе, чем к запасу устойчивости по модулю, т.к. в первом случае разомкнутая система имеет больший коэффициент усиления. Поэтому требования к колебательности системы могут быть заданы в виде одного запаса устойчивости по фазе .

С помощью ЛЧХ можно получить более точную оценку качества минимально-фазовых систем.

Как известно, в минимально-фазовых системах существует однозначная связь между логарифмическими амплитудной L(w) и фазовой характеристиками. Поэтому о свойствах таких систем можно судить, лишь зная одну из этих характеристик. В теории автоматического управления применяют обычно характеристику L(w), имея в виду простоту ее построения.

В основу суждения о поведении замкнутой системы положено понятие типовой ЛАЧХ L(w).

Если ЛАЧХ разомкнутой системы удовлетворяет следующим трем условиям:

- значения ЛАЧХ в низкочастотной области относительно велики с целью обеспечения малой величины установившейся ошибки;

- значения ЛАЧХ в высокочастотной области относительно малы с целью уменьшения влияния высокочастотных помех;

- наклон ЛАЧХ в области средних частот [0,4w_c;4w_c] примерно равен -20дБ/дек, то справедливы следующие соотношения, связывающие показатели качества

.

Здесь М – показатель колебательности, - полоса пропускания, определяемая диапазоном частот, в котором АЧХ замкнутой системы больше или равна единице.

При этом относительный коэффициент затухания и собственная частота колебания w₀, соответствующие паре ближайших к мнимой оси комплексно-сопряженных полюсов замкнутой системы (доминирующих полюсов), определяются как

Оценка качества системы по этим формулам обеспечивает достаточную для практики точность. Так частота w_c косвенно характеризует длительность переходного процесса. Время переходного процесса t_p≈3/w_c при 5% допустимой ошибке обратно пропорционально частоте среза.

Особо отметим, что для малой колебательности (большого запаса устойчивости) системы необходимо, чтобы частота среза w_c приходилась на участок характеристики L(w) с наклоном -20дБ/дек. Причем, чем шире участок с наклоном -20дБ/дек, тем больше запасы устойчивости системы при прочих равных условиях.

Корневые методы оценки качества переходного процесса

Переходную характеристику h(t), представляющую собой переходный процесс при единичном ступенчатом воздействии, можно рассматривать как сумму установившейся h_ycm и переходной h_nep(t) составляющих. Выражение для переходной составляющей зависит от нулей z_j и полюсов p_i замкнутой системы и определяется соотношением

(87)

где

.

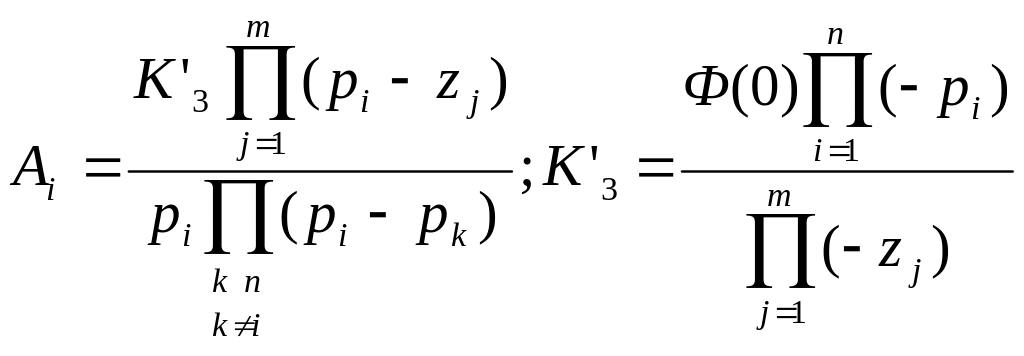При выводе выражения (87) использовалось представление передаточной функции замкнутой системы в виде

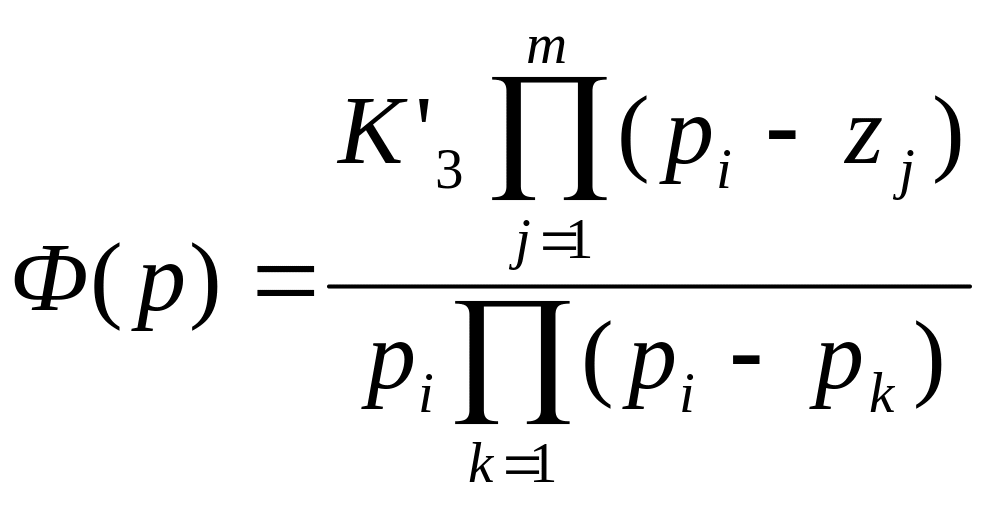
По расположению ее нулей и полюсов можно судить о качестве системы.

Оценка времени переходного процесса.

Время переходного процесса определяется как время, в течение которого переходная составляющая затухает до величины % от своего начального значения. Поэтому для оценки времени переходного процесса необходимо рассмотреть скорость затухания мод системы.

Выражение (87) включает в себя как апериодические составляющие (моды) , соответствующие вещественным полюсам , так и колебательные составляющие (моды) , соответствующие комплексно-сопряженным полюсам . Затухание этих составляющих определяется множителем . При этом чем больше вещественная часть полюса р_i (или сам вещественный полюс), тем быстрее затухает мода.

Корни характеристического уравнения (полюса замкнутой системы) удобно изображать в виде точек на комплексной плоскости (рис. 19), по осям которой отложены вещественная и мнимая части корней. Так как можно говорить только о качестве переходного процесса устойчивой системы, у которой вещественные части всех корней отрицательны, то все корни будут расположены слева от мнимой оси. При этом чем дальше от мнимой оси расположены корни р_i=- и , тем большему значению они соответствуют.

Наиболее медленно будет затухать мода , имеющая наименьшее . Поэтому можно приближенно считать, что скорость затухания переходного процесса определяется такой модой , которая соответствует корням наиболее близко расположенным к мнимой оси. Величина , наименьшая из всех значений , являющихся вещественными частями корней характеристического уравнения Д(р)=0, называется степенью устойчивости и обозначается (рис. 19).

Эта величина позволяет приближенно оценить время переходного процесса при 5% -допустимой ошибке

(89)

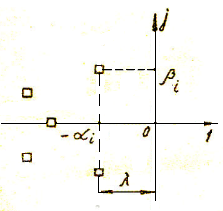
Рис. 19

Оценка перерегулирования.

Перерегулирование системы зависит от поведения колебательных составляющих

,

так как колебательные процессы в системе будут наблюдаться только в том случае, когда характеристическое уравнение содержит комплексно-сопряженные корни . Склонность системы к колебаниям характеризует оценка

,

которую называют колебательностью.

Таким образом, чем больше величина , тем более колебательный характер будут иметь переходные процессы и наоборот. В пределе при =∞ полюса системы будут «чисто» мнимыми, и в ней будут наблюдаться переходные процессы в виде незатухающих колебаний. В случае, когда =0, все корни характеристического уравнения будут вещественными и в системе будут возникать апериодические процессы. Эмпирическим путем установлена взаимосвязь между колебательностью и перерегулированием в виде соотношения

.

Отметим, что при значение перерегулирования в системе составит .

Связь колебательности и относительного коэффициента затухания определяется формулой

.

Рассмотренные корневые методы оценки не учитывают влияние на постоянные коэффициенты А_i других нулей и полюсов замкнутой системы, наличие которых, как это видно из выражения (87), может существенно изменить качество переходного процесса.

Анализируя выражение (87), можно сделать следующие выводы относительно влияния расположения нулей и полюсов на вид и характер переходной характеристики.

1) Основное влияние на качество переходного процесса оказывает группа ближайших к мнимой оси нулей и полюсов (так называемых доминирующих нулей и полюсов).

2) Длительность переходного процесса в основном определяется степенью устойчивости системы, равной абсолютному значению вещественной части ближайших к мнимой оси комплексных полюсов замкнутой системы или вещественного полюса, если он является ближайшим к мнимой оси. При этом длительность переходного процесса может быть определена по формуле (89).

3) Величина перерегулирования зависит от степени колебательности доминирующих комплексных полюсов и от степени близости к мнимой оси остальных нулей и полюсов замкнутой системы.

4) Близкие к мнимой оси нули увеличивают перерегулирование, а близкие (но не доминирующие) полюсы его уменьшают.

Не останавливаясь на доказательстве всех этих пунктов, приведем лишь соображения, подтверждающие вывод об увеличении перерегулирования при введении в систему нулей.

Пусть САУ описывается в отсутствии нулей передаточной функцией Ф₀(р). Введем в эту систему нуль z=- , так чтобы при этом не изменился коэффициент усиления замкнутой системы k_з=Ф₀(р). Тогда передаточная функция примет вид

По изображению

найдем переходную характеристику полученной системы

,

как сумму переходной характеристики исходной и взвешенной производной этой характеристики.

В начале переходного процесса характеристика h(t) возрастает с большой скоростью и поэтому ее производная h’₀(t) положительна и имеет большую величину. В результате сложения кривых h₀(t) и получается кривая h(t), имеющая увеличенное перерегулирование, причем перерегулирование увеличивается тем значительнее, чем меньше абсолютное значение нуля передаточной функции Ф(р).

Введение большего числа нулей приводит к тому же эффекту.

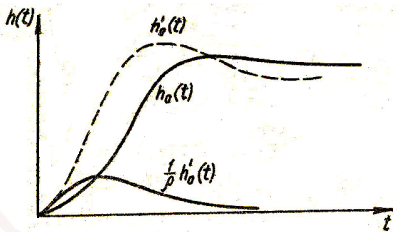
Рис. 24

Для системы второго порядка с комплексно-сопряженными полюсами введение нуля увеличивает перерегулирование при а<4.

Чувствительность систем управления к изменению параметров

Объект управления, представленный передаточной функцией W(p), какова бы ни была его природа, подвержен влиянию окружающей среды, старению, отсутствию точной информации о его параметрах и других объективных факторов, которые негативно сказываются на его поведении. В разомкнутой системе все эти факторы приводят к отклонению выходной переменной от желаемого значения. Замкнутая система, напротив, чувствует это отклонение, обусловленное изменениями параметров объекта, и пытается скорректировать выходную переменную. Поэтому чувствительность системы управления к изменению параметров есть вопрос первостепенной важности. Основное преимущество систем с обратной связью состоит в их способности снижать чувствительность к изменению параметров.

В случае замкнутой системы, если W(p)>>1 для всех представляющих интерес значений частоты, то из

Ф(р)=W(p)/|1+W(p)| (1)

мы имеем

Y(p)≈V(p).

Следовательно, мы в точности достигаем желаемого результата, т.е. выход становится равным входу. Однако прежде чем использовать эту идею для построения системы управления, мы должны заметить, что условие W(p)>>1 может привести к тому, что реакция системы будет сильно колебательной или даже к потере системой устойчивости. Но, тем не менее, тот факт, что увеличивая модель функции |W(p)|, мы уменьшаем влияние изменений в W(p) на выходную переменную, является исключительно ценным. Таким образом, важным преимуществом системы с обратной связью является то, что в ней уменьшается влияние изменений параметров объекта управления.

Чтобы проиллюстрировать сказанное выше, рассмотрим случай, когда за счет изменений параметров объекта его передаточная функция приняла выражение . Тогда, если система является разомкнутой, выходная переменная ( в виде изображения по Лапласу) получит приращение

.

В замкнутой системе мы имеем

. (1а)

Отсюда приращение выходной переменной:

.

Если , как это часто имеет место, то

. (2)

Анализ выражения (2) показывает, что в замкнутой системе изменение выходной переменной уменьшается в [1+W(p)] раз; в свою очередь член [1+W(p)] обычно много больше единицы в представляющем интерес диапазоне комплексной частоты. Сомножитель 1+W(p) играет очень важную роль в определении характеристик систем с обратной связью.

Чувствительность системы определяется как отношение процентного изменения передаточной функции системы к процентному изменению передаточной функции объекта. Система имеет передаточную функцию

Ф(р)=Y(р)/V(p),

и, следовательно, чувствительность определяется, как

. (3)

В пределе, переходя к малым изменениям, (3) приводится к виду:

. (4)

Чувствительность системы – это отношение изменения ее передаточной функции к изменениям передаточной функции (или параметров) объекта управления при условии их малости.

Из (1а) следует, что чувствительность разомкнутой системы равна единице. Чувствительность замкнутой системы легко можно получить из (4). Замкнутая система имеет передаточную функцию

.

Следовательно, ее чувствительность равна

или

. (5)

Отсюда еще раз видно, что чувствительность замкнутой системы можно сделать меньше, чем ее чувствительность в разомкнутом состоянии, путем увеличения W(p) в представляющем интерес диапазоне частот.

Часто бывает необходимо определить чувствительность , где - параметр передаточной функции W(p). Используя правило дифференцирования сложной функции, можно записать:

.

Встречаются также случаи, когда передаточная функция системы Ф(р) имеет вид дроби:

,

где - параметр, подверженный изменениям за счет внешних факторов. Тогда чувствительность системы к изменению можно записать, используя выражение (4):

,

где - номинальное значение параметра.

Способность уменьшать влияние изменения параметра путем введения обратной связи – одно из положительных качеств замкнутых систем управления. Чтобы добиться высокой точности управления в разомкнутых системах, необходимо очень тщательно подходить к выбору элементов, образующих передаточную функцию W(p). Напротив, замкнутые системы допускают определенные вариации параметров W(p), поскольку их влияние ослабляется в (1+W(p)) раз.