Коррекция системы с помощью опережения по фазе (реальный пд-регулятор)

а) КУ с опережением по фазе

Его ПФ:

Параметры КУ:

q₁=T, q₂=α, q₃=k₂, α<1,

где 1/α – коэффициент опережения по фазе.

Построим ЛЧХ КУ.

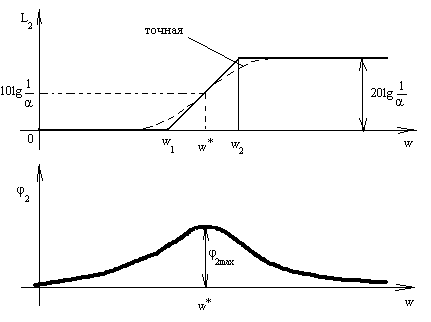
Положим k₂=1. Найдем сопрягающие частоты:

w₁=1/T, w₂=1/αT w₂>w₁

Так как

,

то .

Выражение для ЛФЧХ

φ₂(w)=arctgwT- arctgαwT.

Известно, что

.

Полагая x=wT, y=αwT, получаем

.

Дифференцируя φ₂(w) по w, находим

(*)

и максимум

(**)

График зависимости изображен на рисунке:

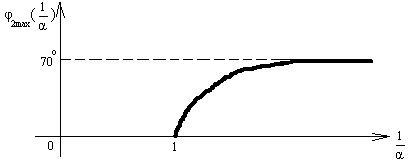
Если α=0, то - ПД-регулятор.

Необходимо выбрать α и Т.

б) Выбор параметров α и Т корректирующего устройства с опережением по фазе.

Пусть заданы требуемые значения коэффициента усиления k* и запаса устойчивости по фазе γ*.

Изменим k₁ так, чтобы коэффициент усиления скорректированной системы был равен требуемому значению k*,т.е., чтобы выполнялось условие: k=k*.

1. Построим ЛЧХ нескорректированной системы L₁(w) и φ₁ (w) и определим запас устойчивости по фазе

γ₁=π+φ₁(w_c),

где w_c – частота среза нескорректированной системы. Нескорректированная система при высоких значениях k₁ оказывается неустойчивой или весьма колебательной, т.е. γ₁<γ*.

2. Определим разность между γ₁ и γ*

.

3. Выбираем параметр α из условия

,

используя для этой цели формулу (**) для или графическую зависимость .

4. Определим частоту среза скорректированной системы wc*, исходя из .

5. Полагая w*=w_c*, находим параметр и частоты w₁=1/T, w₂=1/αT.

6. По формулам

строим ЛЧХ скорректированной системы и определяем, удовлетворяет ли система требованиям с точки зрения запаса устойчивости по фазе.

. Действительно, если вычисления выполнены точно,

,

то L(w) должна пересекать ось w при w=w_c*,

так что w_c*=w*.

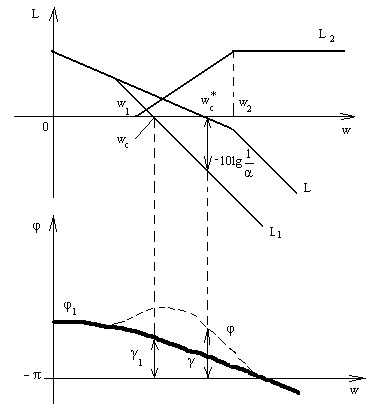
Максимальный сдвиг по фазе должен быть при w_c*. Если , то процесс синтеза заканчивается, если нет, то необходимо варьировать параметры.

Достоинства:

1. КУ с опережением по фазе не затрагивает низкочастотного участка ЛАЧХ, т.е. не влияет на заданную точность работы системы в установившемся режиме.

2. Добились желаемого запаса устойчивости по фазе γ*

3. w_c*>w_c , следовательно увеличивается полоса пропускания (ПП) и увеличивается быстродействие

Недостатки:

1. Увеличение полосы пропускания ведет за собой снижение помехоустойчивости.

2. Увеличение быстродействия связано с увеличением управляющего воздействия u(t), что может повлечь за собой выход системы из строя или заставить работать систему в нелинейном режиме. Поскольку при синтезе все элементы предполагались линейными, то влияние нелинейностей в рамках линейной теории оценить невозможно.

Техническая реализация КУ с опережением по фазе

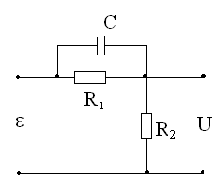
Коэффициент усиления нескорректированной системы надо увеличить в 1/α, чтобы включение цепи не повлекло за собой уменьшение коэффициента усиления системы.

Коррекция с помощью КУ с отставанием по фазе

а) КУ с отставанием по фазе

ПФ имеет тот же вид, что и для КУ с опережением по фазе:

,

однако α>1.

Найдем сопрягающие частоты w₁=1/αT, w₂=1/T, причем w₂>w₁

Положим k₂=1.

ЛЧХ КУ с опережением по фазе L₂(w), φ₂(w) (см. рисунок ниже) представляют собой зеркальное отображение относительно оси частот ЛЧХ КУ с отставанием по фазе.

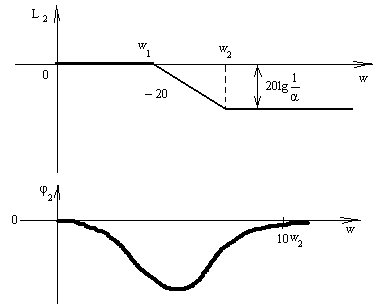
φ₂(10w₂)=-5^о

Параметры α и Т надо выбрать таким образом, чтобы система удовлетворяла заданным требованиям k* и γ*. Выберем k₁=k* для обеспечения требуемой точности.

б) Алгоритм синтеза:

1. Построить L₁(w) и φ₁(w) и проверить, удовлетворяет ли нескорректированная система требованиям, предъявляемым к запасу устойчивости по фазе. Если запас устойчивости γ₁=π+φ₁(w_c) недостаточен, перейти к п.2.

2. Выбрать частоту среза w_c* скорректированной системы, исходя из условия φ₁(w_c*)=-π+γ*+5^о. При этом учитываем (см. п.3), что на данной частоте КУ создает дополнительный фазовый сдвиг φ₂(w_c*)=-5^о, так что запас устойчивости скорректированной системы

γ=π+φ(w_c*)=π+φ₁(w_c*)+φ₂(w_c*)= γ*

будет равен требуемому значению.

3. Выбираем параметр Т=10/ w_c* из условия w₂=0,1 w_c*, чтобы гарантировать, что КУ добавит только -5^о к результирующей ЛФЧХ скорректированной системы на частоте w_c*.

4. Выбираем α=|W₁(jw_c*)|, чтобы ЛАЧХ скорректированной системы пересекала ось частот при w_c*. Действительно, при этом

L(w_c*)=L₁(w_c*)+L₂(w_c*)=20lg|W₁(j w_c*)|+20lg|W₂(j w_c*)|=

=20lgα+20lg(1/α)=0.

Теперь можно найти w₁=w₂/α.

5. Используя L=L₁+L₂, φ=φ₁+φ₂, построим ЛЧХ скорректированной системы.

Здесь L₁, φ₁ – ЛЧХ нескорректированной системы

Так как k=k₁=k*, то вид L(w) в области низких частот удовлетворяет заданным требованиям к точности системы.

Если , то процедура выбора параметров заканчивается.

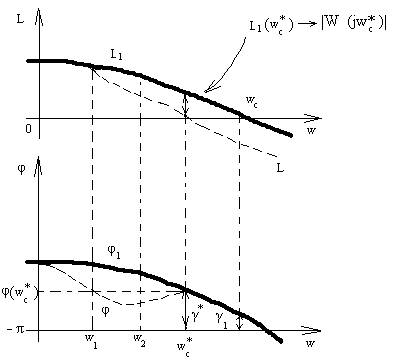
Достоинства:

1. Удалось обеспечить требуемое значение коэффициента усиления k=k* в области низких частот.

2. Обеспечили требуемый запас устойчивости γ*

3. w_c*<w_c – введение этого устройства повышает помехоустойчивость.

Недостатки:

1. Уменьшается полоса пропускания, следовательно, снижается быстродействие за счет того, что w_c*<w_c, затягивается переходный процесс.

2. Возникает проблема пи реализации КУ с отставанием по фазе с помощью RC-схемы, изображенной на рисунке и описываемой ПФ

где

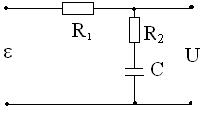
Дело в том, что при больших значениях Т, резистор R₁ должен иметь номинал, превышающий десятки Мом. Это большая величина, поэтому проектировщику не рекомендуется выбирать частоту w₂ КУ далее, чем на одну декаду левее частоты w_c*.

Коррекция с помощью ПИ-регулятора

ПФ Пи-регулятора характеризуется двумя параметрами k₂ – коэффициент усиления и Т – постоянная времени.

Сопрягающая частота w₂=1/T, обычно w₂>k₂, так что k₂T<1.

ПФ скорректированной системы при введении ПИ-регулятора

В ПФ скорректированной системы входит ПФ интегрирующего звена, следовательно, повышается степень астатизма на 1 ν=ν₁+1, что повышает точность работы в установившемся режиме. Здесь ν – порядок астатизма скорректированной системы, а ν₁ - нескорректированной системы.

Если ν₁=0, то статическая ошибка становится равной нулю, т.е. ε_ст=0. Если ν=1, то ε_ст=ε_ск=0.

Построим ЛЧХ этого регулятора.

Так как

,

то .

ЛФЧХ КУ определяется выражением

φ₂(w)=-π/2+arctgwT

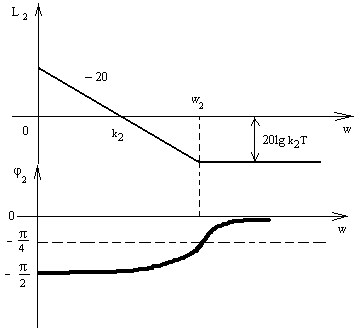
Регулятор с отставанием по фазе близок к ПИ-регулятору. Если увеличить α в регуляторе с отставанием по фазе, то его свойства приблизятся к свойствам ПИ-регулятора.

Выбор параметров ПИ-регулятора:

Пусть требуется повысить порядок астатизма нескорректированной системы на единицу и обеспечить заданный запас устойчивости по фазе γ*.

Алгоритм синтеза:

1) Строим характеристики нескорректированной системы L₁(w) и φ₁(w).

2) Находим w_c* из формулы

φ₁(w_c*)=-π+γ*+5^о

3) w₂ выбирается из условия w₂=0.1w_c*

Отсюда можно найти Т=10/ w_c*

4) k₂ выбирается из условия k₂=1/T|W(j w_c*)|

Это условие гарантирует, что ЛАЧХ скорректированной системы L(w) пересекает ось частот при частоте w_c*.

5) Строим характеристики скорректированной системы

Добавим в п.2 5^о, чтобы .

Все достоинства и недостатки ПИ-регулятора совпадают с регулятором с отставанием по фазе, кроме одного достоинства – повышение порядка астатизма.

Часто в промышленности используют ПИД-регуляторы. Реальный ПИД-регулятор –это последовательное соединение ПИ-регулятора и КУ с опережением по фазе, но с малым значением α ≈ 0. КУ с опережением по фазе дает увеличение запаса устойчивости по фазе, повышает быстродействие.

Робастные САУ

САУ действует в условиях возмущений. Нужно построить систему так, чтобы она была работоспособной даже тогда, когда на нее действует неопределенные возмущения.

Робастная система – система малочувствительная к возмущениям, грубая, надежная, гибкая система.

Свойства робастной системы:

1) Малая чувствительность к небольшим изменениям математической модели объекта управления, ее параметров.

2) Робастная устойчивость

Система, обладающая этим свойством, является устойчивой при конечных вариациях математической модели.

3) Робастное качество

Система является не только устойчивой при изменении математической модели ОУ, но и нормально функционирует, т.е. показатели качества не выходят за допустимые пределы.

Целью синтеза робастных систем является гарантия требуемого качества независимо от погрешностей и изменений параметров модели, несмотря на существенную неопределенность характеристик ОУ.

Обеспечение робастной устойчивости.

В настоящее время все большее внимание при проектировании САУ уделяется проблеме обеспечения робастной устойчивости. Исследование робастной устойчивости в последнее время становится стандартным признаком высокого качества проведения проектно-конструкторских работ, поскольку работоспособность реальных систем в значительной мере определяется их способностью сохранять свои свойства при заранее неопределенных вариациях математических моделей входящих в них динамических объектов или условий их функционирования.

Рассмотрим основные понятия теории робастной устойчивости.

Пусть при исследовании некоторого объекта, подлежащего управлению, была получена его номинальная математическая модель – так называемая номинальная передаточная функция. Номинальная передаточная функция объекта управления имеет вид W₁(p), также имеется некоторый регулятор с передаточной функцией W₂(p). При этом регулятор W₂(p) обеспечивает только номинальную устойчивость как разомкнутой системы с номинальной передаточной функцией

W(p)=W₁(p)W₂(p) (1)

так и замкнутой системы с номинальной передаточной функцией

(2)

Структурная схема номинальной системы представлена на рис.1.

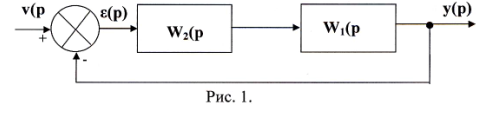
Все реальные системы обладают свойствами, отличными от номинальной модели, так что саму номинальную модель надо рассматривать как обладающую модельной неопределенностью. Как мы уже отмечали, робастная устойчивость имеет отношение к устойчивости для всех моделей в рамках модельной неопределенности. Критерий Найквиста может быть использован для суждения о робастной устойчивости, если рассматривать модельную неопределенность как частотную функцию, которая оценивает уровень модельной неопределенности для каждого значения частоты. Такую частотную функцию называют возмущением номинальной модели или ошибкой моделирования. Итак, передаточная функция реального объекта или, как говорят, возмущенного объекта отличается от номинальной W₁(p) на величину возмущения.

Абсолютным возмущением номинальной передаточной функции объекта управления W₁(p) называется рациональная дробь вида

,

называемая также абсолютной ошибкой моделирования.

Считаем, что абсолютное возмущение имеет только левые полюса, то есть не влияет на устойчивость разомкнутой возмущенной системы, описываемой передаточной функцией

.

Рациональная дробь вида

входящая в последнее выражение, называется относительным возмущением номинальной передаточной функции объекта управления или относительной ошибкой моделирования.

При анализе робастной устойчивости предполагается, что существует множество

,

где A(w) – некоторая известная неотрицательная вещественная частотная функция, характеризующая уровень неопределенности номинальной модели на всех частотах, принадлежащих диапазону .

Возмущенная замкнутая система, описываемая возмущенной передаточной функцией

называется робастно устойчивой, если для всех неопределенностей, принадлежащих множеству D, она является устойчивой, то есть если ее характеристическое уравнение

имеет только левые корни.

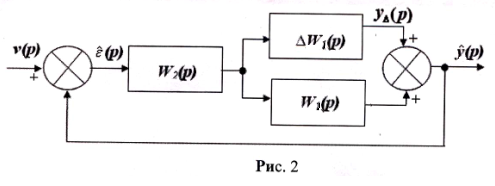
Найдем критерий робастной устойчивости. С этой целью преобразуем структурную схему возмущенной системы, представленную на рис.2, в структурную схему эквивалентной системы, которая в разомкнутом состоянии состоит из последовательного соединения звеньев.

Из структурной схемы (рис.2) следует, что изображение ошибки возмущенной системы имеет вид:

.

Отсюда после несложных преобразований получаем

,

где

.

Согласно двум последним выражениям составим структурную схему эквивалентной системы (рис.3)

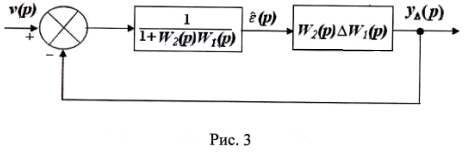
Передаточная функция разомкнутой эквивалентной системы, представленной на рис.3, имеет вид

Умножив и разделив эту передаточную функцию на W₁(p), получим следующее выражение

Следовательно, .

Все полюсы левые, так как по условию Ф(р) и имеют только левые полюса. отсюда разомкнутая эквивалентная система является устойчивой.

АФХ разомкнутой эквивалентной системы имеет вид

,

где Ф(jw) – АФХ номинальной замкнутой системы.

Согласно достаточному условию критерия Найквиста замкнутая эквивалентная, следовательно, замкнутая возмущенная система будут устойчивы, если АФХ разомкнутой эквивалентной системы не будет выходить за пределы или касаться окружности единичного радиуса, т.е. если выполняется условие

,

которое можно записать как

.

Последнее неравенство называют теоремой о малом коэффициенте усилкния. Его (неравенство) можно представить в виде условия

,

которое называют критерием робастной устойчивости. Здесь величина

как говорят, определяет частотную границу робастной устойчивости.

Этот критерий можно записать в логарифмическом виде:

,

где - ЛАЧХ неопределенности, - ЛАЧХ замкнутой номинальной системы.

Критерий робастной устойчивости в большинстве случаев выполняется в области низких и средних частот, поэтому при исследовании робастной устойчивости систем особое внимание следует уделить области высоких частот (области моделируемой динамики). В высокочастотной области АЧХ разомкнутой системы |W(jw)| значительно меньше единицы, поэтому АЧХ замкнутой системы |Ф(jw)| мало отличается от |W(jw)|, так что

|Ф(jw)|=|W(jw)|.

При этом критерий робастной устойчивости применительно к частотам, значительно превышающим частоту среза w_c, можно записать как

|W(jw)||∆(jw)|<1, w>>w_c.

Отсюда для обеспечения робастной устойчивости ЛАЧХ номинальной разомкнутой системы

L(w)=20lg|W(jw)|

на высоких частотах должна проходить ниже логарифмической частотной функции неопределенности L_∆(w)=20lg|∆(jw)|, взятой с отрицательным знаком, т.е. должно выполняться условие

L(w)<-L_∆(w), w>w_s.

Здесь частота w_s является той частотой, при которой логарифмическая частотная характеристика -L_∆(w) пересекает ось частот.

Пример.

Пусть возмущенная ПФ объекта управления, учитывающая неопределенность динамики объекта на высоких частотах, имеет вид

,

где - номинальная ПФ объекта управления. При этом абсолютное возмущение ПФ определяется выражением

Отсюда асимптотическая ЛАЧХ неопределенности, определяемая как

,

построенная по и взятая с отрицательным знаком, представлена на рис.4.

187