§ 65. Обходы

Определения эйлеровых и гамильтоновых ориентиро-анных графов сходны с аналогичными определениями ля неориентированных.

Цепь, содержащая каждую дугу орграфа, называется эйлеровой. Связный орграф называется эйлеровым, если нем есть замкнутая эйлерова цепь.

Следующие две теоремы, характеризующие эйлеровы графы, доказываются так же, как и в неориентированым случае.

Теорема 65.1. Для связного ориентированного графа G следующие утверждения равносильны:

1) граф G эйлеров;

2) для любой вершины v <= VG верно равенство D(v) = d^-(v);

3) граф G является объединением контуров, попарно имеющих общих ребер.

Теорема 65.2. Связный орграф G содержит открытую эйлерову цепь тогда и только тогда, когда в нем есть такие вершины v₁ и v₂, что

d⁺(vi) = d^-( v₁)+1, d+(v₂)=d^-(v₂)-1

d⁺(v) = d^-(v) для любой вершины v, отличной от v₁ и v₂ .

Контур (путь) орграфа G называется гамильтоновым, если он содержит все вершины G. Гамилътонов орграф — это орграф, имеющий гамильтонов контур. Вопросы, связанные с распознаванием гамильтонового орграфа и построением гамильтоновых контуров или сетей, являются столь же сложными, как и аналогичные вопросы для неориентированных графов. Докажем одно достаточное условие гамильтоновости орграфа.

Теорема 65.3 (М. Мейниел, 1973 г.). Пусть G — сильный орграф порядка n>1 без петель и параллель­ных дуг. Если для любой пары и и v его несовпадающих несмежных вершин справедливо неравенство deg и + deg v > 2п — 1, то в G есть гамильтонов контур.

Для доказательства этой теоремы проделаем некото­рую предварительную работу.

Если v<=VG, S VG, то через E(v->S) обозначим множество дуг орграфа G с началом v и концом в S, а через Е(и, S) — множество дуг между и и S, т. е. дуг вида (v, s) или (s, v), где s S.

Как и выше, множество вершин произвольного пути Р будем обозначать через VP.

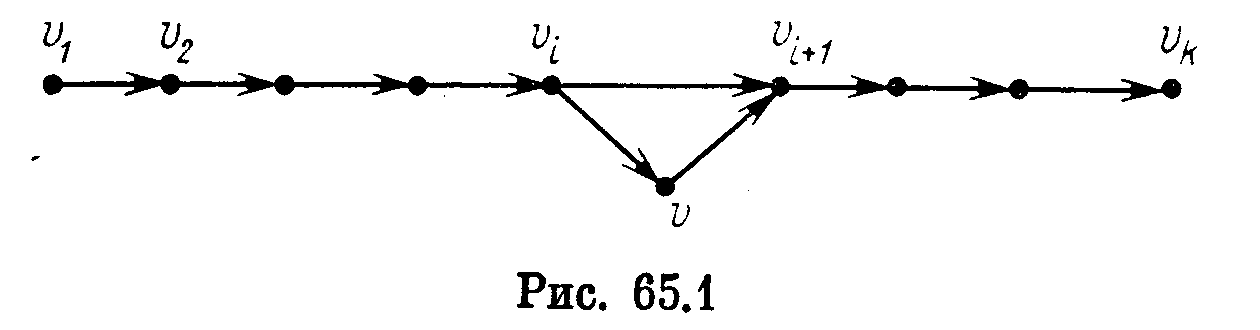
Лемма 65.4. Пусть P = { v₁, v₂, ..., v_k) — путь в ор­графе G, v<=VG\VP, и пусть в G нет (v₁, и_к)-пути, мно­жество вершин которого совпадает с VP U v. Тогда |Е(и, VP)|<k+L

> Для любого i, 1<i<k-1, положим

Очевидно, что

иначе в G существовал бы путь, запрещенный условием леммы (рис. 65.1). Суммируя неравенства (1) по всем i = (1, к — 1) и учитывая при этом возможность существо­вания каждой из дуг (v, v₁) и (v _к, v), получим

Пусть U s VG. Путь Р в орграфе G назовем U-путем, если он удовлетворяет следующим трем условиям:

1) длина пути Р не меньше чем 2;

2) начальная и конечная вершины пути Р принадле­жат множеству U;

3) никакая из других вершин, входящих в Р, не при­надлежит множеству U.

> Теперь перейдем к доказательству теоремы 65.3, которое проведем от противного. Пусть орграф G удовлет­воряет условиям теоремы и не является гамильтоновым и пусть S = (v₁, v₂, ..., v_k, v₁)—такой контур в G, мно­жество вершин которого не является собственным под­множеством множества вершин другого контура. Рассмот­рим отдельно два случая.

1) В G нет VS-путт. Возьмем какие-либо две верши­ны — одну в S, а другую — вне S. В сильном орграфе G есть контур S', содержащий эти две вершины и потому отличающийся от S.

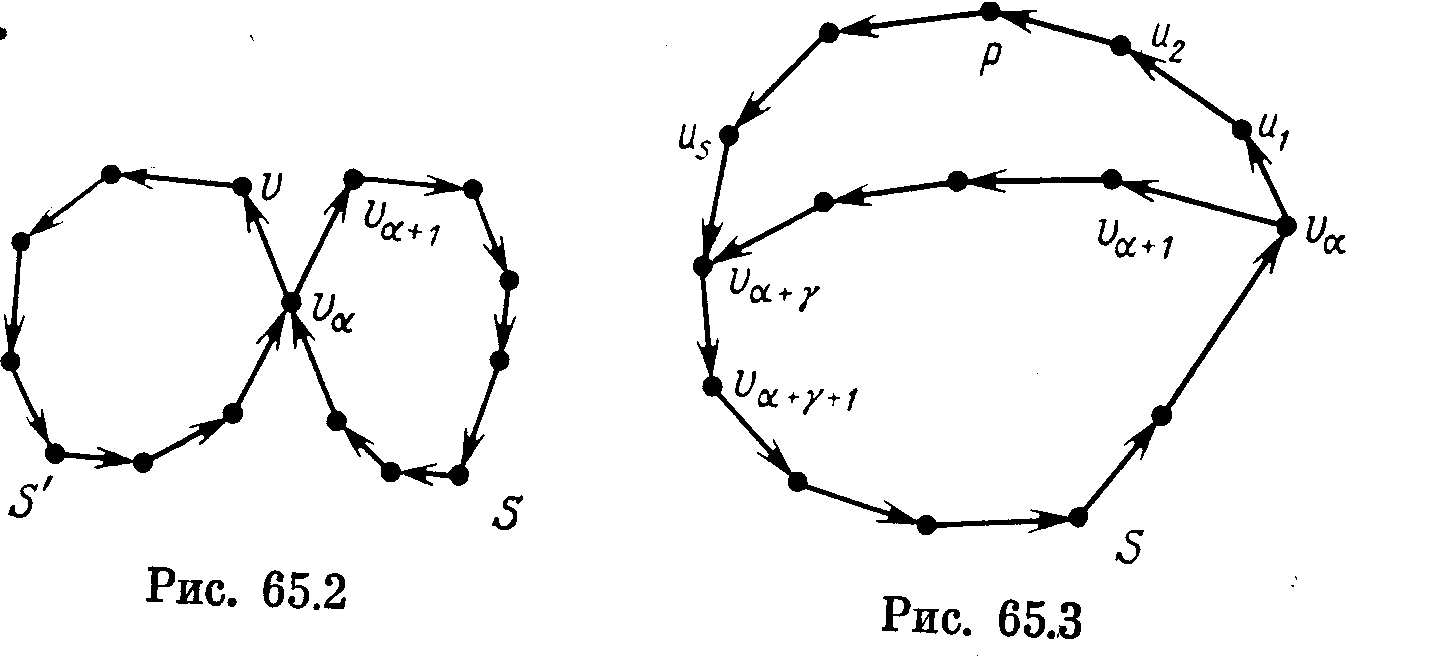
Эти два контура имеют ровно одну общую вершину, скажем, v_a, иначе в G был бы VS-путь. Пусть теперь v_a+1 и v — вершины, непосредственно сле­дующие за v_a в контурах S и S' соответственно (рис. 65.2). Так как в орграфе G нет VS-путей, то вершина v не смежна ни с одной из вершин, входящих в S и отличных от v_a. По той же причине для любой вершины и VG\(VSU v) верно неравенство |Е(и, {v_a+1 ,v})|<2. Следовательно, для несмежных вершин v и v_a+1 имеем

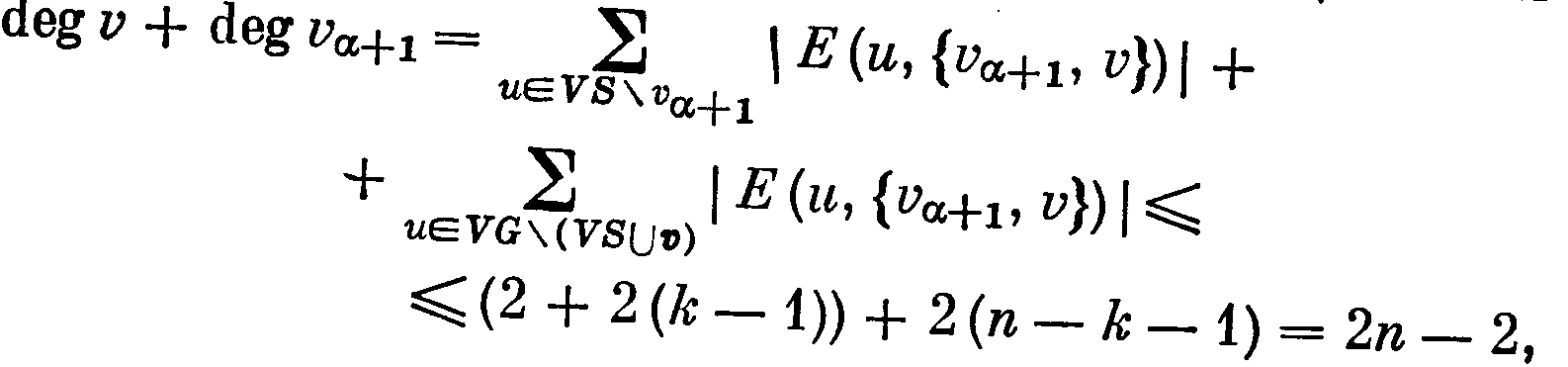
что противоречит условию теоремы (здесь первая сумма учитывает дуги, соединяющие вершины v_a+1 и v с вер­шинами из VS, а вторая —дуги, соединяющие и_а+1 и v с остальными вершинами графа).

2) В орграфе G есть VS-nymи Выберем среди них путь

P = (v_a, и₁, и₂, ..., и_а, V_a+ γ) с минимальным γ (см. рис. 65.3). Из максимальности контура S следует, что γ > 1. Определим β как макси­мальное среди таких чисел i, что 1 < i < γ и в G есть (V_a+ γ , V_a)-путь Р', для которого

VP' = VS\{v_a+i, ..., v_a+ γ -1}

(возможно, β = 1 и тогда Р' = (v_a+ γ, v_a+ γ _+1, …., v_a). Та­ким образом, |VP'| = к — β + γ. Так как PUP' также яв­ляется контуром, из максимальности контура S вытекает, что (} < у. Из выбора числа β следует, что в G нет (V_a+ γ , V_a)-пути с множеством вершин VP' U (v_a+t), так что в силу леммы 65.4 вершина v_a+β соединена с Р' не более чем к — β + γ + 1 дугами.

Пусть Р" =(v_a+ γ, v_a+ γ _+1, …., v_a).. Так как контур S максимален, то в G нет (v_a+i, v_а)-пути с множеством вер­шин VP" U и₁. Из леммы 65.4 теперь следует, что верши­на и₁ соединена с Р" не более чем к — γ + 2 дугами.

Из минимальности числа γ вытекает, что и₁ не смеж­на ни с какой вершиной v_a+1, 1< i <γ, и что для любой вершины и VG\(VSU и₁) выполняется неравенство

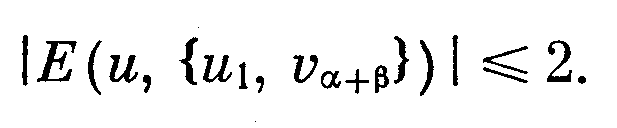
Учитывая вышесказанное, получаем для несмежных вершин и₁ и v_a+β

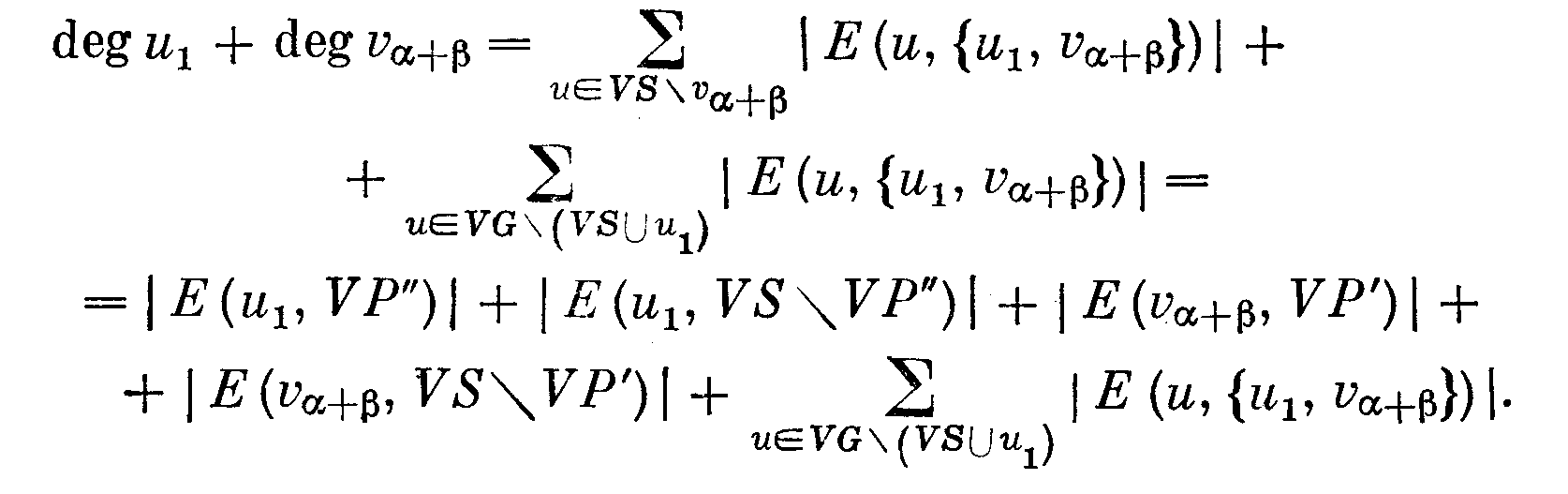
Учитывая полученные выше соотношения, а также то, что

и в графе могут существовать дуги вида (v_a+β, v_a+i), (v_a+i,v_a+β), 1< i <γ получаем

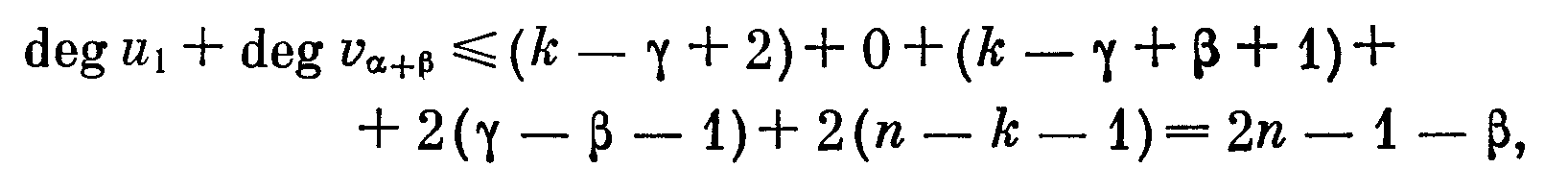
что противоречит условию теоремы. <

Очевидно

Следствие 65.5. Сильный орграф порядка п без петель и параллельных дуг, степень каждой вершины ко­торого не менее п, имеет гамилътонов контур.