27. Несобственные интегралы, критерий Коши сходимости несобственных интегралов. Признаки сходимости: признак сравнения, признаки Абеля и Дирихле.

Понятие несобственного интеграла первого рода.

Одномерными связными неограниченными областями являются полупрямые a≤x<+∞, -∞<x≤b и бесконечная прямая -∞<x<+∞. Ради определенности рассмотрим полупрямую a≤x<+∞.

Будем предполагать, что функция f(x) определена на полупрямой a≤x<+∞ и для любого R≥a существует определенный интеграл , который мы обозначим символом F(R):

F(R)= . (1)

Итак, при наших предположениях на полупрямой a≤R<+∞ задана функция F(R), определенная соотношением (1). Исследуем вопрос о предельном значении функции F(R) при R→+∞, т.е. вопрос о существовании предела lim .(2)

Для выражения (2) мы будем использовать обозначение . (3)

В дальнейшем символ (3) мы будем называть несобственным интегралом первого рода от функции f(x) по полупрямой a≤x<+∞.

Если существует предел (2), то несобственный интеграл (3) наз. сходящимся. Если же этот предел не существует, то несобственный интеграл наз. расходящимся.

Зам.1. Рассмотрим несобственный интеграл (3). Если b>a, то наряду с этим интегралом можно рассматривать интеграл . Очевидно, из сходимости одного из указанных интегралов вытекает сходимость другого. При этом имеет место следующее равенство: = .

Отметим, что расходимость одного из указанных несобственных интегралов влечет расходимость другого.

Зам.2. Если несобственный интеграл (3) сходится, то значение предела (2) обозначается тем же символом (3). Таким образом, в случае сходимости интеграла (3) используется равенство

при R→+∞.

Зам.3. Аналогично несобственному интегралу (3) определяются несобственные интегралы и . Первый из них символизирует операцию предельного перехода lim (R→-∞), а второй - lim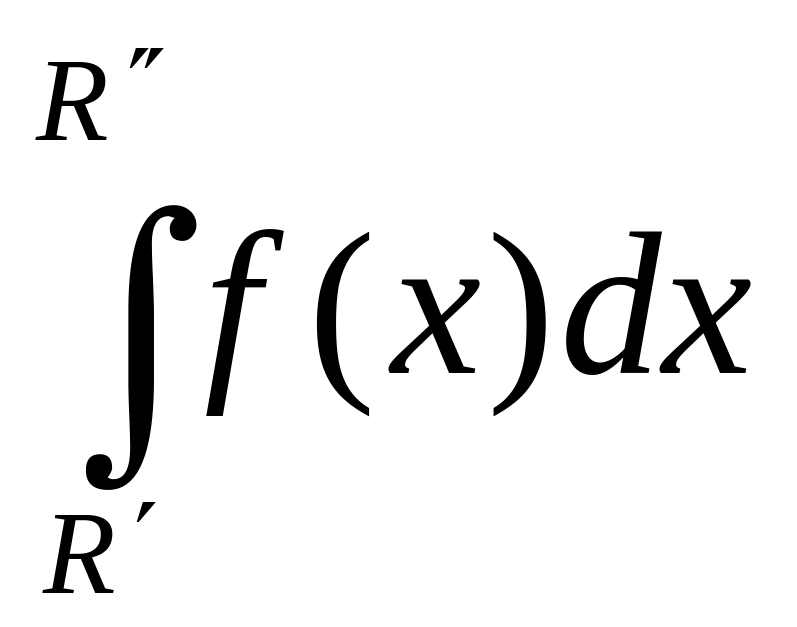 (R’→−∞, R”→+∞).

Критерий Коши сходимости несобственного интеграла первого рода. Достаточные признаки сходимости.

Вопрос о сходимости несобственного интеграла первого рода эквивалентен вопросу о существовании предельного значения функции F(R)= при R→+∞. Как известно, для существования предельного значения функции F(R) при R→∞ необходимо и достаточно, чтобы она удовлетворяла следующему условию Коши: для любого ε>0 можно указать такое А>0, что для любых R’ и R”, превосходящих А, выполняется неравенство . Таким образом, справедливо следующее утверждение.

Теорема 1.(критерий Коши сходимости несобственного интеграла). Для сходимости несобственного интеграла (3) необходимо и достаточно, чтобы для любого ε>0 можно указать такое А>0, что для любых R’ и R”, превосходящих А, .

Зам. Отметим, что из сходимости несобственного интеграла не вытекает даже ограниченность подынтегральной функции. Н-р, интеграл , где функция равна 0 для нецелых x и равна n при x=n (целое число), очевидно, сходится, хотя подынтегральная функция неограниченна.

В дальнейшем мы будем считать, что функция f(x) задана на полупрямой a≤x<+∞ и для любого R≥a существует обычный интеграл . Докажем следующую теорему.

Теорема 2. (общий признак сравнения). Пусть на полупрямой a≤x<+∞ (4). Тогда из сходимости интеграла вытекает сходимость интеграла .

∆ Пусть сходится. Тогда, согласно критерию Коши, для любого ε>0 найдется такое А>0, что для любых R’>A и R”>A, выполняется неравенство . (5)

Согласно известным неравенствам для интегралов и неравенству (4) имеем

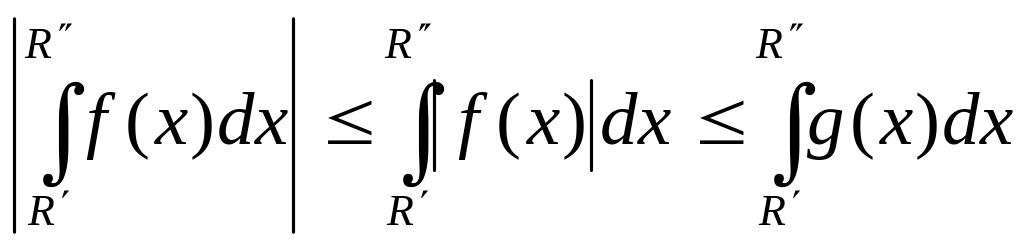. Отсюда и из неравенства (5) вытекает, что для любых R’ и R”, больших А, справедливо неравенство . Следовательно, интеграл сходится. ∆

Теорема 3. (частный признак сравнения). Пусть на полупрямой 0<a≤x<∞ функция f(x) удовлетворяет соотношению , где с и р – постоянные, р>1. Тогда интеграл сходится. Если же существует такая постоянная с>0, что на полупрямой 0<a≤x<∞ справедливо соотношение , в котором р≤1, то интеграл расходится.

Следствие (частный признак сравнения в предельной форме). Если при р>1 существует конечное предельное значение (х→+∞), то интеграл сходится. Если же р≤1 существует положительное предельное значение (x→+∞), то интеграл расходится.

Убедимся в справедливости первой части следствия. Для этого заметим, что из существования предела при x→+∞ вытекает ограниченность функции , т.е. с некоторой постоянной с₀>0 выполняется неравенство . После этого применяется первая часть теоремы 3. Справедливость второй части следствия вытекает из следующих рассуждений. Так как с>0, то можно указать столь малое ε>0, что с-ε>0. Этому ε отвечает А>0, что при х≥А выполняется неравенство с-ε< (это неравенство следует из определения предела). Поэтому и в этом случае действует вторая часть теоремы 3.

Абсолютная и условия сходимость несобственных интегралов.

Введем понятия абсолютной и условной сходимости несобственных интегралов. Пусть f(x) интегрируема по любому сегменту [a, R].

Опр.1. Несобственный интеграл наз. абсолютно сходящимся, если сходится .

Опр.2. Несобственный интеграл наз. условно сходящимся, если он сходится, а интеграл расходится.

Зам. Положив в теореме 2 g(x)=|f(x)|, мы получим, что из абсолютной сходимости несобственного интеграла вытекает его сходимость.

Отметим, что теоремы 2 и 3 позволяют установить лишь абсолютную сходимость исследуемых несобственных интегралов.

Теорема 4. (признак Дирихле – Абеля). Пусть функции f(x) и g(x) определены на полупрямой a≤x<∞. Пусть далее функция f(x) непрерывна на полупрямой a≤x<∞ и имеет на этой полупрямой ограниченную первообразную F(x). Предположим еще, что функция g(x), монотонно не возрастая a≤x<∞, стремится к нулю при х→+∞ и имеет производную g’(x), непрерывную на полупрямой a≤x<∞. При этих условиях сходится несобственный интеграл . (6)

∆ Воспользуемся критерием Коши сходимости несобственных интегралов. Предварительно проведем интегрирование по частям интеграла на произвольном сегменте [R’, R”], R”>R’, полупрямой a≤x<∞. Получим . (7)

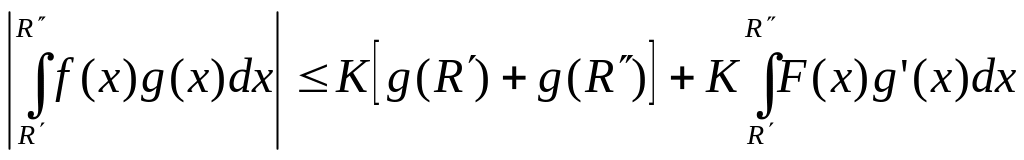По условию теоремы F(x) ограничена: . Так как g(x) не возрастает и стремится к нулю при х→+∞, то g(x)≥0, а g’(x)≤0. Таким образом, оценивая соотношение (7), мы получим следующее неравенство: . Так как интеграл в правой части этого неравенства равен g(R’)-g(R”), то, очевидно, (8).

Используя это неравенство, нетрудно завершить доказательство теоремы. Пусть ε – произвольное положительное число. Так как g(x)→0 при х→+∞, то по данному ε можно выбрать А так, чтобы при R’≥А выполняется неравенство g(R’)<ε/2K. Отсюда и из неравенства (8) следует, что для любых R’ и R”, больших А, выполняется неравенство , которое, согласно критерию Коши, гарантирует сходимость интеграла (6). ∆

Зам. Требование дифференцируемости функции g(x) в теореме 4 является излишним. Теорема 4 может быть доказана в предположении одной лишь монотонности g(x) и стремления g(x) к нулю при х→+∞.