6. Законы распределения непрерывных случайных величин

6.1. Нормальное распределение

Наиболее важным распределением непрерывных СВ является нормальное распределение. Множество явлений в практической жизни можно описать с его помощью, например, высоту деревьев, площади садовых участков, массу людей, дневную температуру и т.д. Оно используется для решения многих проблем в экономической жизни, например, число дневных продаж, число посетителей универмага в неделю, число работников в некоторой отрасли, объемы выпуска продукции на предприятии и т. д.

Нормальное распределение находит широкое применение и для аппроксимации распределения дискретных СВ, например, доходы от определенных видов рискованного бизнеса.

Нормальное распределение иногда называют законом ошибок, например, отклонения в размерах деталей от установленного.

Нормальная СВ имеет плотность распределения:

(6.1)

где | х‌‌‌<∞, а=М(Х), λ=σ(Х).

Основные свойства W(x):

а) W(x)>0 и существует при любых действительных значениях х;

б) при | х|→∞ limW(x)=0;

в) W(x=а)=W_max(x).

г) W(x) симметрична относительно прямой х=а.

д) W(x) имеет две точки перегиба, симметричные относительно прямой х=а; с абсциссами а–λ и а+λ и ординатами 1/(λ√2π).

Формула (6.1) содержит два параметра: математическое ожидание а=М(Х) и стандартное отклонение λ=σ. Существует бесконечно много нормально распределенных СВ с разными M(Х) и σ(X).

Математическое ожидание а характеризует положение кривой распределения на оси абсцисс. Изменение параметра а при неизменном σ приводит к перемещению оси симметрии (х=а) вдоль оси абсцисс и, следовательно, к соответствующему перемещению кривой распределения. М(Х)=а иногда называют центрам распределения или параметром сдвига.

Изменение среднего квадратического отклонения при фиксированном значении математического ожидания приводит к изменению формы кривой распределения. С уменьшением λ вершина кривой распределения будет подниматься, кривая будет более «островершинной». С увеличением λ кривая распределения менее островершинная и более растянута вдоль оси абсцисс.

Одновременное изменение параметров a и λ приведет к изменению и формы, и положения кривой нормального распределения.

Условимся о форме записи СВ X~D(X;М(Х),σ²), что означает: СВ X подчиняется закону распределения D с математическим ожиданием М(Х) и стандартным отклонением, либо дисперсией σ².

6.2. Стандартное (нормированное) нормальное распределение

Если в формуле (6.1) а=0; λ=1, то

= (6.2)

– стандартное (нормированное) нормальное распределение.

Стандартная нормальная СВ обозначается Z~N(X;0,1²). Оно табулировано.

Свойства функции φ(z):

а) функция ω(z) – четная, т. е. ω(z)= ω(–z);

б) при |z|→∞ W(z)→0; при |z|>5 можно считать, что ω(z)=0. В связи с этим таблицы ограничиваются аргументами z=4 или z=5;

г) максимальное значение функция ω(z) принимает при z=0.

Любая нормально распределенная СВ может быть преобразована в стандартную (нормированную) нормально распределенную СВ действием:

Z=(X-a)/ λ. (6.3)

Обратное преобразование стандартной нормальной СВ Х~N (X;a,λ²):

X=a+Z∙λ. (6.4)

6.3. Вероятность попадания в интервал нормально распределенной СВ. Интегральная функция Лапласа–Гаусса и ее свойства. Связь нормальной функции распределения с интегральной функцией Лапласа–Гаусса

Если СВ задана плотностью распределения W(x), то вероятность того, что X примет значение, принадлежащее интервалу (α, ), определяется:

P(X) .

Если СВ X~N(X; a, λ²), то

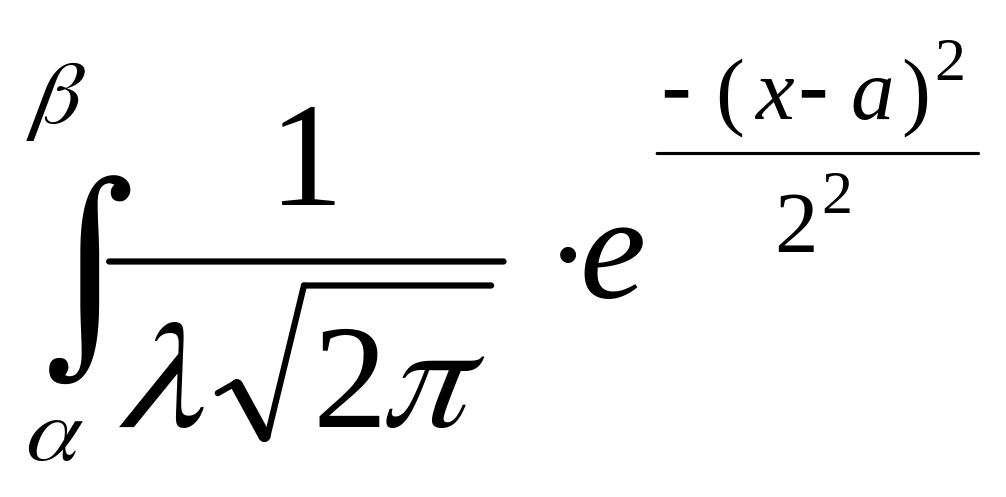P(X)= dx.

Чтобы пользоваться таблицами для вычисления вероятностей, преобразуем X в Z и найдем новые пределы интегрирования. При х=, z=(–а)/λ; при х=, z=(–а)/λ, x=a+λz, dx=λdz. Тогда

P(X)=

Функция вида

(6.5)

называется интегралом вероятностей или функцией Лапласа.

Функция Лапласа в общем виде не берется. Ее можно вычислить одним из способов численного интегрирования. Эта функция табулирована. Пользуясь функцией Лапласа, окончательно получим:

P(X)= . (6.6)

Формула (6.6) называется интегральной теоремой Лапласа.

Свойства ₀(z):

а) ₀(z) – нечетная; т.е. ₀(–z)=-₀(z);

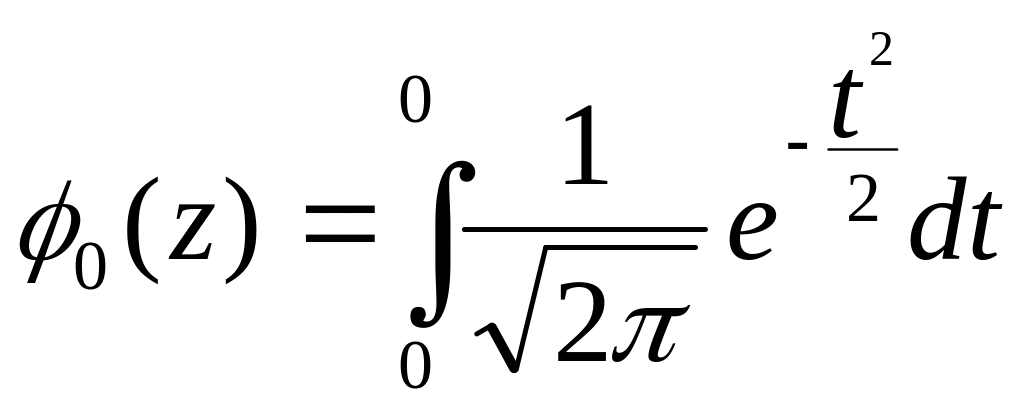б) при z=0 =0;

в) при z+∞ ₀(z) 0,5; при z–∞ ₀(z) –0,5. Ф₀(4)=0,499997,

Ф₀(–4) = –0,499997, т.е. при z4 можно считать, что Ф₀(z)±0,5.

Следовательно, все возможные значения интегральной функции Лапласа-Гаусса принадлежат интервалу (0,5; +0,5).

Итак, функция распределения СВ, подчиняющейся нормальному закону распределения, представленная через функцию Лапласа есть:

F(x)=0,5+Ф_о[(x–a)/λ]. (6.7)

Во многих ситуациях может быть рассмотрена задача обратная предыдущей: определение z по заданной вероятности попадания случайной величины в интервал.

6.4. Правило «трех сигм»

Если обозначить (X–a)/σ=Z, Δ=(X–a)=σZ, то:

P(|X–a|<Zσ)=2Ф₀(z), (6.8)

где 2Ф₀(z) – вероятность того, что отклонение СВ от ее математического ожидания М(Х)=а по абсолютной величине будет меньше z сигм.

Пусть z равно: 1; 2; 3. Пользуясь формулой (6.8) и таблицей интеграла вероятностей, вычислим вероятность того, что отклонение по абсолютной величине будет меньше σ, 2σ и Зσ:

при z=1, Δ=σ и P(|X–a|< σ)=2Ф₀(1)=0,6826;

при z=2, Δ=2σ и P(|X–a|<2σ)=2Ф₀(2)=0,9544;

при z=3, Δ=3σ и P(|X–a|<3σ)=2Ф₀(3)=0,9973.

Вероятность того, что СВ попадет в интервал (а–3σ; а+3) равна 0,9973.

Т.е. вероятность того, что отклонение СВ от математического ожидания по абсолютной величине превысит утроенное σ, очень мала и равна 0,0027. В этом состоит правило «трех сигм»: если СВ распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает ±3σ.

6.5. Понятие о теоремах, относящихся к группе «центральной предельной теоремы»

В теоремах этой группы выясняются условия, при которых возникает нормальное распределение. Общим для этих теорем является следующее: закон распределения суммы достаточно большого числа независимых СВ при некоторых условиях неограниченно приближается к нормальному.

Познакомимся с содержанием (без доказательства) с одной из теорем.

• Центральная предельная теорема для одинаково распределенных слагаемых (теорема П. Леви).

Теорема. Если независимые СВ Х₁, Х₂,… Х_n, имеют один и тот же закон распределения с математическим ожиданием а и дисперсией σ², то при неограниченном увеличении n закон распределения суммы Х₁+Х₂+…+Х_n неограниченно приближается к нормальному.

Теорема Ляпунова. Если СВ Y представляет собой сумму большого числа независимых СВ Y₁, Y₂,… Y_n, влияние каждой из которых на всю сумму равномерно мало, то величина Y имеет распределение, близкое к нормальному, и тем ближе, чем больше п.

Ценно то, что законы распределения суммируемых СВ могут быть любыми, заранее не известными исследователю. Практически данной теоремой можно пользоваться и тогда, когда речь идет о сумме сравнительно небольшого числа СВ. Опыт показывает, что при числе слагаемых около 10 закон распределения суммы близок к нормальному.

Теорема Ляпунова имеет важное практическое значение, поскольку многие СВ можно рассматривать как сумму независимых слагаемых (ошибки измерений, отклонения размеров деталей, распределение числа продаж некоторого товара, валютные курсы и т.д.)

6.6. Показательное (экспоненциальное) распределение

Экспоненциальное (показательное) распределение связано с распределением Пуассона, используемым для вычисления вероятности появления события в некоторый период времени. Распределение Пуассона – это распределение числа появления событий в заданный интервал времени длиной t. Параметр распределения Пуассона λ характеризует интенсивность процесса, с его помощью вычисляют среднее число появления события.

Например, в банк в среднем входит пять посетителей в час. Предположим теперь, что вместо числа появления события в заданный промежуток времени нас интересует длина промежутка времени до появления первого посетителя в банке. Такая задача решается при помощи экспоненциального распределения, а не распределения Пуассона.

Другие примеры. Интервалы времени до первого телефонного звонка на станцию, время ожидания такси – подчиняются экспоненциальному закону.

Обозначив среднее значение появления событий в некоторый промежуток времени через λ, а время до появления первого события х=t, можно получить дифференциальную функцию экспоненциального распределения:

(6.9)

где х0, λ>0 – параметр. Функция экспоненциального закона:

. (6.10)

Числовые характеристики экспоненциально распределенной СВ X: М(Х)=1/λ, D(x)=1/λ²,(x)=1/λ.

6.7. Закон равномерного распределения (равномерной плотности)

Если известно, что значения непрерывной СВ принадлежат определенному интервалу, а ее плотность распределения на интервале постоянна, то СВ распределена по равномерному закону.

В равномерном распределении вероятность того, что СВ будет принимать значения внутри заданного интервала, пропорциональна длине этого интервала.

Пусть непрерывная СВ X распределена на интервале (α;β) с равномерной плотностью. Ее плотность W(х) на этом участке постоянна и равна C. Вне этого интервала она равна нулю, так как СВ X за пределами интервала (α; β) значений не имеет. Найдем значение постоянной С. Площадь, ограниченная кривой плотности распределения вероятностей и осью абсцисс, должна быть равна единице, т.е. С(β–α)=1.

Следовательно, С=1/(β–α) и плотность для равномерного распределения:

(6.14)

Функция распределения (6.15)

Числовые характеристики равномерно распределенной СВ: М(Х)=(α+β)/2, D(x)=(β–α)²/12, (x)=√D(x)=(β–α)/2√3.

Для непрерывной равномерно распределенной СВ X, заданной на интервале (a<X<b)

P(a<X<b)=(b–a)/(β–α). (6.19)